🛠️ステートマシンミーリムーア　DFAとNFA DFSM NFSM GNFA STS NPDA DPDA

あたり帳簿

2020年12月3日 05:54

DFA (決定性有限オートマトン)：決定性有限オートマトンは、ある状態から別の状態への遷移が一意的に決まる有限オートマトンです。つまり、同じ状態から出る複数の遷移が同じ記号でラベル付けされることはありません。

NFA (非決定性有限オートマトン)：非決定性有限オートマトンは、ある状態から複数の遷移が同じ記号でラベル付けされ、その結果、複数の可能な次の状態が存在する可能性がある有限オートマトンです。

DFSM (決定性有限状態マシン)：これはDFAと同義語です。つまり、ある状態から別の状態への遷移が一意的に決まる有限状態マシンです。

NFSM (非決定性有限状態マシン)：これはNFAと同義語です。つまり、ある状態から複数の遷移が同じ記号でラベル付けされる有限状態マシンです。

GNFA (一般化非決定性有限オートマトン)：一般化非決定性有限オートマトンは、遷移が正規表現でラベル付けされる非決定性有限オートマトンです。

STS (状態遷移システム)：状態遷移システムは、システムが一連の状態を通じて進化する方法をモデル化する数学的モデルです。

NPDA (非決定性プッシュダウンオートマトン)：非決定性プッシュダウンオートマトンは、スタックというデータ構造を使用して非決定性の遷移を行うオートマトンです。

DPDA (決定性プッシュダウンオートマトン)：決定性プッシュダウンオートマトンは、スタックというデータ構造を使用して決定性の遷移を行うオートマトンです。

ステートマシーンという言葉がある

正規表現はオートマトンと密接な関係があるのをしったのはこの本の冒頭だった。

https://amzn.to/2HO4Kc6

ここにミーリやらムーアNFA、DFAもろもろ説明がのっている。

そしてこの本にboyer-moore法というのが出てきて、このムーアとムーアマシンは関係があるのだろうかとおもっていた。

このアルゴリズムでは検索文字列（パターン）の前処理を行い、検索対象テキストの前処理は行わない。したがって、テキストについて何度も検索を行わない場合に適している（他のアルゴリズムではテキスト側に前処理を施し、繰り返し検索を行うことで前処理のコストを償却する）。テキスト上の全文字をチェックする必要はなく、前処理で得た情報を活用してスキップしながら処理していく。一般にパターン文字列が長いほど検索が高速化される。検索文字列とテキストの間での不一致が発生するたびに、不一致であったという情報を最大限に利用して照合しなくてもいい位置を可能な限り排除することで、効率を向上させている。

なんと、関係がなかった！どうしよう

boyer-moore法は分かりやすかったのに、まじめにDFA/NFAのことを調べよう。

任意のNFAには、それと同じ言語を受容する決定性有限オートマトン（DFA）が存在する。実用的なオートマトンを得るために、しばしばNFAはDFAに変換される。

正規表現の起源は、言語学と、理論計算機科学の一分野であるオートマトン理論や形式言語理論にみることができる。20世紀の言語学では数理的に言語を扱う数理言語学が発展しその過程の一部として、また後者は計算のモデル化（オートマトン）や形式言語の分類方法などを扱う学術分野である。数学者のスティーヴン・クリーネは1950年代に正規集合と呼ばれる独自の数学的表記法を用い、これらの分野のモデルを記述した。

サブリニアランタイムアルゴリズムは、ボイヤー・ムーア（BM）ベースのアルゴリズムと、リバーススキャンなどの関連するDFA最適化技術を用いて達成されています。

関係あるのかな

幅広い種類のPOSIX構文と拡張をサポートするGNU grepは、ファーストパスの前処理にBMを使用し、その後暗黙のDFAを使用します。近似マッチングを実装しているWu agrepは、BDM(backward DAWG matching)で前処理をDFAに結合している。NR-grepのBNDMは、BDMの技術をShift-Orビットレベルの並列性で拡張したものです。

前処理としてBMが使われ、受け皿としてDFAがあるということのようだ。(無関係ではなかった)NFAがDFAに変換されるということなので、DFAの形をいくつか見てみるか。

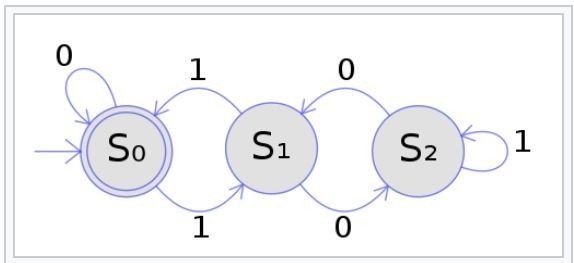
3の倍数の2進数のみを受け入れる決定論的有限オートマトンの例。状態S0は開始状態であり、受け入れ状態でもある。例えば、文字列 "1001" は、状態列 S0, S1, S2, S1, S0 につながり、したがって、受け入れられる。

分かるような分からんような。。。。

整理する

オートマトン業界で出てくる用語を整理してみたい

DFA決定性有限オートマトン（けっていせいゆうげんオートマトン、英: Deterministic Finite Automaton）aka.決定性有限状態機械（けっていせいゆうげんじょうたいきかい、英: Deterministic Finite State Machine）aka.DFSM
NFA 非決定性有限オートマトン[1]（ひけっていせいゆうげん-、英: Nondeterministic Finite Automaton）aka.非決定性有限状態機械（ひけっていせいゆうげんじょうたいきかい、英: Nondeterministic Finite State Machine）aka.NFSM
拡張非決定性有限オートマトンaka.GNFA
状態遷移系（じょうたいせんいけい、State Transition System）aka.STS

さらに条件を拾っていく

任意のNFAにはれと同じ言語を受容するDFAが存在する。実用的なオートマトンを得るために、しばしばNFAはDFAに変換される。
DFA や NFAは簡単に GNFA に変換でき、GNFAは正規表現に簡単に変換できる。

NFA→DFA→GNFA→正規表現

有限オートマトン(FA・FSM)
　決定的有限オートマトン (Deterministic Finite Automata (DFA))
　非決定的有限オートマトン (Nondeterministic Finite Automata (NFA))
　ε動作を含む非決定的有限オートマトン (Nondeterministic Finite Automata, with ε transitions (FND-ε,ε-NFA))
　ムーアマシン
　ミーリマシン

無限オートマトンというのは議論には出てこないので、チューリングマシン一番意味が広くて、それに近いかつ決定的か非決定論的な強さにはあんまり関わらないが、有限というところで計算力の問題が出てくるみたいだった。そんな議論の中で出てくるのが「非決定性プッシュダウン・オートマトン」（NPDA）だ

有限オートマトンでも特に非決定性有限オートマトン(NFA)に基づいている場合、「非決定性プッシュダウン・オートマトン」（NPDA）と呼ばれる。決定性有限オートマトン(DFA)に基づいている場合、「決定性プッシュダウン・オートマトン（英語版）」（DPDA）と呼ばれる。非決定性とは、入力信号と状態とスタック上の文字を与えられても次の遷移先が一意に決定されない場合があることを意味する。

有限オートマトンにふたつのスタックを接続することもでき、これは事実上チューリングマシンと等価な非常に強力なデバイスとなる。線形拘束オートマトンはプッシュダウン・オートマトンよりも強力だが、チューリングマシンよりは非力である。　

DFAの図にもどって「決定」とは何かを振り返る

図は、状態図を用いた決定論的有限オートマトン（DFA）を示しています。この例のオートマトンでは、3つの状態がある。S0, S1, S2 の 3 つの状態がある（丸印）。このオートマトンは、0 と 1 の有限シーケンスを入力とする。シンボルを読み取ると、DFA は遷移矢印に沿って、ある状態から別の状態へと決定論的にジャンプします。

決定論的にジャンプ。

オートマトン（自動機械）には自律して動いては欲しいが、機械に気ままに動かれるといろいろな事情で困るわけで、含みとしてDeterministic Finiteというくくりが出てくる。実際のハードウェアもそのように作り出される。

量子ビットで選択肢が爆上がりもしくは極小電力かつ何億同時並行になったとしてもロジックがＤＦだったら透明性から少し安心はできる。

「決定論的に」は若干食い気味で言ってみてほしい。

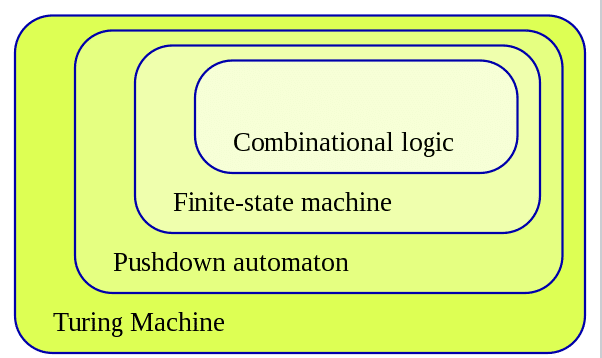
有限状態機械は、チューリング機械などの他の計算モデルよりも計算力が低い。計算力の違いは、チューリング機械にはできて、FSMにはできない計算タスクがあることを意味する。これは、FSMのメモリが状態の数によって制限されるためです。

https://en.wikipedia.org/wiki/Finite-state_machine

ステートマシンと呼ばれる回転式改札機には、2つの状態がある。ロック状態とロック解除状態である[4] 。その状態に影響を与える入力は、コインを投入すること（コイン）とアームを押すこと（プッシュ）の2つである。ロック状態では、アームを押しても何の効果もなく、何度プッシュという入力を与えられてもロック状態のままである。コインを入れる、つまりコインの入力を与えると、ロック状態からアンロック状態に移行する。ロック解除の状態では、コインを追加投入しても効果はない。つまり、コインを追加投入しても状態は変わらない。しかし、顧客がアームを押して、プッシュ入力を与えると、状態はロックされた状態に戻る。

https://en.wikipedia.org/wiki/Finite-state_machine

決定論（けっていろん、英: determinism、羅: determinare）とは、あらゆる出来事は、その出来事に先行する出来事のみによって決定している、とする哲学的な立場。

https://ja.wikipedia.org/wiki/%E6%B1%BA%E5%AE%9A%E8%AB%96

バックトラッキング

バックトラッキングとNFA（非決定性有限オートマトン）およびDFA（決定性有限オートマトン）との間には関連性があります。特に正規表現エンジンのコンテキストでこの関連性が顕著です。

バックトラッキング:
- バックトラッキングは、多くの正規表現マッチングエンジンで使用されるアルゴリズムの一部です。
- 特に「貪欲な」マッチやキャプチャグループ、前方/後方参照などの高度な正規表現の機能をサポートするエンジンでは、マッチングの過程で複数の選択肢が存在する場合、一つの選択肢を探索した後で別の選択肢に戻る必要があります。これがバックトラッキングです。
- バックトラッキングを多用する正規表現エンジンは、特定の入力やパターンで非常に遅くなることがあります。
NFA:
- NFAは非決定性を持つため、複数の遷移先が存在する可能性があります。この非決定性は、バックトラッキングのアイディアと一致しています。つまり、一つの選択肢を探索した後、別の選択肢に戻ることができます。
- そのため、多くのバックトラッキングを使用する正規表現エンジンは、内部的にNFAベースのアプローチを採用しています。
DFA:
- DFAは決定性を持ち、ある状態からの特定の入力に対して一つの明確な遷移先しか存在しません。
- そのため、DFAはバックトラッキングを必要とせず、入力を一度だけスキャンしてマッチングを判定することができます。
- しかし、NFAをDFAに変換する際に状態の数が指数関数的に増加する可能性があり、メモリ消費が問題となることがあります。

結論として、バックトラッキングとNFA/DFAは正規表現のマッチングのコンテキストで密接に関連しています。NFAベースのエンジンはバックトラッキングを使用する可能性が高く、DFAベースのエンジンはバックトラッキングを必要としません。

NFAとDFAのような関係を持つ事物や概念は、多くの分野に存在します。具体的には、複数の可能性や選択肢から一つの決定的な結果や形に絞り込むというプロセスを示すものです。以下はそのような関係を持つ事物や概念の例です。

量子力学と古典力学:
- 量子力学は確率的な現象を扱うのに対し、古典力学はより決定論的な現象を扱います。量子系がマクロスコピックなスケールになると、古典的な振る舞いに収束します。
確率的アルゴリズムと決定論的アルゴリズム:
- 確率的アルゴリズムは、ある確率で正しい答えを返すか、または計算の各ステップでランダムな選択を行います。一方、決定論的アルゴリズムは常に同じ入力に対して同じ出力を返します。
ブレインストーミングと意思決定:
- ブレインストーミングでは、さまざまなアイディアや解決策を自由に提案します。これに対し、意思決定のプロセスでは、提案されたアイディアの中から最も適切なものを選び出します。

これらの例は、多くの選択肢や可能性から一つの結果や答えを選び出すという点で、NFAとDFAの関係に似ています。

いいなと思ったら応援しよう！

お願い致します

🛠️ステートマシン ミーリ ムーア DFAとNFA DFSM NFSM GNFA STS NPDA DPDA