仮想数学史:会円術の先にあったかもしれない数学
北宋末期の人である沈括(1031〜1095)が会円の術と呼んでいる近似計算法がある。ここの"会"は、集める、集まるの意味で、直訳すれば"円を集める術"ということになるが、意味不明だろう。
これは、任意の角度で切り取られた円弧の弧長を"矢"の長さから計算する方法を与える。円弧の角度を$${\theta}$$、半径を$${R}$$とした時、矢の長さとは$${R(1-\cos \dfrac{\theta}{2})}$$のことで、弧の長さは当然$${R \theta}$$であるから、現代的には、逆三角関数の計算を与えているものと読める。
少し面白いことに、矢長と弧長の(近似)関係式は代数的に与えられているので、代数方程式を解くことで弧長から矢長を計算することもできた。この計算法は、授時暦でも使われたそうだ。
夢溪筆談 卷十八技藝で該当箇所を抜粋すると以下の部分。
履畝之法,方圓曲直盡矣,未有會圓之術。凡圓田,既能拆之,須使會之復圓。古法惟以中破圓法拆之,其失有及三倍者。
雑訳:履畝(土地測量)の法では、方・円・曲・直なんでも求められるが、會圓(会円)の術がまだない。円田は、分割した後でも、集めて円に戻すことができる。古法では、中破圓法で、これを分割したが、その誤差は3倍(?)にもなることがあった(弧長を折れ線近似で求めることを言ってるらしい)。
餘別為拆會之術,置圓田,徑半之以為弦,又以半徑減去所割數,餘者為股;各自乘,以股除弦,餘者開方除為勾,倍之為割田之直徑。以所割之數自乘倍之,又以圓徑除所得,加入直徑,為割田之弧。
雑訳:余は別途、拆會の術を作った。円田があって、その半径を斜辺とし、また、半径から"分割した数"(矢の長さのことらしい)を引いたものを股(直角三角形の斜辺でない辺の一方)となす。それぞれ二乗し、斜辺(の二乗)から股(の二乗)を引き、平方根を取って、勾(直角三角形の残りの一辺)を出す。2倍すると、田の"直徑"(円弧の弦のこと)が出る。矢の長さの二乗の2倍を、円の直径で割り、弦の長さを加えると、弧長となる。
文で書くとわかりにくいが、円の"直径"と呼んでる弦長は、$${2 R \sin(\theta /2)}$$に相当するから、
$${ \dfrac{ 2 (R(1- \cos (\frac{\theta}{2})))^2 }{2 R} + 2R \sin( \frac{\theta}{2} ) \approx R \theta }$$
ということになる。全体を$${R}$$で割って
$${ \theta \approx 2 \sin (\frac{\theta}{2} ) + (1 - \cos(\dfrac{\theta}{2}) )^2 }$$
となる。$${x = \dfrac{\theta}{2} }$$と置く。円弧の中心角$${\theta}$$が、0度から180度の範囲だと考えてたなら、$${ 0 \leq x \leq \dfrac{\pi}{2} }$$で、
$${ x \approx \sin(x) + \dfrac{1}{2}(1 - \cos x)^2 }$$
となる。
$${x = \mathrm{arccos}(y)}$$とすれば
$${x = \mathrm{arccos}(y) \approx \sqrt{1-y^2} + \dfrac{1}{2} (1-y)^2 }$$
となって、逆三角関数の代数的近似を与えている。
沈括は、この式をどうやって得たか詳しい説明をしてないが、九章算術にある公式から導出されたものと思われている。九章算術 方田の章に以下の2問がある。
今有弧田,弦三十步,矢十五步。問為田幾何?
答曰:一畝九十七步半。
又有弧田,弦七十八步、二分步之一,矢十三步、九分步之七。問為田幾何?
答曰:二畝一百五十五步、八十一分步之五十六。
術曰:以弦乘矢,矢又自乘,并之,二而一。
前者は、弦長が矢長の2倍であることに気付けば、半円の面積を計算するだけの問題で、円周率を3とすれば、答えを得る(一畝=240平方歩)
後者の問題は、それほど綺麗な中心角を持たない。中心角を$${ \theta (\mathrm{rad}) }$$で、半径を$${R}$$の円弧を考える時、"術"が言ってるのは、弓形(円弧と弦で囲まれた部分)の面積に対する近似計算法であり、現代の記号で書けば、
$$
\pi R^2 \dfrac{\theta}{2 \pi} - R^2 \sin \dfrac{\theta}{2} \cos \dfrac{\theta}{2} \approx \dfrac{1}{2} R^2(1- \cos \dfrac{\theta}{2})^2 + R^2 \sin \dfrac{\theta}{2} (1-\cos \dfrac{\theta}{2})
$$
となる。少し変形すれば、沈括の公式と同値であることが分かる。
沈括の公式を、試しに$${ x \approx \sin(x) + \dfrac{1}{2}(1 - \cos x)^2 }$$の両辺をプロットしてみると、一見すると、そこまで悪い近似でもない。
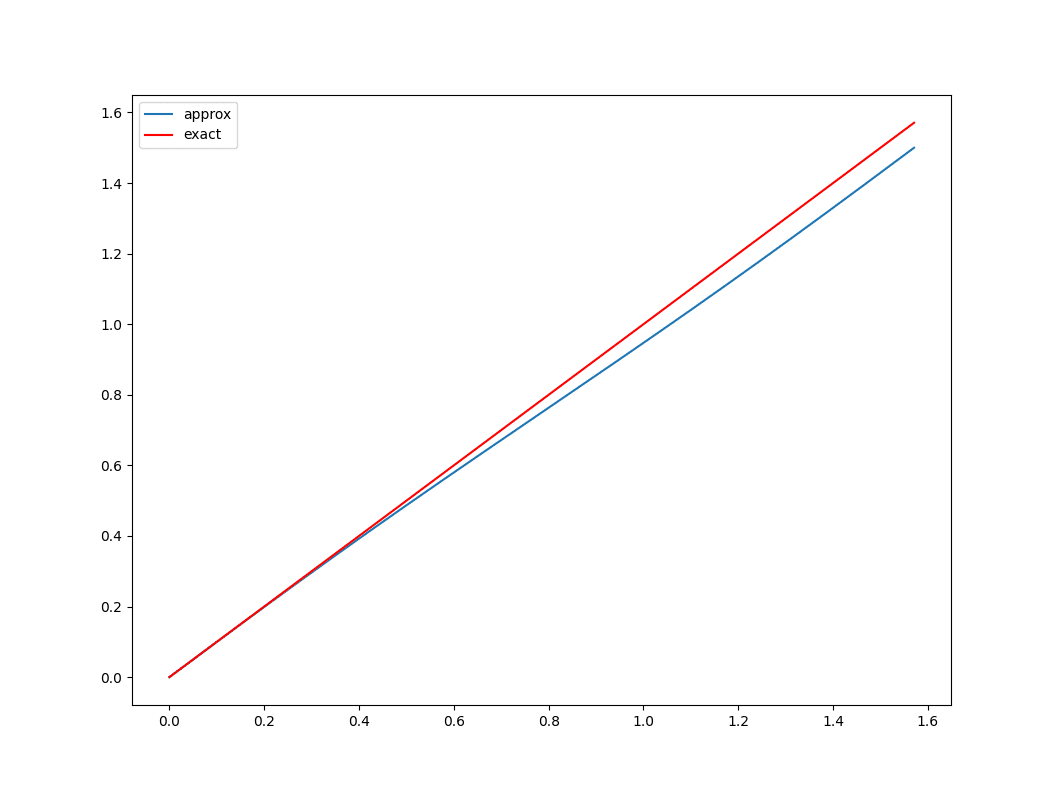
もっと広い範囲で見ると以下の通り。

$${0 \leq x \leq \dfrac{\pi}{2} }$$の範囲で、最も誤差が大きいのは、$${x=\dfrac{\pi}{2}}$$の場合で、$${ \dfrac{\pi - 3}{2} }$$になる。
九章算術のの元々の公式がどうやって得られたのか定かでないが、半円の問題で円周率を3と近似してたことから考えて、沈括の近似式は
$${ \dfrac{3}{\pi} x \approx \sin(x) + \dfrac{1}{2}(1 - \cos x)^2 }$$
と解釈する方がより正確かもしれない。プロットしてみると、円周率が3の時と真値の時で、最大誤差はあまり変わらず5%程度になるが、平均的な誤差は、円周率が3として計算した弧長との方が小さく、1%を下回る。

ところで、
$${ x \approx \sin(x) + \dfrac{1}{2}(1 - \cos x)^2 }$$
は、高校数学の知識で少し書き直すと
$${x \approx \dfrac{3}{4} + \sin(x) - \cos(x) + \dfrac{1}{4} \cos(2 x) }$$
となる。こうしてみると、なんかフーリエ級数のように見えてこなくもない。
$${x \approx p_{0} + p_{1} \sin(x) + p_{2} \cos(x) + p_{3} \cos(2 x) }$$
で近似した時、最良の係数$${p_{0},p_{1},p_{2},p_{3}}$$は何だろうか
答えは、勿論、"最良"をどう定義するかによって変わる。
その前に、この式で、$${x=0,\pi/2}$$の時、両辺が厳密に等しいとすると
$${p_{0}+p_{2}+p_{3} = 0}$$
$${p_{0} + p_{1} - p_{3} = \dfrac{\pi}{2}}$$
また、この近似式を一度微分すると
$${ 1 \approx p_{1} \cos(x) - p_{2} \sin(x) -2 p_{3} \sin(2x) }$$
で、$${x=0,\pi/2}$$の時、両辺が厳密に等しいとすると、$${p_{1}={1},p_{2}=-1}$$を得る。
以上を解くと、係数$${p_{0},p_{1},p_{2},p_{3}}$$が決定できて
$${p_{0}=\dfrac{\pi}{4} , p_{1}= 1 , p_{2} =-1 , p_{3}=1 - \dfrac{\pi}{4}}$$
を得る。円周率を3と置くと、沈括の近似式が再現される。
沈括が、こんな方法を使ったとは思えないが、一応、それなりの根拠を与えられた。
もっといい係数を決めるための最良の一つの基準は、
$${ I = \displaystyle \int_{0}^{\pi/2} \left( x - (p_{0} + p_{1} \sin(x)+ p_{2} \cos(x) + p_{3} \cos(2 x)) \right)^2 }$$
を最小化するというもの(L2ノルムが最小)。発想としては、最小二乗法と同じ。係数$${ p_0,p_1,p_2,p_3 }$$の計算には
$${ \dfrac{\partial I}{\partial p_{0}} = \dfrac{\partial I}{\partial p_{1}} = \dfrac{\partial I}{\partial p_{2}} = \dfrac{\partial I}{\partial p_{3}} =0}$$
とやって、これは連立一次方程式なので、普通に解けばいい。手でやれなくはないが、計算機にやってもらう。
import sympy
p0,p1,p2,p3,x = sympy.symbols("p0,p1,p2,p3,x")
I0 = (x-p0-p1*sympy.sin(x)-p2*sympy.cos(x)-p3*sympy.cos(2*x))**2
I=sympy.integrate(sympy.expand(I0), (x,0,sympy.pi/2))
M= sympy.zeros(4,4)
v = sympy.zeros(1,4)
for n in range(4):
v[n] = -sympy.diff(I, [p0,p1,p2,p3][n]).subs([[p0,0],[p1,0],[p2,0],[p3,0]])
for m in range(4):
M[n,m] = sympy.diff(sympy.diff(I , [p0,p1,p2,p3][n]),[p0,p1,p2,p3][m])
w=sympy.simplify(M.inv()*(v.T))
print(w)
print(w.evalf())以下のように出力される。
Matrix([[pi/4], [3*(-3pi**2 - 8 + 12pi)/(-18pi - 32 + 9pi2)], [3*(-12pi + 8 + 3pi2)/(-18pi - 32 + 9pi2)], [6*(-22 + 7pi)/(-9pi2 + 32 + 18*pi)]])
Matrix([[0.785398163397448], [0.975246138589144], [-0.975246138589144], [0.191194860633730]])沈括の係数と大きくは変わらないが、最も差が大きくなる時で、0.00135未満(沈括の場合は、0.070796・・・)
"最良近似"の別の考え方は、最大誤差が最も小さいという条件(一様ノルム最小化)。上の係数では、0.00135未満だが、もっと小さく出来るだろうか。理論的に出す方法は多分ないので、数値最適化に頼る
import numpy as np
import scipy.optimize
xs = np.arange(0,5000+1)*np.pi/10000
def test(p):
ys = p[0]+p[1]*np.sin(xs)+p[2]*np.cos(xs)+p[3]*np.cos(2*xs)
return np.max(np.abs(xs-ys))
res = scipy.optimize.minimize(test , np.array([0.75,1,-1,0.25]) , method="SLSQP",tol=1.0e-12)
print(res.x)[ 0.78540317 0.97946356 -0.97947237 0.19473437]という出力を得る。最大誤差は、0.0006651685967181409
差をプロットすると、以下のようになる。
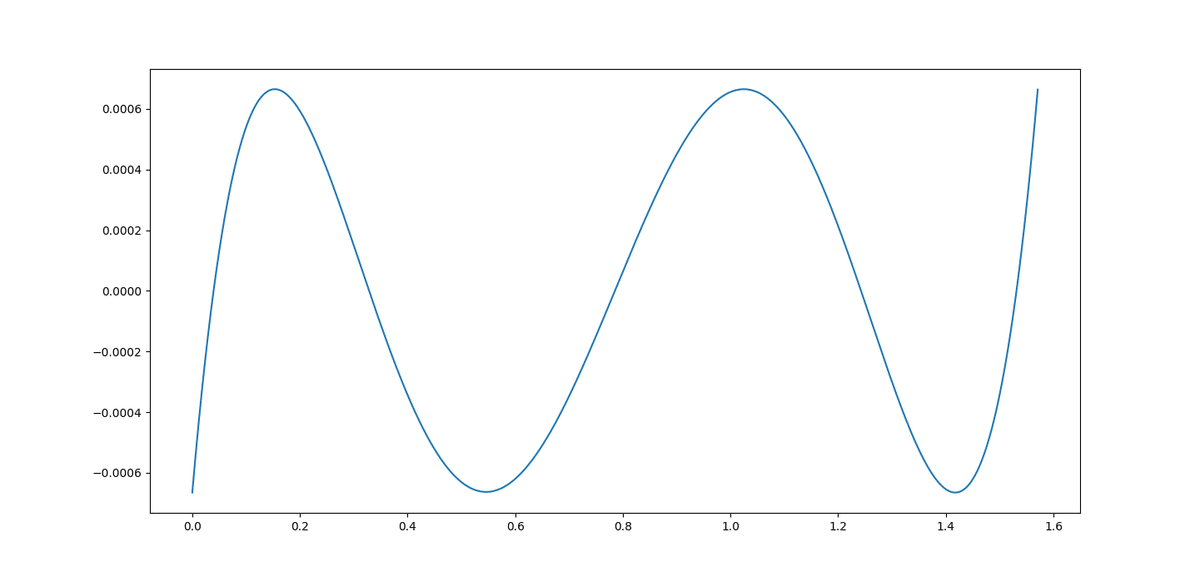
$${x=0}$$の時は、$${0}$$になってほしい気もするので、拘束条件を課して最適化してみる。
res = scipy.optimize.minimize(test , np.array([0.75,1,-1,0.25]) , method="SLSQP",tol=1.0e-12,constraints=[{'type':'eq' , 'fun':lambda p:p[0]+p[2]+p[3]}])
print(res.x)出力は、[ 0.78349408, 0.98245241, -0.97928249, 0.19578841]で、最大誤差は0.0009589073382156588で、誤差のプロットは以下の通り。

沈括が、積分したり、微分して極値を求めるという発想を持つのは無理だったろうが、
$${x \approx p_{0} + p_{1} \sin(x) + p_{2} \cos(x) + p_{3} \cos(2 x) }$$
という近似式で、より良い係数を探すというのは、突拍子もない発想とも言えない。何百点もサンプリングして数値最適化するのは無理だが、$${x=n \pi/8 (n=0,1,2,3,4)}$$程度の点数で最適化するだけでも、そこそこの数値は出る。
この5点で数値最適化すると、[ 0.78539802 0.98041476 -0.98041453 0.19501648]という係数が得られた。これは沈括よりは、良い近似を与える。どうやって極値を求めるかさえ気付けば、4変数の連立方程式を解くことは、元代の中国人数学者には可能だった。
仮に、何らかの方法で係数を決めたとして、この方法で、sin関数を計算すると、どのくらいの精度があっただろう。$${v = \sin(x)}$$とすると
$${x \approx p_{0} + p_{1} v + p_{2} \sqrt{1-v^2} + p_{3} (1-2v^2) }$$
の解$${v}$$を計算すれば、$${\sin(x)}$$が計算できるという次第。一様ノルム最小化で得た最大誤差で、0.0006651685967181409など。
プトレマイオスは、アルゲストで、"弦の表"を与え、数表から線形補間で、"三角関数"(正確には$${2 \sin(\theta/2)}$$に相当する量)を計算しようとした。
$${ \sin(x) \approx \dfrac{1}{2}( \sin(x+\epsilon) + \sin(x-\epsilon)) = \sin(x) \cos(\epsilon) }$$
で、アルマゲストの数表の刻み幅は、sin関数として見ると、0.25度刻みに相当したので、誤差は、最大で$${1-\cos(0.125^{\circ})}$$程度で、最大でも、$${10^{-5}}$$から$${10^{-6}}$$のオーダー。
従って、計算量を考えても、代数方程式を毎回解くのは大変すぎるが、最大限頑張っても、アルマゲストの精度にすら勝てないという結果になる。
