
“バカ”が国立大に受かるには
はじめに
はじめましてのみなさん
私は30を迎えるただのおっさんになってしまいました
まわりでは同年代の人たちが
子供をもつ家庭をつくったり、結婚したりしています
そんななか自分は結婚の「け」の字もないような生活を送っています
発信する主な理由は
その同年代たちの子供たちの世代が
自分の苦労したことに関しては、知識として身につけ
苦労はすることなく乗り越えていってほしいと思っているからです
自分が苦労して作ったわずかな人生のレシピのようなものを共有したいと思っています
もちろん今を生きる同年代、それ以上、それ以下の人たちの少しででもお役に立てれば幸いです
同年代たちの子供たちが生きていくのに少しでも「楽」になるように
所帯をもったり、親になったりした
同年代たちのひとたちが生きていくのに少しでも「楽」になるように
そして一生「勉強」を続けていけるように
今回のように「受験」に関しても、扱えるところは扱います
少しくさいですが
人生の塾のような、学校のような、令和の寺子屋のようなものをできたらなと思っています
youtubeでもしゃべろうと思っているので
noteは文字の媒体として残すのと、youtubeでしゃべる内容のたたき上げのようなものです
またこの記事については主に受験勉強について書かれたものです
妹が高校受験を迎えるにあたって、これを機に
彼女が苦しむことなく受験を乗り越えたらなと思って書きました
同年代の方々はお酒を片手にでも
受験勉強の種明かしのひとつです
なにかを勉強するときのきっかけにモチベーションになれば幸いです
受験生のみなさんへ
後述にあるとおり、受験勉強に関していうと
ある程度、過去問に触れるようになってからの話が書いてあります
絶対数に対しての多くの受験生にとっての最大の関門は
過去問に触れるようになるまでの
全教科、全単元を一通りさらう完成度と時間になることは理解していますが
youtubeにもたくさん動画が上がってますし
とりあえずはなんとか頑張ってください
ただ受験情報をネットで探しているようなあなたなら、そこらへんはクリアできていることでしょう
すぐに取り組めるのは、浪人生と、一通りのことが終わっている比較的優秀な高校の現役生かと思われます
また内容は大学受験に関してですが
高校受験とも大きく違わないので高校受験にもよくいえるはなしだと思っています
タイトルについて
まずはじめに“バカ”とは何か
国立大とはどこの大学を想定しているかを書きます
帰納と演繹 と “頭がいい”と”バカ”
自分はこういうとき帰納と演繹と表現するんですが
なんとなく数学の帰納法と演繹法を思い浮かべてもらえるといいと思います
帰納的にできるとは、最初から原理的に理解できることを意味していて
たとえば”教科書がよめる”ような人のことです
少し抽象的に書かれた原理や原則を理解して、具体的な事例や問題にうまくあてはめて解決、理解できるような人たちのことです
こういうような人たちのことを”頭がいい”と表現しています
一方で演繹的にしかできないとは、(帰納的にできなく)最初から原理的に理解できない、つまり具体的な個々の事例をいくつか(いくつも)やってようやく原理的に理解することしかできない”教科書がよめない”ようなやつを”バカ”としています
まさに自分がその”バカ”のひとりです
”頭がいい”人たちも参考になれば、受験勉強に割く時間と労力が減るので
ほかの有意義なことに使ってください
受験勉強はそれなりの時間と労力、気力を割く必要があると思っていますが
それは努力すべきであり、苦しむ必要は全くないと思っています
単に「受験勉強」ができるだけで、いわゆる「国内トップ」の大学にいける
これは非常にくだらないことだと思っていますが、私たち“バカ”にとっては非常に幸運であり、ありがたいことだと思っています。
“バカ”でも努力さえすれば「国内トップ」”ちょっと下”の大学にいけると思ってるのでこれを書いています
これは演繹的に受験勉強を努力して乗りきるためのnoteです
ただし演繹的にしかできない人間が、頑張って帰納的に、演繹的な手段を説明しようとしているので読みにくいところがあるかもしれませんがご笑納ください
国立大
基本的に東大、京大を除いた旧帝大を指していて
名古屋大学、東北大学、北海道大学、大阪大学、九州大学…
クラスを想定してます
ただし自分の受験情報は10年前ですので
(大阪大学)、名古屋大学、東北大学、九州大学、(北海道大学)...の国立
といった感じでしょうか
(大阪大学)としたのは自分の頃は名古屋、東北と大差はなく
数学だけはひとくせあったような印象でしたが
10年前に比べて偏差値があがった敬意をこめて
(北海道大学)としたのはゲームが違いました
共通試験(センター)の上位互換です
問題数が多い、そこそこの難易度の問題の中での、完成度の勝負です
医学部は100%近く求められました
その傾向自体は変わってはないとは思いますが
繰り返すように自分の10年前の受験情報ですので
知らんけど、程度です。
なんでこうも国立と言っているのかは、主なメリットは2つ
休学が無料なこと と 学費に対しての予算が比較的潤沢だということです
個人的には大学院には必ずしも行く必要がなく
1~2年の休学を含めて、5~6年かけて学部を卒業するのがいいのではないかと思ってます
ですので私大のように休学期間中に学費の一部以上を払わなくちゃいけないのは大きいと感じています
またたしかに研究室によるところもありますが
学費が安い割には、研究資金が潤沢にあります
実験設備や機器、研究(室)環境はベターと言えるでしょう
まれに歴史的に古いため老朽化が激しい建物などがある場合もありますが例外といっていいでしょう
「受験勉強」
なにを解くか? 過去問
圧倒的に過去問一択!!
過去問が圧倒的に問題としての質が高く、完成されいて、面白いです
それもそのはず、優秀な教授陣を始めとする研究者たちが人員、時間をかけて作ってくれた問題です
多くの問題集は過去問を改変したものであって
どこまでいっても参考書程度と思った方がいいでしょう
なので旺文社発行の入試問題正解をどうにかして手に入れてください
高校受験をそれなりにやった方々なら記憶にあるでしょう
年度ごとの全国の国公立、有名私立の載ったあのオレンジ色のばかに分厚い過去問集です
大学受験の場合は教科別に分かれているためそんなに分厚くはないのですが
教科ごと入手しなければいけないので自分で買うのはおすすめしません
自分の場合は高校の進路相談室にありましたが、図書室に依頼するか、
入試問題正解のためだけに塾、予備校を最低限のコマだけで契約するのも手かもしれません
どうにかして入試問題正解を手に入れるのが非常に重要です
どう解くか? 問題作成者の意図を解く
問題作成者の意図を解く、これに尽きます
(どこかの動画でQKの伊沢拓子も「林修もそう言ってる」と言ってました)
自分自身、昔から「国語」が苦手でした
原理的に、論理的に、根本的に作品を読み解くことから問題を解こうとしてたんですけど、どう頑張っても非常にやりにくかった
大学受験を迎えて
数学、理科(物理、化学)全てを原理的に、論理的に、根本的に問題を解くのも理解しようとするのも、とっくのとうに限界でした
根本的な理解から問題を解こうとするといくつかの解法、アプローチが見えてくるんですけど、そのどれを選ぶべきかも分からないし、その解法それぞれの道筋、ゴールも、全体は見えないし明確にも見えません
原理的に、根本的に理解しようとしても、全教科、全単元に対してしようとすると膨大な時間と労力が必要でとても無理でした
自分とその問題となる題材との間で、論理的に、根本的に理解することでおのずと問題の正解が出てくると思っていたんですけど
どうやらそうすると沼にはまっちゃうんです

そこでどうやっても「理解」できない国語をどうにかしようとしてる時に気が付いたんですけど
どういう意図でこの問題が作られて
どういう過程で解かれることが想定されているのか
そう考えるとなんとか腑には落ちる
題材と問題の間に「問題作成者」という人間がいて、その問題を解くことができればいいんだと

問題やその題材と直接ではなく
単に問題作成者との対話を丁寧にすればよかったのだと分かりました
そしてこれが意外にも数学、理科(物理、化学)や他の教科にも当てはまる
ここまでくれば、受験勉強はクソゲー、やりゲー
あとはいかにくだらないことをクソ真面目にできるか
知的好奇心、自己肯定感(一般的にまわりから短絡的に評価される)を高められるだけましなクソゲー、やりゲーです
ご存知の通り、京大には通用しにくいですがそこに至る過程までなら有効だと思っています
また東大レベルでも通用しないことはないと思っているんですが
いかんせん努力でどうにもならない人がいる可能性もあります
一番は自分が自ら東大レベルまではやれなかったというところが大きいです
具体的には
まずはちゃっちゃと過去問に進んじゃってください
Twitterで浪人生が整数、自然数の定義をきっちりノートに書いて
おれでもこんなことやってる(すごいだろ)的な人がいましたけど
寒気がしました
定義、原則まで立ち返ることはたしかに重要ですが
そのこと自体はなんの目的にもなりません
浪人生や、一通り終わった現役生は過去問にすすみましょう
目安は知らない単元はほとんど無い、やったことがない、全く知らない単元が無いってとこまでで十分でしょう
数学だと巷ではチャート何周やってからなんていわれたりもしてますが
どこまでいっても完成することはないんで
そして多くの場合完成度の上限もたかが知れているので
最低限サーっと1周さえすればいいと思います
分からなかったらバンバン解答をみましょう
苦手な単元は無理せず中途半端な完成度で全くかまいません
いきなり試験問題まるまるやってもかまわないですけど
無理そうだったなら最初は1つの大問ごとにやっていくんでもかまいません
解けなさそうだったら解答はどんどん見ましょう
そして解答を読み込んで、問題と解答を行ったり来たり
問題作成者がどういう風に解答することを想定しているのか
またこの問題はどういう意図で構成されているのか
選択肢だったら、その選択肢のひとつひとつに意味があり、意図があります
なぜこういう選択肢をつくり、どうやって正解を選ばせようとしているのか
そんなことを考えながら、自分で選択肢を考えることもできます
基本的に1時間かけて解く問題は、解答を読み込んで周辺知識を埋めていってなどやっていたら最大で3時間、1 ~ 3倍ほどの時間がかかると思います
過去問をさわりながら分からなかったりしたら
また教科書に、参考書に立ち返りましょう
その都度、抜けていたら基本に立ち返り
周辺の知識を肉付けしていくようなイメージです
苦手な分野だったら参考書の問題を少し多くやってみるなど
そのときに少しだけ力を入れてやってみたらいいんじゃないでしょうか
実際に問題でどういう理解の仕方を求められているのか
そういったことからその分野、単元での理解する切り口が見えてくると思います
また問題作成者の意図が追えると、数をこなしていると
分野、単元に対しての見方も変わってくると思います
あぁ、この分野はこういう理解の仕方が求められていて
こういう問題の出方がよくあるよなぁ、とか
自分が問題つくるならこういった構成で、こういう聞き方をするかなぁ
などと違った視点、角度からとらえられるようになっているはずです
またよくいわれることですが
こういった理解できないものが、理解できるようになるときは
線形に、比例するような形でじわじわと徐々に理解できるようなものではなく、

経験のある方々なら分かるとは思いますが、理解度は想像以上に非線形に変化することがよくあります
指数関数的にあるところから急激に理解がすすむこともあれば

右側線点線は時間に対しての理解度の変化は急激に大きくなる
全く変化がなかったところから
階段的に急にワンステップ理解がすすむ場合もあります
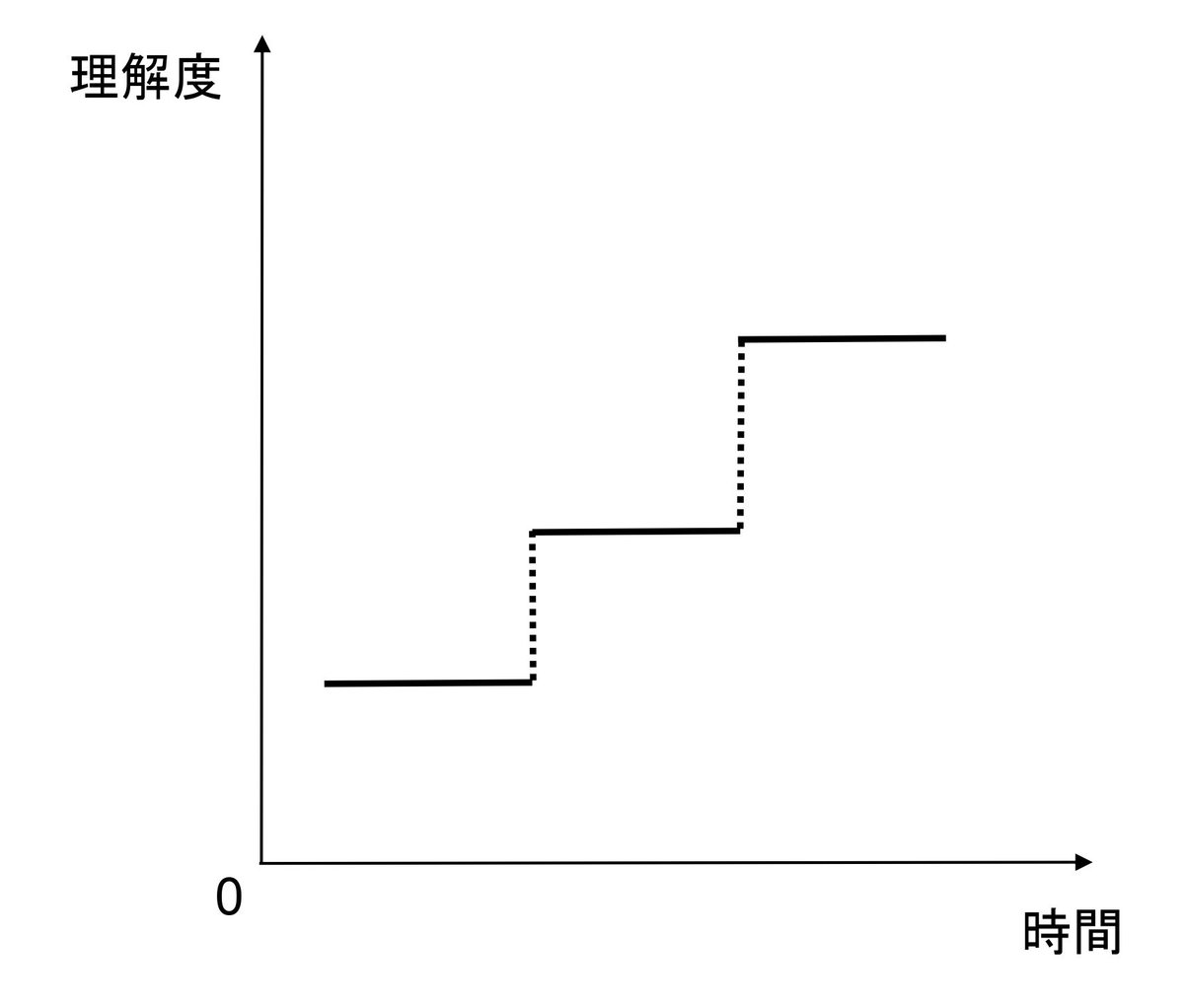
理解できなかったのが噓のように
こう、ガッチャンっと
ですので怖がらずに一緒にすすみましょう
(私もこれを読んでくれている立派な大人たちも一緒にすすみます)
報われるタイミングは来るはずです
つらくないですか?
そもそもなんでこんな方法をすすめてるのかというと
やみくもに受験勉強するのってつらくないですか?
一般的なやりかたを想像してみると
とりあえず教科書とかを開きながら参考書やら、問題集をやっていきますよね
これがそもそもけっこうつらくないですか?
分かったんだか、分かってないんだか
進んだんだか、進んでないんだか
やってて意味があるのか、効果があるのか
今日、確かにやるにはやったけども
“何をやったか”をきかれると
何をやったのか自分でもよくわからないし
どこまでできたのかも自信がないし
そんなことが分からないことを続けるのって
つらくないですか?
しかも状況が状況で
趣味でやってて時間がほぼ無限にあるってわけでもなく
だいたい1年以内に試験日というゴールが迫っているなか
どれだけ焦らないようにしても焦ってしまうのが人間だと思います
それに合わせて、やっぱりちょっと過去問やってみようかな
なんて触ってみると、全く解けずに
またさらに焦って"やっぱりまだまだ力が足りてないんだ”
なんて思っちゃったりしませんか?
こんなことは続かなくて当たり前でいいと思ってます
だからもうある程度のところで切り上げて
過去問にすすんじゃって
解けなくていいんです
解答を読み込んでそれなりに理解ができれば
数をやっているうちに見えてくることもあるんです
やりゲー、クソゲーだといいましたが
要はこうやってしまえば
クオリティの高い過去問と、それなりの解答をなんども反芻していけば
攻略サイト、攻略本がある
やりゲー、クソゲーだってことです
そうすればやってて分からないことに関してはほとんどないはずです
その分野だったり、周辺知識を入れようとするときに
まだ理解の甘いところだったり
分からないようなことはあるかもしれませんが
こと、今やっている問題に関していえば
ほとんどのことが理解できるはずです
今日やったことは、少なくとも
ここの問題を理解できたと、具体的にいえるはずです
さらにいえばここの分野の内容はだいたいここくらいまで復習、理解できたな、なんてことも言えるかもしれません
毎回やっていること、その日やったことが
具体的に自信をもって把握でき
着実に、一歩一歩すすんでいることが分かるでしょう
さらに攻略サイト、攻略本をなぞって進めばいいので
(過去問と解答の反復)
ほとんどストレスなく進めるでしょう
ほら、なんだか
あとは単にどこまでやるかだけだな、と思えて来ませんか
マップの隅々までどれだけ丁寧に、深く周って
キャラクターをいかに最強にできるかだけなんです
補足
勉強に関しての方法論的なことはこれで終わりですが
せっかく「受かるには」とタイトルをうったので
少しだけ戦略的な話もしようと思います
志望校
志望校の設定はとりあえず「東大志望」をおすすめします
いちおう「東大志望」と周りに言えるくらいがいいということです
理系、文系の分類自体が好きじゃないんですけど
理系でも、国語は(社会も)当たり前に落とせない
共通試験(センター)ならなおさら
文系でも、数学は(理科も)当たり前に落とせない
共通試験(センター)ならなおさら
そこから最終的に(大阪大学)、名古屋大学、東北大学、九州大学、(北海道大学)...の国立へ
というのがいいと思います
圧倒的に共通試験(センター)の点数が落とせないので
合格者平均以上は当たり前にとれるはずです
勉強時間
苦しんでほしくない、苦労しないでほしいと再三書いてきましたが
それなりの努力は絶対に必要です
それなりの時間、気力、体力を割かないことにははじまりません
考えてみてください、私たちより優秀な人たちと戦うんですよ
彼らは同じ問題を私たちより短い時間で、より真面目に、より少ない労力でこなせます
なので私たちが手を抜ける理由は一切ありません
ですのでおすすめの方法は
基本的に「24時間」受験勉強に割くということです
24時間勉強しろと言っているのではなく
24時間を受験勉強(のパフォーマンス)を最大(効率)化するために費やす
ということです
たとえば睡眠時間は10時間とり、昼寝を1時間弱
1日のスケジュールを考えてみると
21:00 ~ 22:00 就寝
7:00 起床 勉強開始
10:00 朝食
10:30 ~ 11:00 勉強再開
13:00 ~ 14:30 くらいの間に1時間ほど昼食兼休憩
(遅くても)15:30 ~ 勉強再開
(昼寝 1時間弱)
19:00 ~ 20:00 夕食
寝るまで勉強再開
21:00 ~ 22:00 就寝
のようなものです
個人的には単に勉強時間を最大化させようとするのはナンセンスだと思っています
勉強時間の最大化は当然の結果であって
勉強時間の最大化は(手段にならなりうるかもしれないですが)目的ではありません
今回は少し特殊で、手段と目的が混同してますが
(なるべくなら本来の目的、その達成の手段、それによる結果をそれぞれ意識したほうがいいけども)
目的(のひとつ)は間違いなく受験合格であって、その手段、目的のひとつとして勉強(すること)の最大化になるはずです
その結果、勉強時間はおのずと最大化されます
ですので睡眠時間はしっかり確保してください
休息をとることもれっきとした受験勉強です
積極的な休養をとってください
何かのパフォーマンスを最大化するために戦略として休養をとるんです
なのでこのスケジュールの中に運動をする時間を設けるだとか
趣味の時間をつくるなんてこともとても大切です
よくありますが勉強時間をつけるくらいなら
勉強しなかった時間をつけた方がよっぽど有意義だと思っています
おわりに
拙い文章でしたが読んでいただきありがとうございました
推敲は続け文章は改善していくつもりです
またトッピクごとにnoteを分けて書くなどもやっていきます
また記事だけでなく
youtubeも収益化が叶えばメンバーシップをつくり
一部の有料化を考えております
そんなたいそうなことではなく
岸田奈美さんと岡田斗司夫の有料的な考えで
見つけ次第、張りたいんですが
岸田奈美さんがnoteに有料記事を書きだすことに関しての記事がどこかにあったんですが
そこで佐渡島庸平さんに面白い方を無料にして、つまらない方を有料にしなよって言われているようなやつがあったんですよ
それを参考にします
また岡田斗司夫はジブリの解説が分かりやすい例だと思うんですが
絶対的に面白い!みたいな考察、解説のような内容は無料できっちりやって
ちょっとまだ本人の中でも曖昧だったり、すこし踏み込んで自分の想像、妄想を交えた仮定の話みたいなものを有料にしてるんですよね
なのでその2つにならって大トロの一番おいしい部分は無料で
ちょっとまだ咀嚼しきれてないような不完全なものを有料にしていくようなことを考えております
面白いので岸田さんはぜひ
面白すぎるので公共交通機関で読むことはおすすめしません
爆笑できる環境でぜひ読んでみてください
