なぜ政府支出伸び率と名目成長率の間には強い相関があるのか?
政府支出伸び率と名目成長率の間にある強い相関の謎について研究してみました。
1. 論争を呼ぶグラフ
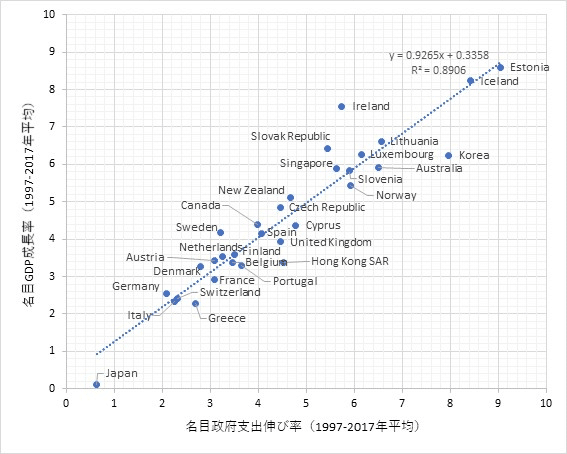
出発点は、こちらのグラフを巡る論争です。このグラフは、1997年から2017年にかけての名目政府支出伸び率と名目GDP成長率を年平均で示したものです。両者の間には決定係数0.8906という強い相関があり、また、$${x}$$の係数は0.9265となっており、「名目支出伸び率≒名目GDP成長率」という関係が成り立っています。
この相関関係はどのようにして生じているのでしょうか? 両者の間に因果関係はあるのでしょうか? 因果関係があるとすれば、どのような因果関係があるのでしょうか?
2. 2つの仮説
このグラフを巡っては、大きく2つの仮説が対立しています。
仮説1:政府支出が増えれば名目GDPが増える
仮説2:名目GDPが増えれば政府支出が増える
仮説1が正しければ、政府支出を意図的に増やしていくことで名目成長を促すことができることになります。
しかし、仮説1に反対する人は、名目GDPが増えると税収が増え、結果政府支出を増やすことができただけだと考えています。つまり、政府支出を意図的に増やしても名目成長を促すことはできないという主張です。
どちらの主張が正しいのでしょうか。
私の考えは、「どちらの仮説も正しい面があり、現実には双方向の因果関係となっている。ただし、仮説1は構造的な因果関係であり、仮説2は裁量的な因果関係である」というものです。
裁量的な因果関係というのは、次のようなことです。
税収が増えたからと言って政府支出を増やすかどうかは政府の裁量次第であり、税収が増えた分を減税や債務の償還に用いる可能性がある
名目GDPが増えなくても増税や国債発行によって政府支出を増やす可能性がある
これだけの裁量の余地があってなお、両者に強い相関があるということは、仮説2以外の何らかのメカニズムが働いていると考えざるを得ないのではないでしょうか。
ということで、ここからは仮説1「政府支出が増えれば名目GDPが増える」が成り立つのかどうかを検証していきます。
3. 前提
仮説1が成り立つためには、次の2つの前提が必要となります。
前提1:政府が赤字を出す(負債を増やす)とお金の量が増える
前提2:お金の量が増えると名目GDPが増える
前提1はMMT(現代貨幣理論)の主張から導かれる帰結です。会計的整合性の観点から基本的に正しいと言えますが、一応「前提」としておきます。
なぜ前提1が正しいのかということについては、こちらの動画で図を使いながら説明しています。
前提2は、言い換えると「お金の量から独立して名目GDPが決まるのではない」ということです。政府が赤字を出すということは、民間が黒字になるということです。民間が黒字になるということは、誰かの所得が増えるということです。よって、前提2は、「限界消費性向が0ではない」と表現することもできます。つまり、「所得が増えた時に誰も消費を増やさないということはあり得ない」ということを前提とします。
前提2が正しいかどうかについては、最後にもう一度検討するとして、ここからは2つの前提が成り立つと仮定した場合の帰結を考えていくことにします。
4. 名目GDPと政府支出の関係
4.1. 政府債務残高と政府支出・税収の関係
まず、このような関係を考えてみましょう。
$$
\dfrac{\Delta{M_g}}{\Delta{t}}=G-T\tag{1}
$$
$${M_g}$$は政府債務残高を表し、$${t}$$は時間(年)を表しています。$${\dfrac{\Delta{M_g}}{\Delta{t}}}$$はある期間における政府債務残高の増加額(年額換算※)を表し、$${G}$$はある期間の政府支出(年額換算)を、$${T}$$はある期間の税収(年額換算)を表しています。
※「年額換算」というのは、そのままのペースで債務を増やし(あるいは支出/徴税し)続ければ1年間で○○円になるという意味です。
また、前提1より、$${M_g}$$は「政府がこれまでに増やしたお金の残高」という意味でもあります。政府支出と税収の差額分だけ、「政府が増やしたお金」の残高は増えていくことになります。
数式(1)は、$${G}$$と$${T}$$が$${M_g}$$に占める割合をそれぞれ「政府支出率」$${S}$$と「徴税率」$${R}$$とすることで、次のように変形することもできます。
$$
\dfrac{\Delta{M_g}}{\Delta{t}}=(S-R)M_g\tag{2}
$$
このとき、$${S-R}$$は$${M_g}$$の伸び率を意味します。
$${\Delta{t}}$$の長さは$${\Delta{t}=1}$$(1年)とすることもできますし、$${\Delta{t}=\dfrac{1}{12}}$$(1ヶ月)とすることも、$${\Delta{t}=\dfrac{1}{365}}$$(1日)とすることもできます。そして、$${\Delta{t}}$$を限りなく短い時間とすると、次のように表すことができます。
$$
\lim_{\Delta{t}\to0}\dfrac{\Delta{M_g}}{\Delta{t}}=M_g'=G-T\tag{3}
$$
4.2. 名目GDPと政府債務残高の関係
この時、ある時点における「瞬間的な名目GDP(年額換算)」というものを想定し、これを$${Y}$$とします。そして、マネーストック$${M}$$が$${M_g}$$の何倍になっているかを「信用倍率」$${c=\dfrac{M}{M_g}}$$、マネーストックが年に平均何回使われるかを「貨幣流通速度」$${V=\dfrac{Y}{M}}$$で表すことにすると、次の数式が成り立ちます。
$$
\\Y=VcM_g\tag{4}
$$
なお、以後$${Vc}$$セットで1つの変数として扱います。このとき、$${Vc}$$は「政府が増やしたお金」の利用率を意味します。この$${Vc}$$概念については、「経済の活性度」の指標として活用できる可能性があると考えています。詳しくはこちらの記事をご覧ください。
4.3. 名目成長率と政府支出伸び率
ここでは、政府支出を一定の伸び率$${g}$$で増加させ続けた場合に、名目成長率$${y}$$がどのような値に収束するかを考えたいと思います。なお、徴税率$${R=\dfrac{T}{M_g}}$$は一定とし、$${Vc}$$の影響を受けないものとします。
仮定1:Rは一定で、Vcの影響を受けない
実際の$${R}$$は中長期的に変動し、とりわけ$${Vc}$$との間に強い正の相関があります。そのため、仮定1はやや非現実的なものです。そこで、後ほどこの仮定は現実に近付ける形で修正を試みます。
以上の想定の下で、$${G}$$および$${T}$$は次のように表すことができます。なお、$${G_0}$$は$${G}$$の初期値です。
$$
G=G_0e^{gt}\tag{5}
$$
$$
T=RM_g\tag{6}
$$
これらを数式(3)に代入すると、次の微分方程式が得られます。
$$
M_g'=G_0e^{gt}-RM_g\tag{7}
$$
この微分方程式を解くと、$${C}$$を積分定数として、次の式が得られます。
$$
M_g=\dfrac{G_0e^{gt}}{g+R}+\dfrac{C}{e^{Rt}}\tag{8}
$$
$${t=0}$$の時の$${M_g}$$を$${M_{g0}}$$とすると、$${C}$$は次の式で表すことができます。
$$
C=M_{g0}-\dfrac{G_0}{g+R}\tag{9}
$$
$${S=\dfrac{G}{M_g}}$$より(8)(9)を用いることで、次の式が得られます。なお、$${S_0=\dfrac{G_0}{M_{g0}}}$$は$${S}$$の初期値です。
$$
S=\dfrac{g+R}{1+\dfrac{g+R-S_0}{S_0e^{(g+R)t}}}\tag{10}
$$
$${S}$$の極限を取ると、$${g+R}$$となります。
$$
\lim_{t\to\infty}S=g+R\tag{11}
$$
よって、$${M_g}$$の伸び率$${m=S-R}$$は$${g}$$に収束します。
$$
\lim_{t\to\infty}m=g\tag{12}
$$
また、数式(4)より$${Vc}$$の伸び率を$${v}$$とすると、名目成長率$${y}$$は$${m+v}$$で表すことができます。
$$
y=m+v\tag{13}
$$
ここからは場合分けをして考えていきます。
①「$${Vc}$$一定」ならば、$${v=0}$$であるため、名目成長率$${y}$$は政府支出伸び率$${g}$$に収束します。
$$
\lim_{t\to\infty}y=g\tag{14}
$$
②「$${Vc}$$が周期的な変動をする」ならば、$${Y}$$の平均伸び率$${\bar{y}}$$は政府支出伸び率$${g}$$に収束します。
$$
\lim_{t\to\infty}\bar{y}=g\tag{15}
$$
③「$${Vc}$$が定率で増加/減少し続ける」ならば、$${y}$$は$${g+v}$$に収束します。
$$
\lim_{t\to\infty}y=g+v\tag{16}
$$
4.4. 仮定1の修正
4.3.では、徴税率$${R=\dfrac{T}{M_g}}$$は一定とし、$${Vc}$$の影響を受けないものとしました。これは非現実的な仮定であり、実際の$${R}$$は$${Vc}$$との間に強い正の相関があります。
よって、数式(7)は、次のように修正する必要があります。
$$
M_g'=G_0e^{gt}-rVcM_g\tag{17}
$$
ここで、$${r}$$は$${Y=VcM_g}$$に対する税収の割合、すなわち付加価値に対する税率と考えることができます。
なお、この数式を解析的にすっきりと解くことができなかったため、理論的な考察にとどめたいと思います。
$${Vc}$$が増加基調にあるとき、$${T}$$は増加し、$${M_g}$$の増加を抑制します。逆に、$${Vc}$$が減少基調にあるとき、$${T}$$は減少し、$${M_g}$$の増加を促進します。
①「$${Vc}$$一定」の場合、結論は変わりません。
②「$${Vc}$$が周期的な変動をする」場合も、おそらく結論は変わらないと思われます。解析的に解ける可能性もあるので、この点は要検証。
③「$${Vc}$$が定率で増加/減少し続ける」場合、結果はよりマイルドになると思われます。$${|\hat{v}|\lt{|v|}}$$として、
$$
\lim_{t\to\infty}y=g+\hat{v}\tag{18}
$$
すなわち、実際にはより$${g}$$に近い数値に収束すると思われます。こちらはシミュレーションなどで要検証。
5. 考察
5.1. 前提は正しいか?
結論に入る前に、改めて2つの前提について検討しておきましょう。
前提1:政府が赤字を出す(負債を増やす)とお金の量が増える
前提2:お金の量が増えると名目GDPが増える
前提1については、大枠としての正しさはほぼ疑いを入れる余地のないものであると考えています。ただし、現実のデータに当てはめる場合に、いくつか問題が生じる可能性があります。この点については後ほど検討します。
前提2については、見解が分かれるところでしょう。「名目GDPはお金の量から独立して決まる」と考えている人は多いと思われます。一方で、「限界消費性向は0である」ということに同意する人は少ないでしょう。「所得が増えた時に誰も消費を増やさないということはあり得ない」という考えが正しいとすれば、前提2も正しいということになります。
逆に言えば、前提2を否定するためには、「限界消費性向は0である」という主張をする必要があります。それができない限りは、前提2が正しいと考えることには一定の妥当性があるでしょう。
5.2. 結局のところグラフをどう解釈すれば良いのか?
それでは、2つの前提が正しいとした場合、なぜ名目GDP成長率と政府支出伸び率の間には強い相関があるのか? という問いについて、どのような答えを出すことができるでしょうか。
仮説1:政府支出が増えれば名目GDPが増える
仮説2:名目GDPが増えれば政府支出が増える
2つの前提が正しいとすれば、少なくとも名目成長率$${y}$$が政府支出伸び率$${g}$$付近に収束する作用が多少なりとも発生するということになります。その場合、仮説1は少なくとも部分的には正しいということになり、仮説1を全否定することはできなくなります。
このことは、仮説2が誤っているということを意味するものではありません。上で述べたように、私の考えは、「どちらの仮説も正しい面があり、現実には双方向の因果関係となっている。ただし、仮説1は構造的な因果関係であり、仮説2は裁量的な因果関係である」というものです。
双方向の因果関係が働いており、しかも仮説1に関しては、$${y}$$が$${g}$$に「収束」するという強い関係があるのであれば、あれだけの強い相関が見られることも不思議ではありません。
6. 今後の課題とか
6.1. 前提1の課題
「前提1:政府が赤字を出す(負債を増やす)とお金の量が増える」が正しいとしても、現実のデータをモデルに当てはめる場合にはいくつか問題が生じる可能性があります。
対外収支をどのように扱うのか?
海外も含めて「民間」とするのか?
対外収支をモデルに組み込むのか?
何を$${M_g}$$とするのか?
総負債なのか純負債なのか国債残高なのか?
一般政府なのか中央政府なのか?
第1の論点については、現時点では海外も含めて「民間」とし、全ての影響を$${Vc}$$に閉じ込める戦略を取ろうと考えています。その場合、「何が$${Vc}$$を変化させるのか?」という問いを軸に経済を考えていくことになるでしょう。
第2の論点については、「中央政府純負債」を用いるのが適切であるように思えますが、慎重な検討が必要となります。また、国際比較を行うのであれば、データソースの制約から、「一般政府」の指標を使わざるを得ないと思われます。
6.2. 前提2の課題
「前提2:お金の量が増えると名目GDPが増える」については、まだ自覚できていないものも含めて、更に多くの課題があると思われます。とはいえ、「仮説1:政府支出が増えれば名目GDPが増える」を否定するためには、必ず前提2を否定する必要があります(※)。前提2が正しいか誤りかどうかというのが、今後の議論の焦点となるのは間違いないでしょう。
※もちろん、前提1を否定する手もありますが、おそらく無理だと思います。
6.3. モデルの改善
モデルについては当然のことながら、まだまだ改善の余地が多々あります。特に、「仮定1:Rは一定で、Vcの影響を受けない」を置かずにすっきりとした解を示すことが大きな課題です。
加えて、$${g}$$が変動し、$${Vc}$$も変動するような状況を想定した時に、何らかの形で$${y}$$の$${g}$$への「収束」を示すことができれば、より強く「仮説1:政府支出が増えれば名目GDPが増える」を主張できることになります。
これらの点については、$${Y}$$と$${G}$$それぞれの平均伸び率$${\bar{y}}$$と$${\bar{g}}$$の関係を考えることで解決できるのではないかと考えています。
