
1:2:√3のパズル(2)
先週の記事は、Kawadaさんのパズルを解きましたっていうものでした。
とても良いパズルだったので、ついでにその仲間のパズル「Diamond:ひし型」にも、思わず挑戦してしまいました。そんなお話をします。
このDiamond(ひし型)も、やっぱり1:2:√3の直角三角形を基本ユニットとして利用していました。
・・・・・ちょと気付きにくいように工夫されていましたけど。
この作品は、超・スーパー・エクストリームな「パズル作家」さんが、数学的考察を駆使して創作したパズルに違いないです。
こんな複雑なピース分割を、なんとなくひらめきで・・・・とか、神の啓示があったので・・・とかの理由で創出できるはずがありません。
絶対に数学の図形問題を駆使して創作したはずです。
ラジくまるは、このパズル問題を見ただけで、そこまでぴしっと判別できるにも関わらず、残念なことに「数学はできる人だが、デキル・までで止まっちゃってる人」なのです。
従って、自分でこういうパズルを作れるほどの、すぐれた数学力がありません。実にもったいない話で、本人はとっても悔しいです。
ともかく、このパズルもなかなかにむつかしかったです。良い作品です。おみごとですKawadaさん。
というわけで、Diamondはこのようなピース構成です。

このパズルのパズルピースは全てが「1:2:√3」の直角三角形単位で構成されています。でも、パズルピース構成がちょっといじわるです。
説明を端折りますが、下の図に再掲載した3個のピースは、辺の長さは「1:2:√3」を守っているのに「面積」については「単位面積」を守っていない「特殊ピース」になっています。
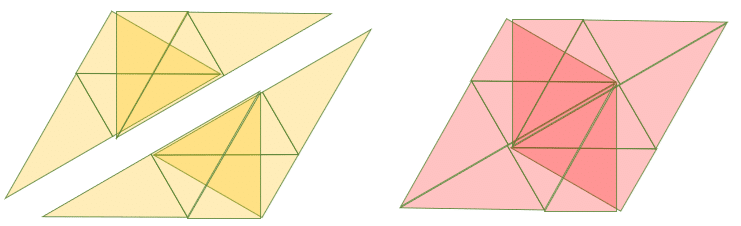
「周囲の長さの割には、面積が小さめ」になっています。
他のパズルピースとは「性質が異なり、扱いがむつかしい」のです。
こいつらは、本来あるべき姿?・期待される面積量?よりも(√3/2)くらいにちょっと小さめの面積になっています。
こういう「特例」たちが混じっているのはとても迷惑です。これら3個のせいで、かなり難しいパズルになってしまうのです。
さて、気を取り直して解析作業に戻りましょう。
買ったばかりの初期状態ではこうなっています。
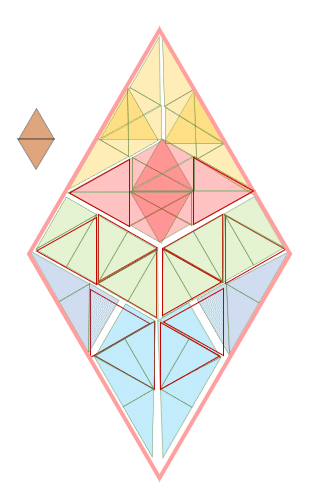
赤い三角形の「基本グリッド」を描き込んでみると、図のように基本のグリッドが並んでいることが見て取れます。
その一方で、下の図はラジくまるが挑戦してみた一例です。

でも、小さなダイヤのピースはちゃんと入ってますよ
この「惜しい?」っていう状況に、基本グリッド(赤の正三角形)を描き入れてみると、初期配置の時と比べて、基本グリッドの向きが90°回転していることがわかります。
これが惜しい組み合わせだというのですから、基本的な考え方はコレで合っているにちがいないです。つまり、グリッド(赤の三角形)はこの向きに配列するのが正解に違いないのです。
パズルピースにはそれぞれ、基本グリッドの境界線にぴったり沿って置かれるべき辺があります。それを示します。

上の図で赤い線の部分は、正解の時には赤の正三角形で図示した基本グリッド線に平行な方向になるはずです。
さらに、図で描くとこういう意味だよ、というのをお示ししておきます。
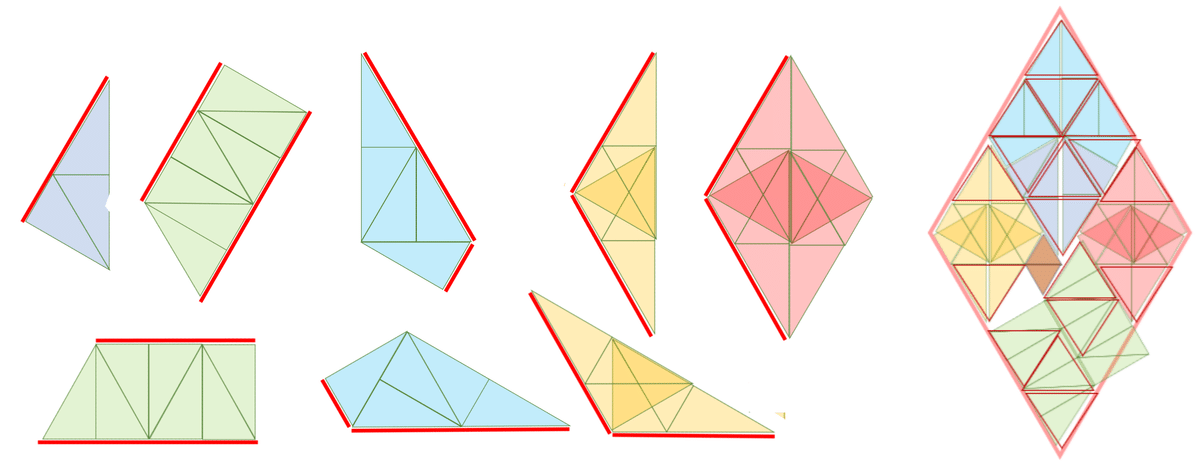
このあと、いくつかの紆余曲折があってから、ラジくまるはついに正解に至ることができました。これもすごいパズルでした。素晴らしいです。
***
ここまでの解説文を読んだ読者さまへ。
これはもう、Kawadaのパズルを購入して、自分で解いてみるしかないですよね?
ちなみに、正三角形>ダイヤモンド>正方形の順で難しかったなと感じました。
いいなと思ったら応援しよう!

