平均ランク メジアンランク モードランクの解説と推定精度の比較【累積分布関数の計算】
はじめに
今回は、累積分布関数の計算に使用される平均ランク、メジアンランク、モードランクについて解説します。
例えば確率紙を用いた推定では、得られた観測値を小さい順にならべ、横軸に観測値、縦軸にその観測値に対応する累積分布関数の値(または累積分布関数の値を用いて計算した値)をプロットします。この際、累積分布関数の値の計算方法として、主に上記の3通りが存在します。
この3通りの計算方法については、累積分布関数の値自体を確率変数として、その期待値を用いるのが平均(ミーン)ランク、中央値を用いるのがメジアンランク、最頻値を用いるのがモードランクとなります。
ワイブル分布の確率紙によるパラメータの推定においては、簡易シミュレーションの結果、総合的にメジアンランクを使用するの最も良いという結果になります。
概要
以下のように確率変数を定義します。
確率変数 $${X_{1},\ ...\ ,X_{n}}$$ は互いに独立に同一の確率分布に従い、その確率密度関数を $${f(x)}$$、累積分布関数を $${F(x)}$$ とする
$${X_{(1)},\ ...\ ,X_{(n)}}$$ を $${X_{1},\ ...\ ,X_{n}}$$ の順序統計量とする。
$${\big(X_{(i)}}$$ は $${X_{1},\ ...\ ,X_{n}}$$ の中で $${i}$$ 番目に小さい確率変数$${\big)}$$
$${X_{(i)}}$$ の累積分布関数の値 $${F(X_{(i)})=Y_{i}}$$ を確率変数として考えると、$${Y_{i}}$$ は $${Beta(i,n+1-i)}$$ に従います。これを利用することにより、累積分布関数 $${Y_{i}}$$ の推定において、主として以下の3通りに分けられます。
$${Y_{i}}$$ の期待値を用いる平均ランク $${=\footnotesize{ \dfrac{i}{n+1}}}$$
$${Y_{i}}$$ の中央値を用いるメジアンランク $${\approx\footnotesize{\dfrac{i-0.3}{n+0.4}}}$$
$${Y_{i}}$$ の最頻値を用いるモードランク $${=\footnotesize{\dfrac{i-1}{n-1}}}$$
中央値については、解析的に解くことができないため、近似式を使用します。上式 2. は Benard の近似式です。
まず、上3式の導出をします。
各方式の計算式は以下の順で導出します。
[1] $${X_{(i)}}$$ の確率密度関数 $${f_{X_{(i)}}({x_{(i)}})}$$
[2] $${Y_{i}=F(X_{(i)})}$$ の確率分布 ($${i}$$ 番目に小さい確率変数の累積分布関数の従う確率分布)
[3] $${Y_{(i)}}$$の期待値、最頻値、中央値
次に、ワイブル分布の確率紙によるパラメータの推定方法を例にとり、Pythonを使用した簡易シミュレーションにより各方式を比較します。結果としては、ワイブル分布の確率紙による推定では、メジアンランクが最適です。メジアンランクについては真の値を使用するのが最もよいですが、Benardの近似式を用いてもほとんど違いがありません。
詳細は[4]をご覧ください
最後に、今回使用したPythonのソースコードを記載します。[5] を参照ください。
[1] 順序統計量 X(i) の確率密度関数
まず、順序統計量 $${X_{(i)}}$$ の確率密度関数 $${f_{X_{(i)}}({x_{(i)}})}$$ を導出します。
順序統計量ではない $${X_{i}}$$ について、以下の条件を満たす確率を求めます。
$$
\left\{\begin{aligned}
X_{1},\ ...\ ,X_{i-1} &\lt x_{(i)} \\
X_{i} &= x_{(i)} \\
X_{i+1},\ ...\ ,X_{n} &\gt x_{(i)}
\end{aligned}\right.
$$
上記はすべて独立であることから
$$
\begin{aligned}
P( &X_{1},\ ...\ ,X_{i-1} \lt x_{(i)},\ X_{i} = x_{(i)},\ X_{i+1},\ ...\ ,X_{n} \gt x_{(i)}) \\
&= P( X_{1},\ ...\ ,X_{i-1} \lt x_{(i)}) \cdot
P(X_{i} = x_{(i)}) \cdot P(X_{i+1},\ ...\ ,X_{n} \gt x_{(i)})\\
&=F^{i-1}(x_{(i)}) \cdot f(x_{(i)}) \cdot (1-F(x_{(i)}))^{n-i} \\
&=f(x_{(i)})F^{i-1}(x_{(i)}) (1-F(x_{(i)}))^{n-i} \\
\end{aligned}
$$
$${X_{1},\ ...\ ,X_{n}}$$ の並べ方は $${\dfrac{n!}{(i-1)!(n-i)!}}$$ 通りあることから、順序統計量 $${X_{(i)}=x_{(i)}}$$ となる確率、すなわち、 $${X_{(i)}}$$ の確率密度関数 $${f_{(X_{(i)})}(x_{(i)})}$$ は
$$
\begin{aligned}
f_{X_{(i)}}(x_{(i)}) &=P(X_{(i)}=x_{(i)}) \\
&= \dfrac{n!}{(i-1)!(n-i)!} P( X_{1},\ ...\ ,X_{i-1} \lt x_{(i)},\ X_{i} = x_{(i)},\ X_{i+1},\ ...\ ,X_{n} \gt x_{(i)}) \\
&=\dfrac{n!}{(i-1)!(n-i)!}f(x_{(i)})F^{i-1}(x_{(i)}) (1-F(x_{(i)}))^{n-i} \\
&=\dfrac{1}{\Beta(i,n+1-i)}f(x_{(i)})F^{i-1}(x_{(i)}) (1-F(x_{(i)}))^{n-i} \\
\end{aligned}
$$
となります。
[2] X(i) の累積分布関数の従う確率分布
次に、累積分布関数の確率変数 $${Y_{i}=F(X_{(i)})}$$ の確率密度関数 $${f_{Y_{i}}(y)}$$ を導出します。
$${X_{(i)} \rightarrow Y_{i}}$$ の変数変換により求めます。
まず、確率密度関数を全領域で積分すると 1 となるため、以下が成り立ちます。
$$
\begin{aligned}
\int_{-\infty}^{\infty} f_{X_{(i)}}(x_{(i)}) dx_{(i)}=1
\end{aligned}
$$
ここで、置換積分を利用し、$${x_{(i)}}$$ を $${y=F(x_{(i)})}$$ に変換します。
$$
\left\{ \begin{aligned}
&y=F(x_{(i)}) \\
&dy = f(x_{(i)})dx_{(i)} \\
&x_{(i)}=F^{-1}(y) \\
&y:0 \rightarrow 1
\end{aligned}\right.
$$
左辺を変形すると、
$$
\begin{aligned}
\int_{-\infty}^{\infty} &f_{X_{(i)}}(x_{(i)}) dx_{(i)} \\
&=\int_{-\infty}^{\infty} \dfrac{1}{\Beta(i,n+1-i)}
f(x_{(i)})F^{i-1}(x_{(i)}) (1-F(x_{(i)}))^{n-i} dx_{(i)} \\
&=\int_{-\infty}^{\infty} \dfrac{1}{\Beta(i,n+1-i)}
\{F(F^{-1}(y)) \}^{i-1} (1-F(F^{-1}(y)))^{n-i} f(x_{(i)}) dx_{(i)} \\
&=\int_{0}^{1} \dfrac{1}{\Beta(i,n+1-i)}
y^{i-1} (1-y)^{n-i} dy \\
&=\int_{0}^{1} f_{Y_{i}}(y) dy =1\\
\end{aligned}
$$
よって、
$$
\begin{aligned}
f_{Y_{i}}(y)
&=\dfrac{y^{i-1} (1-y)^{n-i} }{\Beta(i,n+1-i)} \\
\end{aligned}
$$
が成り立ち、 $${Y_{i} \sim Beta(i,n+1-i)}$$ が導かれます。
[3] Yi の期待値、最頻値、中央値
次に、 $${Y_{i}}$$ の期待値、最頻値、中央値の導出をします。
中央値については解析的に解くことができないため、途中までの計算となります。
期待値
$${Y_{i} \sim Beta(i, n+1-i)}$$ の期待値 $${E[Y_{i}]}$$ は
$$
\begin{aligned}
E[Y_{i}]
&=\int_{0}^{1} y\dfrac{y^{i-1}(1-y)^{n-i}}
{\Beta(i,n+1-i)} dy \\
&=\int_{0}^{1}\dfrac{n!}{(i-1)!(n-i)!}
y^{i}(1-y)^{n-i} dy \\
&=\dfrac{i}{n+1}
\int_{0}^{1}\dfrac{(n+1)!}{i!(n+1-i)!}
y^{i}(1-y)^{n-i} dy \\
&=\dfrac{i}{n+1}
\int_{0}^{1}\dfrac{y^{i}(1-y)^{n-i}}
{\Beta(i+1,n+1-i)} dy \\
&=\dfrac{i}{n+1}
\end{aligned}
$$
中央値
$${Y_{i} \sim Beta(i, n+1-i)}$$ の中央値を計算する前に、$${Y_{i}}$$ の累積分布関数 $${F_{Y_{i}}(y)}$$ について考えます。
$$
\begin{aligned}
F_{Y_{i}}(y)
&=\int_{0}^{y}\dfrac{y^{i-1}(1-y)^{n-i}}{\Beta(i,n+1-i)} dy\\
&=\int_{0}^{y}\dfrac{n!}{(i-1)!(n-i)!} \cdot \dfrac{(y^{i})'}{i} \cdot (1-y)^{n-i} dy\\
&=\left[{}_{n}C_{i}y^{i} (1-y)^{n-i} \right]^{y}_{0}
-\int_{0}^{y} \dfrac{n!}{i!(n-i)!} (n-i)\cdot (-1)\cdot(1-y)^{n-i-1} dy\\
&={}_{n}C_{i}y^{i} (1-y)^{n-i}
+\int_{0}^{y} {}_{n}C_{i+1} (i+1)y^{i}(1-y)^{n-i-1} dy\\
&=\cdots \\
&=\sum_{k=i}^{n} {}_{n}C_{k}y^{k} (1-y)^{n-k} \\
&=1-\sum_{k=0}^{i-1} {}_{n}C_{k}y^{k} (1-y)^{n-k}
\end{aligned}
$$
以上より、二項分布 $${B(n,y)}$$ の上側確率と等しくなりますが、中央値は解析的に解くことができないため、近似式を利用します。
有名な近似式として Benard の近似式 (Benard's Approximation) があり、 以下の式で表されます。
$$
Y_{i} = F(X_{(i)}) \approx \dfrac{i-0.3}{n+0.4}
$$
近似式を用いたくない場合は、EXCEL や Google SHEETS では、 BETAINV 関数が用意されています。
Python では、ライブラリ Scipy の scipy.stats.beta.ppf を使用できます。
最頻値
$${Y_{i} \sim Beta(i, n+1-i)}$$ の最頻値は、確率密度関数 $${f_{Y_{i}}(y)}$$ を微分して求めると、
$$
\begin{aligned}
f'_{Y_{i}}(y)
&=\dfrac{d}{dy}\left(\dfrac{y^{i-1}(1-y)^{n-i}}{\Beta(i,n+1-i)} \right) \\
&= \dfrac{1}{\Beta(i,n+1-i)}\left\{
(i-1)y^{i-2}(1-y)^{n-i}-y^{i-1}(n-i)y^{n-i-1} \right\} \\
&= \dfrac{y^{i-2}y^{n-i-1}}{\Beta(i,n+1-i)}\left\{
(i-1)(1-y)-y(n-i) \right\} \\
&= \dfrac{y^{i-2}y^{n-i-1}}{\Beta(i,n+1-i)}\left\{
(i-1)-y(n-1) \right\} \\
\end{aligned}
$$
$${f'_{Y_{i}}(y) =0}$$ とすると、
$$
\begin{aligned}
y= \dfrac{i-1}{n-1}
\end{aligned}
$$
となり、$${Y_{i}}$$ の最頻値は $${\dfrac{i-1}{n-1}}$$ が導かれます。
[4] 簡易シミュレーションによる各方式の推定精度の比較
前置き
本項では、3 通りの方式に加え、中央値について真の値を使用した場合の、計 4 通りについて、pythonを使用したシミュレーションにより未知パラメータの推定の精度を比較します。
今回は、ワイブル分布に従う乱数より得られた観測値から、確率紙による推定を用いて計算した形状パラメータ $${m}$$、尺度パラメータ $${\eta}$$ の推定値により比較します。
確率紙による推定に関する詳細は以下の記事の [2] をご覧ください
・シミュレーションは以下の手順で実施します。
ワイブル分布に従う乱数を生成する
得られた乱数(観測値)より確率紙による推定方法に基づいて $${m,\eta}$$ の推定値を計算する。なお、累積分布関数の値には以下の4通りの計算式を使用
平均ランク
メジアンランク (scipy.stats.beta.ppf を使用)
Benardの近似式
モードランク
上記の試行を10000回繰り返し、計算した推定値の平均と不偏分散により、結果を判定する。
各方式の推定精度の評価には計算した推定値の平均値と真値の相対誤差と分散を真値の二乗で割った、相対化した分散を使用します。
未知パラメータの真値を $${\theta}$$、$${i}$$ 回目の推定値を $${\hat{\theta}_{i}}$$、推定値の平均を $${\hat{\theta}_{mean}}$$、不偏分散を $${S^{2}_{\hat{\theta}}}$$、試行回数を $${N}$$ として
推定値の相対誤差 $${=\dfrac{\hat{\theta}_{mean}-\theta}{\theta}}$$
相対化した分散 $${=\dfrac{S^{2}_{\hat{\theta}}}{\theta^{2}}}$$
と表せます。
推定値の平均 $${\hat{\theta}_{mean}}$$、不偏分散 $${S^{2}_{\hat{\theta}}}$$ については
$$
\begin{aligned}
\hat{\theta}_{mean} = \dfrac{1}{N}\sum_{i=1}^{N} \hat{\theta}_{i} ,\
S^{2}_{\hat{\theta}} = \dfrac{1}{N-1}\sum_{i=1}^{N} (\hat{\theta}_{i} - \hat{\theta}_{mean})^{2}
\end{aligned}
$$
とします。
結果
最初に、$${m}$$ を $${0.1}$$ から $${5}$$ まで変化させたときの推定値の平均の相対誤差、相対化した分散をグラフ化したものを以下に示します。
条件:$${m=0.1,\ ...\ ,5.0}$$ 、$${\eta=100}$$ 、乱数の数 $${n=10}$$ 、試行回数 $${N=10000}$$

$${m}$$ が小さい場合は $${\eta}$$ の推定値は非常に大きくなります。$${m =0.1,\ ...\ ,0.5}$$ の場合は別途以下のグラフに示します。
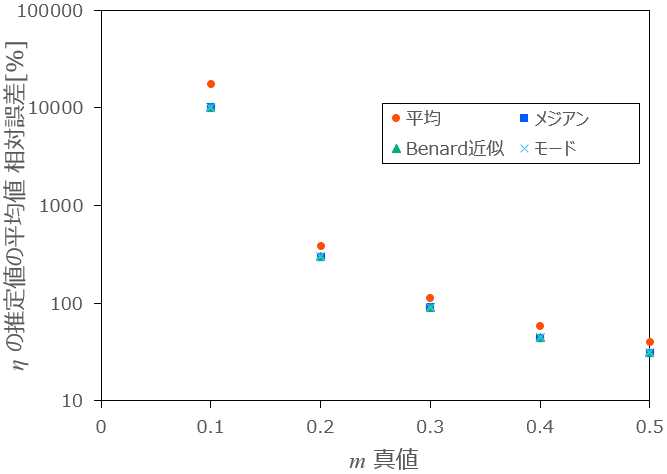
次に、$${\eta}$$ を $${1}$$ から $${10000}$$ まで変化させたときの推定値の平均の相対誤差、相対化した分散をグラフ化したものを以下に示します。
条件:$${m=0.5}$$ 、$${\eta=1,2,5,10,\ ...\ ,10000}$$ 、乱数の数 $${n=10}$$ 、試行回数 $${N=10000}$$

最後に、乱数の数 $${n}$$ を $${5}$$ から $${10000}$$ まで変化させたときの推定値の平均値の相対誤差、相対化した分散をグラフ化したものを以下に示します。
条件:$${m=0.5}$$ 、$${\eta=100}$$ 、乱数の数 $${n=5,10,20,50,\ ...\ ,10000}$$ 、試行回数 $${N=10000}$$

まとめ
以上の結果から、形状パラメータ $${m}$$ について推定に最も適しているのは、メジアンランクで真の値を用いた場合です。
次いで、Benardの近似式の場合ですが、両者にはほとんど違いがありません。(Benardの近似式と中央値の真値との誤差は小さい)
3番目は平均ランクです。分散は最も小さいですが、これはもともと相対誤差が 12% 程度小さいためであり、メジアンランクの場合の分散と比較して、実質的には差はほとんどありません。
最も適さないのはモードランクであり、相対誤差と分散が4つの中で最も大きい結果となります。
形状パラメータ $${\eta}$$ については、推定に最も適しているのは、モードランクを用いた場合です。
次点で、メジアンランクの真値を使用した場合で、分散がモードランクよりも若干大きくなっています。
3番目はBenardの近似式の場合ですが、メジアンランクの真の値を使用した場合と、ほとんど違いがありません。
最も適さないのは平均ランクで、最も相対誤差と分散が大きい結果となります。
以上、モードランクについては $${m}$$ の推定に誤差が大きすぎることを考えれば、総合的にはメジアンランクを使用した場合が推定としては最も適しています。Benard近似を用いた場合でも大きな違いはありません。
[5] Python ソースコード
以下、簡易シミュレーションで使用したPythonのソースコードです。
numpy,pandas,scipy は標準ライブラリにありませんので、インストールが必要になります。
バージョン情報
python : 3.12.0
numpy : 1.26.2
pandas : 2.1.3
scipy : 1.13.0
import numpy as np
import pandas as pd
import scipy
# 最小二乗法の計算
def LSM(x,y):
x_bar = np.average(x)
y_bar = np.average(y)
a = (np.dot(x-x_bar,y-y_bar) / np.sum((x-x_bar) ** 2))
b = y_bar - x_bar * a
return a,b
# num個の乱数によるパラメータの推定を num_of_times 回実施した計算結果を出力する
def CALC(m,eta,num,num_of_times):
# 計算結果の配列の定義
m_hat_mean_arr = np.empty(0) #平均値ランク m
eta_hat_mean_arr= np.empty(0) #平均値ランク η
m_hat_med_arr = np.empty(0) #メジアンランク m
eta_hat_med_arr = np.empty(0) #メジアンランク η
m_hat_ber_arr = np.empty(0) #Benardの近似式 m
eta_hat_ber_arr = np.empty(0) #Benardの近似式 η
m_hat_mod_arr = np.empty(0) #モードランク m
eta_hat_mod_arr = np.empty(0) #モードランク η
# 累積分布関数F(x)の生成 #累積分布関数は乱数に依存しないため、ループの外で実施し、計算量を減らす
F = np.arange(1,num+1)
F_mean = F/(num+1) #平均値ランク
F_med = scipy.stats.beta.ppf(0.5, F, num+1-F) #メジアンランク
F_ber = (F-0.3)/(num +0.4) #Benardの近似式
F_mod = (F-1)/(num - 1) #モードランク
# y = ln {-ln(1-F(x)) }の計算
y_mean = np.log(-np.log(1-F_mean))
y_med = np.log(-np.log(1-F_med))
y_ber = np.log(-np.log(1-F_ber))
y_mod = np.log(-np.log(1-F_mod[1:-1])) #モードランクでは 最初と最後のデータは発散するため除外
# num 個の乱数によるパラメータの推定を num_of_times 回実施
for i in range(num_of_times):
# 乱数生成用
rng = np.random.default_rng()
# U(0,1)の一様乱数を生成
u = rng.random(num)
# 昇順に並び替え
u = np.sort(u)
# 逆関数法によりワイブル分布に従う乱数の生成
x = eta * (-np.log(1-u)) **(1/m)
logx = np.log(x)
logx_bar = np.average(logx)
# 最小二乗法により、傾きa, 切片b を計算
a_mean,b_mean = LSM(logx,y_mean)
a_med,b_med = LSM(logx,y_med)
a_ber,b_ber = LSM(logx,y_ber)
a_mod,b_mod = LSM(logx[1:-1],y_mod)
#a,bから m,η を計算
m_hat_mean,eta_hat_mean = a_mean, np.exp(-b_mean/a_mean)
m_hat_med,eta_hat_med = a_med, np.exp(-b_med/a_med)
m_hat_ber,eta_hat_ber = a_ber, np.exp(-b_ber/a_ber)
m_hat_mod,eta_hat_mod = a_mod, np.exp(-b_mod/a_mod)
# 各方式の計算結果を配列に追加
m_hat_mean_arr = np.append(m_hat_mean_arr, m_hat_mean)
m_hat_med_arr = np.append(m_hat_med_arr, m_hat_med)
m_hat_ber_arr = np.append(m_hat_ber_arr, m_hat_ber)
m_hat_mod_arr = np.append(m_hat_mod_arr, m_hat_mod)
eta_hat_mean_arr = np.append(eta_hat_mean_arr, eta_hat_mean)
eta_hat_med_arr = np.append(eta_hat_med_arr, eta_hat_med)
eta_hat_ber_arr = np.append(eta_hat_ber_arr, eta_hat_ber)
eta_hat_mod_arr = np.append(eta_hat_mod_arr, eta_hat_mod)
# 平均、不偏分散を計算
m_hat_mean_avg = np.average(m_hat_mean_arr)
m_hat_mean_var = np.var(m_hat_mean_arr,ddof=1)
m_hat_med_avg = np.average(m_hat_med_arr)
m_hat_med_var = np.var(m_hat_med_arr,ddof=1)
m_hat_ber_avg = np.average(m_hat_ber_arr)
m_hat_ber_var = np.var(m_hat_ber_arr,ddof=1)
m_hat_mod_avg = np.average(m_hat_mod_arr)
m_hat_mod_var = np.var(m_hat_mod_arr,ddof=1)
eta_hat_mean_avg = np.average(eta_hat_mean_arr)
eta_hat_mean_var = np.var(eta_hat_mean_arr,ddof=1)
eta_hat_med_avg = np.average(eta_hat_med_arr)
eta_hat_med_var = np.var(eta_hat_med_arr,ddof=1)
eta_hat_ber_avg = np.average(eta_hat_ber_arr)
eta_hat_ber_var = np.var(eta_hat_ber_arr,ddof=1)
eta_hat_mod_avg = np.average(eta_hat_mod_arr)
eta_hat_mod_var = np.var(eta_hat_mod_arr,ddof=1)
#結果出力用配列の作成
outdata = np.array([m, eta, num, num_of_times,
m_hat_mean_avg, m_hat_mean_var, m_hat_med_avg, m_hat_med_var,
m_hat_ber_avg, m_hat_ber_var, m_hat_mod_avg, m_hat_mod_var,
eta_hat_mean_avg, eta_hat_mean_var, eta_hat_med_avg, eta_hat_med_var,
eta_hat_ber_avg, eta_hat_ber_var, eta_hat_mod_avg, eta_hat_mod_var
])
#結果の二次元配列化 (列を結合できるように)
outdata = outdata.reshape(len(outdata),1)
#結果表示
print(f'平均値ランクによるmの推定値の平均、分散 :{m_hat_mean_avg}、{m_hat_mean_var}')
print(f'メジアンランクによるmの推定値の平均、分散:{m_hat_med_avg}、{m_hat_med_var}')
print(f'Benard近似によるmの推定値の平均、分散 :{m_hat_ber_avg}、{m_hat_ber_var}')
print(f'モードランクによるmの推定値の平均、分散 :{m_hat_mod_avg}、{m_hat_mod_var}')
print(f'平均値ランクによるηの推定値の平均、分散 :{eta_hat_mean_avg}、{eta_hat_mean_var}')
print(f'メジアンランクによるηの推定値の平均、分散:{eta_hat_med_avg}、{eta_hat_med_var}')
print(f'Benard近似によるηの推定値の平均、分散 :{eta_hat_ber_avg}、{eta_hat_ber_var}')
print(f'モードランクによるηの推定値の平均、分散 :{eta_hat_mod_avg}、{eta_hat_mod_var}')
return outdata
def main():
#出力結果格納用配列
dataset = np.empty((20,0))
# パラメータの設定
m = 0.5 #形状パラメータ
eta = 100 #尺度パラメータ
num = 10 #生成乱数の個数
num_of_times = 10000 #試行回数
No = 1
#for m in np.arange(0.1,5.01,0.1):
#for eta in np.array((1,2,5,10,20,50,100,200,500,1000,2000,5000,10000)):
for num in np.array((5,10,20,50,100,200,500,1000,2000,5000,10000)):
#計算条件の表示
print(f'No.{No}: m={m}, η={eta}, 乱数の数={num}, 試行回数={num_of_times}の条件で計算中')
#各パラメータの計算結果の列を結合
dataset = np.append(dataset,CALC(m,eta,num,num_of_times),axis=1)
No += 1
# ファイル出力
## 表題作成
index1 = ['mの真値', 'ηの真値', '生成乱数の個数', '試行回数',
'平均値ランク:mの推定値の平均', '平均値ランク:mの推定値の分散', 'メジアンランク:mの推定値の平均', 'メジアンランク:mの推定値の分散',
'Benard近似:mの推定値の平均', 'Benard近似:mの推定値の分散', 'モードランク:mの推定値平均', 'モードランク:mの推定値の分散',
'平均値ランク:ηの推定値の平均', '平均値ランク:ηの推定値の分散', 'メジアンランク:ηの推定値の平均', 'メジアンランク:ηの推定値の分散',
'Benard近似:ηの推定値の平均', 'Benard近似:ηの推定値の分散', 'モードランク:ηの推定値の平均', 'モードランク:ηの推定値の分散',
]
header1 = []
for i in range(dataset.shape[1]):
header1.append(f'No.{i+1}')
pd_out = pd.DataFrame(dataset,columns=header1, index=index1)
# csvデータ出力 #shift-jis でないとエクセルで文字化け
outname = f'm={m}_η={eta}_乱数の数={num}_試行回数={num_of_times}.csv'
pd.DataFrame(pd_out).to_csv(outname, encoding='shift-jis')
input('計算が完了しました。ENTERで最初からやり直します。')
if __name__ == "__main__":
while(1):
main()
