【ワイブル分布】形状パラメータの最尤推定量の補正係数に関する補足

はじめに

今回はワイブル分布の形状パラメータ $${m}$$ の最尤推定量 $${\hat{m}}$$ を不偏推定量(期待値がパラメータの真値と等しい推定量)とする補正係数について解説します。この補正係数により、ワイブル分布の未知パラメータ推定において、確率紙による方法よりも推定のばらつきを小さくすることができます。
補正係数については、 $${n}$$ 個の試験において、観測値がすべて得られた場合、未知パラメータに依存せず、観測値の数 $${n}$$ のみに依存します。 $${r}$$ 個の観測値が得られた段階で打ち切る場合も、未知パラメータに依存せず、$${r,n}$$ のみに依存します。
ワイブル分布の最尤推定量に関する詳細については上の記事、
補正係数を用いた最尤推定量の改良方法については下の記事
をご覧ください。

概要

前置き

以下のように確率変数を定義します。

• 確率変数 $${X_{1},\ ...\ ,X_{n}}$$ は互いに独立に形状パラメータ $${m}$$ 、尺度パラメータ $${\eta}$$ のワイブル分布 $${W(m,\eta)}$$ に従い、その確率密度関数を $${f(x)}$$、累積分布関数を $${F(x)}$$ とする

• $${X_{(1)},\ ...\ ,X_{(n)}}$$ を $${X_{1},\ ...\ ,X_{n}}$$ の順序統計量とする
  $${\big(X_{(i)}}$$ は $${X_{1},\ ...\ ,X_{n}}$$ の中で $${i}$$ 番目に小さい確率変数$${\big)}$$

• $${X_{i}}$$ から得られる観測値を $${x_{i}}$$ 、$${X_{(i)}}$$ から得られる観測値を $${x_{(i)}}$$ とする$${(i=1,\ ...\ ,n)}$$

また、確率密度関数 $${f(x)}$$ 、累積分布関数 $${F(x)}$$ は

$$
\begin{aligned}
f(x)&=\dfrac{m}{\eta}\left(\dfrac{x}{\eta} \right)^{m-1}
\exp\left\{-\left(\dfrac{x}{\eta} \right)^{m} \right\} \\
F(x)&=1-\exp\left\{-\left(\dfrac{x}{\eta} \right)^{m} \right\} \\
\end{aligned}
$$

と表されます。

最尤推定量を $${\hat{m}}$$ 、不偏推定量とする補正係数を $${C_{m}}$$ とすると、以下の式が成り立ちます。

$$
\begin{aligned}
E[C_{m}\hat{m}] = C_{m}E[\hat{m}] = m
\end{aligned}
$$

よって、補正係数 $${C_{m}}$$ は

$$
\begin{aligned}
C_{m} =\dfrac{1}{\dfrac{E\left[ \hat{m} \right]}{m}} =\dfrac{1}{E\left[ \dfrac{\hat{m}}{m} \right]}
\end{aligned}
$$

と表されます。

[1] 【概要】すべての観測値が得られた場合の形状パラメータの補正係数

$${n}$$ 個の部品の寿命試験において、$${n}$$ 個すべての観測値が得られた場合の補正係数について概説します。

補正係数は未知パラメータ $${m,\eta}$$ に依存せず、 $${n}$$ のみに依存します。
まず、形状パラメータの最尤推定量を真値で割った $${\dfrac{\hat{m}}{m}=k_{n}}$$ は、母数 1 の指数分布 $${Exp(1)}$$ から独立に得られた観測値を $${z_{1},\ ...\ ,z_{n}}$$ とすると、以下の式を満たします。

$$
\begin{aligned}
\dfrac{1}{k_{n}}
+\dfrac{1}{n}\sum_{i=1}^{n}\ln{z_{i}}
- \dfrac{ \sum_{i=1}^{n} z_{i}^{k_{n}} \ln z_{i} }
{ \sum_{i=1}^{n} z_{i}^{k_{n}}}
&=0
\end{aligned}
$$

また、補正係数 $${C_{m}}$$ については $${k_{n} \left( =\dfrac{\hat{m}}{m} \right)}$$ を用いて、

$$
\begin{aligned}
C_{m} =\dfrac{1}{E\left[ \dfrac{\hat{m}}{m} \right]} = \dfrac{1}{E[k_{n}]}
\end{aligned}
$$

と表されます。

次に、$${k_{n}}$$ の期待値 $${E[k_{n}]}$$ を乱数を用いた解析（モンテカルロ法）により計算し、縦軸に $${\dfrac{1}{E[k_{n}]-1}}$$ 、横軸に $${n}$$ をとると、綺麗な直線となります。これを利用して、補正係数は以下のように表すことができます。

$$
\begin{aligned}
C_{m} &= \dfrac{an+b}{an+b+1} \\
(a = 0.72593681 &,\ b = -1.365817779 )
\end{aligned}
$$

詳細は "[1] 【詳細】すべての観測値が得られた場合の形状パラメータの補正係数" をご覧ください。

[2] 【概要】打ち切りありの場合の形状パラメータの補正係数

$${n}$$ 個の部品の寿命試験において、 $${r}$$ 個の観測値が得られた段階で試験を打ち切る場合の補正係数について概説します。
残りの $${n-r}$$ 個については観測値は得られませんが、小さい順に $${r}$$ 番目の観測値より大きいという条件があります。

この場合の補正係数は未知パラメータ $${m,\eta}$$ に依存せず、$${r,n}$$ のみに依存します。
まず、形状パラメータの最尤推定量を真値で割った $${\dfrac{\hat{m}}{m}=k_{r,n}}$$ は、母数 1 の指数分布 $${Exp(1)}$$ から独立に得られた観測値のうち、小さい順に $${r}$$ 個並べたものを $${z_{(1)},\ ...\ ,z_{(r)}}$$ とすると、以下の式を満たします。

$$
\begin{aligned}
\dfrac{1}{k_{r,n}} + \dfrac{1}{r}\sum_{i=1}^{r}\ln z_{(i)}
-\dfrac{ \sum_{i=1}^{r} z_{(i)} ^{k_{r,n}} \ln z_{(i)}
+ (n-r) z_{(r)}^{k_{r,n}} \ln z_{(r)} }
{ \sum_{i=1}^{r} z_{(i)} ^{k_{r,n}}
+(n-r) z_{(r)} ^{k_{r,n}} }
&=0
\end{aligned}
$$

また、補正係数 $${C_{m}}$$ については $${k_{r,n} \left( =\dfrac{\hat{m}}{m} \right)}$$ の期待値 $${E[k_{r,n}]}$$ を用いて、

$$
\begin{aligned}
C_{m} =\dfrac{1}{E\left[ \dfrac{\hat{m}}{m} \right]} =\dfrac{1}{E[k_{r,n}]}
\end{aligned}
$$

と表されます。

次に、$${r}$$ を一定値として、$${E[k_{r,n}]}$$ を乱数を用いた解析により計算し、縦軸に $${\dfrac{1}{\dfrac{r}{r-2}-E[k_{r,n}]}}$$ 、横軸に $${n}$$ をとると、ほぼ直線となります。 [1] の場合と比較して、計算結果の値のばらつきが大きく、線形近似により正確な値を算出するのが困難です。良い方法が見つかり次第更新します。

詳細は "[2] 【詳細】打ち切りありの場合の形状パラメータの補正係数" をご覧ください。

[1] 【詳細】すべての観測値が得られた場合の形状パラメータの補正係数

方針

補正係数を $${C_{m}}$$ として、$${E[C_{m}\hat{m}]=m}$$ より

$$
\begin{aligned}
C_{m} =\dfrac{1}{\dfrac{E\left[ \hat{m} \right]}{m}} =\dfrac{1}{E\left[ \dfrac{\hat{m}}{m} \right]}
\end{aligned}
$$

となることから、以下の手順で算出します。

1. $${\dfrac{\hat{m}}{m}=k_{n}}$$ を求める関係式の導出

2. 乱数を用いた解析による期待値 $${E[k_{n}]}$$ と補正係数の計算

[1]-1 形状パラメータ m の最尤推定量 ÷ 真値を求める関係式の導出

$${n}$$ 個の部品の寿命試験において、$${n}$$ 個すべての観測値 $${x_{1},\ ...\ ,x_{n}}$$ が得られた場合の補正係数について詳説します。

まず、$${m}$$ の最尤推定量 $${\hat{m}}$$ は以下の式 $${(1.1)}$$ を満たします。

$$
\begin{aligned}
g_{X_{1},\ ...\ ,X_{n}}&(\hat{m})\\
&= \dfrac{1}{\hat{m}} + \dfrac{1}{n}\sum_{i=1}^{n}\ln{x_{i}}
-\dfrac{\sum_{i=1}^{n} x_{i}^{\hat{m}} \ln{x_{i}}}{\sum_{i=1}^{n} x_{i}^{\hat{m}}} =0 \hspace{25pt} (1.1)
\end{aligned}
$$

ここで $${Z_{i} = \left( \dfrac{X_{i}}{\eta} \right)^{m}}$$ として、$${X_{i} \rightarrow Z_{i}}$$ の変数変換により、$${(1.1)}$$ 式の $${x_{i}}$$ を $${z_{i}}$$ で表します。
このとき、$${Z_{i}}$$ の従う分布は母数 $${1}$$ の指数分布 $${=Exp(1)}$$ となります。
$${x_{i}=\eta z_{i}^{\frac{1}{m}}}$$ より、$${(1.1)}$$ 式を変形すると、

$$
\begin{aligned}
g_{Z_{1},\ ...\ ,Z_{n}}(\hat{m})
&= \dfrac{1}{\hat{m}} + \dfrac{1}{n}\sum_{i=1}^{n}\ln{\eta z_{i}^{\frac{1}{m}}}
-\dfrac{\sum_{i=1}^{n} \left( \eta z_{i}^{\frac{1}{m}} \right)^{\hat{m}} \ln \eta z_{i}^{\frac{1}{m}}}
{\sum_{i=1}^{n} \left( \eta z_{i}^{\frac{1}{m}} \right)^{\hat{m}}} \\
&= \dfrac{1}{\hat{m}} + \dfrac{1}{n}\left( \dfrac{1}{m}\sum_{i=1}^{n}\ln{z_{i}} +\sum_{i=1}^{n} \ln \eta \right)
-\dfrac{\eta^{\hat{m}} \sum_{i=1}^{n} z_{i}^{\frac{\hat{m}}{m}} \left( \dfrac{1}{m}\ln z_{i} + \ln \eta \right)}
{\eta^{\hat{m}}\sum_{i=1}^{n} z_{i}^{\frac{\hat{m}}{m}}} \\
&= \dfrac{1}{\hat{m}} + \dfrac{1}{mn}\sum_{i=1}^{n}\ln{z_{i}} +\ln \eta
-\dfrac{1}{m}\dfrac{ \sum_{i=1}^{n} z_{i}^{\frac{\hat{m}}{m}} \ln z_{i} }
{\sum_{i=1}^{n} z_{i}^{\frac{\hat{m}}{m}}}-\ln \eta \\
&= \dfrac{1}{m} \left( \dfrac{m}{\hat{m}}
+\dfrac{1}{n}\sum_{i=1}^{n}\ln{z_{i}}
- \dfrac{ \sum_{i=1}^{n} z_{i}^{\frac{\hat{m}}{m}} \ln z_{i} }
{ \sum_{i=1}^{n} z_{i}^{\frac{\hat{m}}{m}}} \right) \\
\end{aligned}
$$

ここで $${\dfrac{\hat{m}}{m} = k_{n}}$$ とすると、

$$
\begin{aligned}
g_{Z_{1},\ ...\ ,Z_{n}}(k_{n})
&= \dfrac{1}{m} \left( \dfrac{1}{k_{n}}
+\dfrac{1}{n}\sum_{i=1}^{n}\ln{z_{i}}
- \dfrac{ \sum_{i=1}^{n} z_{i}^{k_{n}} \ln z_{i} }
{ \sum_{i=1}^{n} z_{i}^{k_{n}}} \right) \\
&=0
\end{aligned}
$$

となります。以上より、$${k_{n}}$$ については以下の式 $${(1.2)}$$ を満たします。

$$
\begin{aligned}
\dfrac{1}{k_{n}}
+\dfrac{1}{n}\sum_{i=1}^{n}\ln{z_{i}}
- \dfrac{ \sum_{i=1}^{n} z_{i}^{k_{n}} \ln z_{i} }
{ \sum_{i=1}^{n} z_{i}^{k_{n}}}
&=0　\hspace{25pt} (1.2)
\end{aligned}
$$

$${z_{i}}$$ は母数が 1 の指数分布 $${Exp(1)}$$ から得られる観測値であることから、$${k_{n}}$$ は $${m,\eta}$$ に依存しないことが分かります。よって、$${k_{n}}$$ の期待値 $${E[k_{n}]}$$ は未知パラメータ $${m,\eta}$$ に依存せず、 $${n}$$ のみに依存する関数となります。

[1]-2 [m の最尤推定量 ÷ 真値] の期待値、補正係数の計算

次に、$${k_{n}}$$ の期待値 $${E[k_{n}]}$$ については解析的には解くことができないため、以下の手順で乱数を用いた解析（モンテカルロ法）により計算します。

• 母数 1 の指数分布に従う乱数を生成

• 得られた乱数（観測値）から、$${(1.2)}$$ 式により $${k_{n}}$$ を算出

• 上記の試行を 1000 万回繰り返し、算出した $${k_{n}}$$ の平均をとり、期待値とする

また、$${E[k_{n}]=E\left[ \dfrac{\hat{m}}{m} \right]}$$ については $${n}$$ のみの関数となり、 $${n \rightarrow \infty}$$ で $${E[k_{n}] \rightarrow 1}$$ となることから、期待値 $${E[k_{n}]}$$ を以下のように仮定します。

$$
\begin{aligned}
E[k_{n}]=\dfrac{1}{an+b}+1
\end{aligned}
$$

この場合、$${\dfrac{1}{E[k_{n}]-1}}$$ は $${n}$$ について直線となります。実際に、縦軸に $${\dfrac{1}{E[k_{n}]-1}}$$ 、横軸に生成乱数の数 $${n}$$ をとったグラフは以下のように綺麗な直線となります。

条件：生成乱数の数 $${n=4,\ ...\ ,50}$$ 、試行回数 $${N=10,000,000}$$

図１： n と E[k_{n}]-1 の逆数の関係

上記の計算結果を利用して、最小二乗法により $${\dfrac{1}{E[k_{n}]-1}}$$ を $${n}$$ の一次式で表すと、

$$
\begin{aligned}
\dfrac{1}{E[k_{n}]-1} = 0.72593681n - 1.365817779
\end{aligned}
$$

となります。

以上より、補正係数は以下のようになります。

$$
\begin{aligned}
C_{m} &= \dfrac{an+b}{an+b+1} \\
(a = 0.72593681,&\ b = -1.365817779 )
\end{aligned}
$$

[2] 【詳細】打ち切りありの場合の形状パラメータの補正係数

方針

[1] と同様に以下の手順で補正係数を計算します。

1. $${\dfrac{\hat{m}}{m}=k_{r,n}}$$ を求める関係式の導出

2. 乱数を用いた解析による期待値 $${E[k_{r,n}]}$$ と補正係数の計算

[2]-1 形状パラメータ m の最尤推定量 ÷ 真値を求める関係式の導出

$${n}$$ 個の部品の寿命試験において、小さい順に $${r}$$ 個の観測値 $${x_{(1)},\ ...\ ,x_{(r)}}$$ が得られた段階で試験を打ち切る場合の補正係数について詳説します。試験を打ち切ったため、$${x_{(r+1)},\ ...\ ,x_{(n)}}$$ については観測値が得られなかったとします。

観測値については、順序統計量のため、添え字が括弧つきの $${x_{(i)}}$$ を使用します。

この場合の $${m}$$ の最尤推定量 $${\hat{m}}$$ は以下の式 $${(2.1)}$$ を満たします。

$$
\begin{aligned}
g_{X_{(1)},\ …\ ,X_{(r)}}&(\hat{m}) \\
&= \dfrac{1}{\hat{m}} + \dfrac{1}{r}\sum_{i=1}^{r}\ln{x_{(i)}}
-\dfrac{\sum_{i=1}^{r} x_{(i)}^{\hat{m}} \ln{x_{(i)}}
+(n-r) x_{(r)}^{\hat{m}}\ln x_{(r)}}
{\sum_{i=1}^{r} x_{(i)}^{\hat{m}}
+(n-r) x_{(r)}^{\hat{m}} } \\
&=0 \hspace{25pt} (2.1)
\end{aligned}
$$

ここで、[1] の場合と同様に、$${Z_{(i)}=\left( \dfrac{X_{(i)}}{\eta} \right)^{m}}$$ として、 $${X_{(i)} \rightarrow Z_{(i)} (i=1,\ ...\ ,r)}$$ の変数変換により、$${(2.1)}$$ 式の $${x_{(i)}}$$ を $${z_{(i)}}$$ で表します。
このとき、$${Z_{(i)}}$$ は母数 $${1}$$ の指数分布 $${=Exp(1)}$$ の順序統計量となります。
$${x_{(i)}= \eta z_{(i)}^{\frac{1}{m}}}$$ より、 $${(2.1)}$$ 式を変形すると、

$$
\begin{aligned}
g_{Z_{(1)},\ ...\ ,Z_{(r)}}(\hat{m})
&= \dfrac{1}{\hat{m}} + \dfrac{1}{r}\sum_{i=1}^{r}\ln{\eta z_{(i)}^{\frac{1}{m}}}
-\dfrac{\sum_{i=1}^{r} \left( \eta z_{(i)}^{\frac{1}{m}} \right)^{\hat{m}} \ln{ \eta z_{(i)}^{\frac{1}{m}}}
+(n-r) \left( \eta z_{(r)}^{\frac{1}{m}} \right)^{\hat{m}} \ln \eta z_{(r)}^{\frac{1}{m}} }
{\sum_{i=1}^{r} \left( \eta z_{(i)}^{\frac{1}{m}} \right)^{\hat{m}}
+(n-r) \left( \eta z_{(r)}^{\frac{1}{m}} \right)^{\hat{m}} } \\
&= \dfrac{1}{\hat{m}}
+\dfrac{1}{r}\left( \dfrac{1}{m}\sum_{i=1}^{r}\ln{z_{(i)}} + \sum_{i=1}^{r} \ln \eta \right)
-\dfrac{\eta^{\hat{m}} \sum_{i=1}^{r} z_{(i)}^{\frac{\hat{m}}{m}}
\left( \dfrac{1}{m}\ln z_{(i)} + \ln \eta \right)
+(n-r) \eta^{\hat{m}} z_{(r)}^{\frac{\hat{m}}{m}} \left( \ln \eta + \dfrac{1}{m} \ln z_{(r)} \right) }
{\eta^{\hat{m}} \sum_{i=1}^{r} z_{(i)}^{\frac{\hat{m}}{m}}
+ (n-r) \eta^{\hat{m}} z_{(r)}^{\frac{\hat{m}}{m}} } \\
&= \dfrac{1}{\hat{m}}
+\dfrac{1}{mr} \sum_{i=1}^{r}\ln{z_{(i)}} + \ln \eta
-\dfrac{1}{m}\dfrac{\sum_{i=1}^{r} z_{(i)}^{\frac{\hat{m}}{m}} \ln z_{(i)}
+(n-r) z_{(r)}^{\frac{\hat{m}}{m}} \ln z_{(r)} }
{\sum_{i=1}^{r} z_{(i)}^{\frac{\hat{m}}{m}}
+ (n-r) z_{(r)}^{\frac{\hat{m}}{m}} }
-\dfrac{\sum_{i=1}^{r} z_{(i)}^{\frac{\hat{m}}{m}}
+(n-r) z_{(r)}^{\frac{\hat{m}}{m}} }
{\sum_{i=1}^{r} z_{(i)}^{\frac{\hat{m}}{m}}
+ (n-r) z_{(r)}^{\frac{\hat{m}}{m}} } \ln \eta \\
&= \dfrac{1}{m} \left( \dfrac{m}{\hat{m}}
+\dfrac{1}{r} \sum_{i=1}^{r}\ln{z_{(i)}}
-\dfrac{\sum_{i=1}^{r} z_{(i)}^{\frac{\hat{m}}{m}} \ln z_{(i)}
+(n-r) z_{(r)}^{\frac{\hat{m}}{m}} \ln z_{(r)} }
{\sum_{i=1}^{r} z_{(i)}^{\frac{\hat{m}}{m}}
+ (n-r) z_{(r)}^{\frac{\hat{m}}{m}} }
\right) \\
&=0
\end{aligned}
$$

ここで $${\dfrac{\hat{m}}{m} = k_{r,n}}$$ とすると、

$$
\begin{aligned}
g_{Z_{(1)},\ ...\ ,Z_{(r)}}(k_{r,n})
&= \dfrac{1}{m}\left( \dfrac{1}{k_{r,n}} + \dfrac{1}{r}\sum_{i=1}^{r}\ln z_{(i)}
-\dfrac{ \sum_{i=1}^{r} z_{(i)} ^{k_{r,n}} \ln z_{(i)}
+ (n-r) z_{(r)}^{k_{r,n}} \ln z_{(r)} }
{ \sum_{i=1}^{r} z_{(i)} ^{k_{r,n}}
+(n-r) z_{(r)} ^{k_{r,n}} }
\right) \\
&=0
\end{aligned}
$$

よって、 $${k_{r,n}=\dfrac{\hat{m}}{m}}$$ は 、以下の式 $${(2.2)}$$ を満たします。

$$
\begin{aligned}
\dfrac{1}{k_{r,n}} + \dfrac{1}{r}\sum_{i=1}^{r}\ln z_{(i)}
-\dfrac{ \sum_{i=1}^{r} z_{(i)} ^{k_{r,n}} \ln z_{(i)}
+ (n-r) z_{(r)}^{k_{r,n}} \ln z_{(r)} }
{ \sum_{i=1}^{r} z_{(i)} ^{k_{r,n}}
+(n-r) z_{(r)} ^{k_{r,n}} }
&=0 \hspace{25pt} (2.2)
\end{aligned}
$$

$${z_{(i)}}$$ は母数が 1 の指数分布 $${Exp(1)}$$ の順序統計量から得られる観測値であることから、$${k_{r,n}}$$ は $${m,\eta}$$ に依存しないことが分かります。よって、$${k_{r,n}}$$ の期待値 $${E[k_{r,n}]}$$ は未知パラメータ $${m,\eta}$$ に依存せず、 $${r}$$ と $${n}$$ に依存する関数となります。

[2]-2 [m の最尤推定量 ÷ 真値] の期待値、補正係数の計算

次に、$${k_{r,n}}$$ の期待値 $${E[k_{r,n}]}$$ については [1] と同様に、以下の手順で乱数を用いた解析により算出します。

• 母数 1 の指数分布に従う乱数を生成

• 得られた乱数（観測値）を昇順に並べ、小さい順に $${r}$$ 番目までの観測値のみを抽出

• $${(2.2)}$$ 式により $${k_{r,n}}$$ を算出

• 上記の試行を 1000 万回繰り返し、算出した $${k_{r,n}}$$ の平均をとり、期待値とする

また、$${r}$$ を一定として $${n \rightarrow \infty}$$ とした場合 $${E[k_{r,n}] \rightarrow \dfrac{r}{r-2}}$$ となります。導出過程が長いので、詳細は以下の記事をご覧ください

[1] の場合と同様に、縦軸に $${\dfrac{1}{\dfrac{r}{r-2}-E[k_{r,n}]}}$$ 、横軸に $${n}$$ をとったグラフは以下のようにほぼ直線となります。

条件： $${r=4}$$ 、$${n=4,\ ...\ ,50}$$ 、試行回数 $${N=10,000,000}$$

図２： n と r/(r-2) - E[k_{r,n}] の逆数の関係 (r=4)

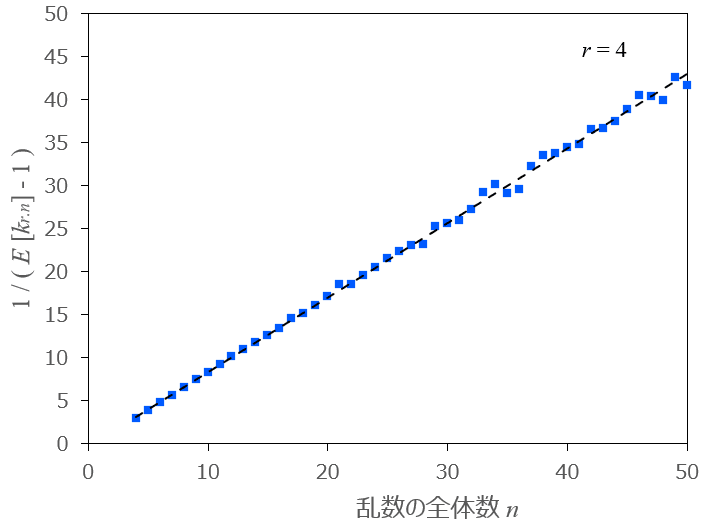
問題点として、[1] と比較して $${n}$$ が大きくなるにつれて近似直線から離れた点が多くなり、計算結果のばらつきが大きくなります。
その影響で、[1] と同様に最小二乗法により $${\dfrac{1}{\dfrac{r}{r-2}-E[k_{r,n}]}}$$ を $${n}$$ の一次式で近似した場合、正確な値を得るためには試行回数をさらに大きくする必要があり、非常に多くの時間を要します。より良い方法が見つかり次第、更新します。

最後に、打ち切り時間を観測値に依存しない特定の値 $${c}$$ とした場合は、$${\dfrac{\hat{m}}{m}=k}$$ の期待値が $${m,\eta}$$ に依存する形となります。
従って、不偏推定量とするための補正係数が未知パラメータの $${m,\eta}$$ を含んだ複雑な関数となり、[1], [2] のように補正係数をかけて不偏推定量とすることは困難です。