量子的な混合状態が現れるのは、人間の無知のせいか？

純粋状態ではなく混合状態にある量子系でも、本当はその系も１つの純粋状態にあるのだが、それがどの純粋状態であるかが分からないだけという説明を聞いたことはありませんか？混合状態は人間の無知が原因だというものですが、そういう説明は実は間違っているのです。

まず１粒子の古典統計力学を考えてみます。混合状態の各時刻の位置と運動量の確率分布は、初期位置と初期運動量を与えて解いた運動方程式の解を使って

という形で与えられます。この場合の純粋状態は各時刻の位置と運動量の値が確定をしている

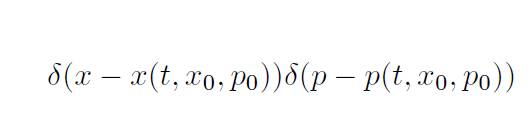
というデルタ関数型の確率分布です。つまり混合状態を含めて任意の確率分布ρは、適当な初期確率分布でこの純粋状態を足し上げた形に書けています。そしてこの純粋状態の重み足し上げは、１つのρに対して唯１つだけ存在するという点が、古典統計力学の重要な性質になっています。この性質を踏まえて、「混合状態は人間の無知を意味するだけで、その対象系は実はただ１つの純粋状態になっている」と言われることが多いのです。

また主観確率と客観確率の区別がおかしくなっている議論も散見します。物理学では、主に客観確率としての頻度的な確率を採用しています。しかしその頻度的な確率でも、観測者依存性はあるのです。２つのサイコロＡとＢがあって、出るその目は必ず同じものになるように設計をされているとしましょう。アリスがＡを観測する前にこっそりとボブがＢの目を見てしまった場合、Ａの目の確率分布はアリスとボブで違います。ボブの結果を知らないアリスにとって、Ａの各目の出る確率は1/6ですが、ボブにとってこれから観測されるAの目は、既に知っているＢの目と同じであり、その目の確率が100%で、他の目の確率は零です。このように確率には観測者依存性があるのですが、同じ実験を何回繰り返しても成り立つという意味で、これは客観的でもあります。つまり頻度的な確率は観測者依存性があっても、再現可能性の観点からは飽くまで客観確率なのです。アリスにとってはボブの結果を知らないために、彼女にとってのAの確率1/6を「人間の無知のため」と表現することは可能です。しかしそれはサイコロ自体が決定論的な運動をすることが起源ではないことに、注意を払ってください。

しかし量子力学になると、この状況は大きく変わります。そのことを２準位量子系を使って説明していきましょう。その量子状態は図１のブロッホ球で表されます。

図１

純粋状態はこの単位球面上の点で表され、また混合状態はその球面の内側の点で表されます。例えばy成分のスピン期待値が零である図２の簡単な場合に注目をしてみます。この場合の純粋状態はx-z平面で原点を中心とした単位円の点になっています。ここで図２のように、大きさが１より小さなスピン期待値ベクトルで記述される混合状態を考えてみます。

図２

このスピン期待値のベクトルは例えば図３の２つのベクトルの確率混合で書けます。

図３

それぞれのベクトルは元のスピン期待値のベクトルに平行です。そして２つとも円周上にその端点がありますので、２つに対応するそれぞれの量子状態は純粋状態です。それを|1><1|と|2><2|と書きましょう。すると元の混合状態の密度行列は、下記のように|1><1|と|2><2|の確率混合として書けます。

仮に混合状態は人間の無知が原因だと考えると、元の混合状態は|1><1|か|2><2|かのどちらか１つの純粋状態に過ぎないことになります。でもこれは本当でしょうか？実は１つの混合状態は異なる純粋状態の確率混合から作られることが知られています。例えば元のスピン期待値ベクトルは、図３のように円周上に端点をもつ３つのベクトルを確率分布qで重みづけることでも生成可能なのです。

図３

円周上の３つのベクトルの対応する純粋状態を、それぞれ|3><3|、|4><4|、|5><5|と書きましょう。すると元の混合状態の密度行列は、次のようにその３つの純粋状態の確率混合としても書けることになります。

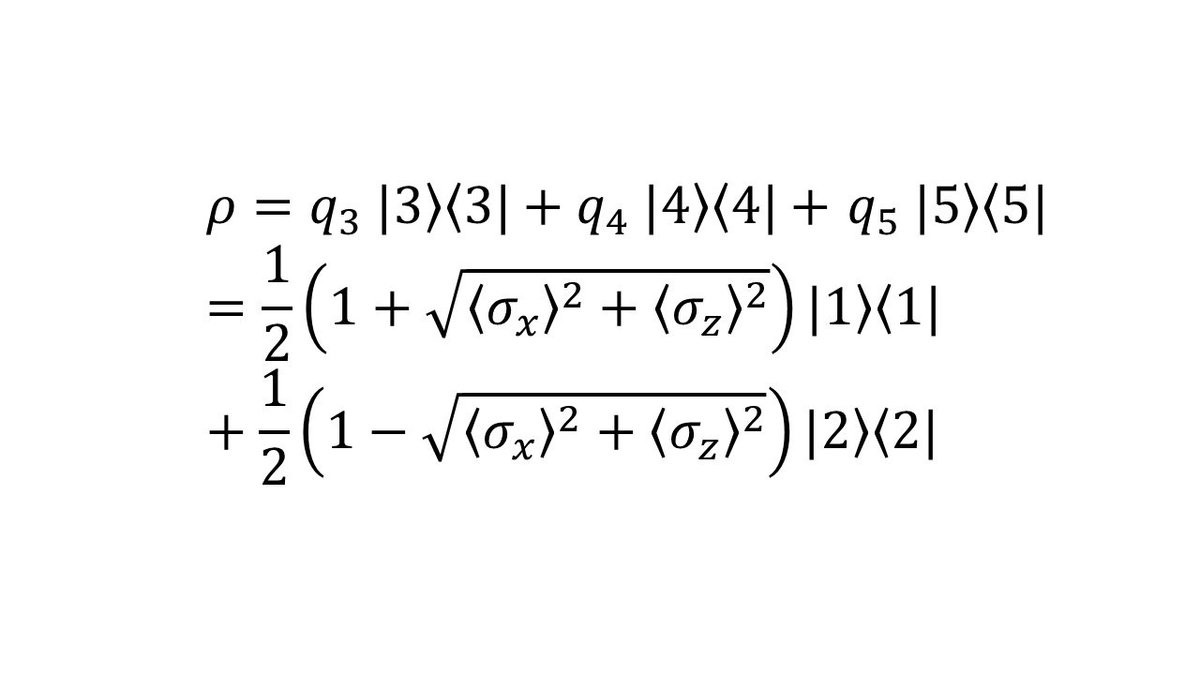
すると上の式のように、１つの混合状態は複数の異なる純粋状態の確率混合で書けます。元の混合状態にある二準位系は|1><1|か|2><2|かのどちらかと考えていましたが、今度は|3><3|、|4><4|、|5><5|のどれか１つの純粋状態だということになってしまいます。そしてこの確率混合による純粋状態への分解の仕方も、無限種類あるのです。この事実から、古典統計力学のように量子系の混合状態の起源を人間の無知のせいにしてしまうことは不可能なのです。つまり混合状態は本当は１つの確定した純粋状態であるという理解は間違いなのです。

しかも量子力学の混合状態には純粋化可能性という性質があります。その量子系の他に外部系を考えると、その合成系全体としては１つの純粋状態としての記述がいつでも可能なのです。それは１つの純粋状態なので、そこには情報の欠如は全く無く、人間の無知が入り込み余地はありません。

例えばDという名前のサイコロとそれを振る実験者D'がマクロな純粋状態にあるという設定を考えてみましょう。実験者は振られたサイコロの目を読みます。すると図４のように実験者の記憶領域とサイコロの目の間に量子もつれをもつDとD’の純粋状態|Φ>が作られます。

図４

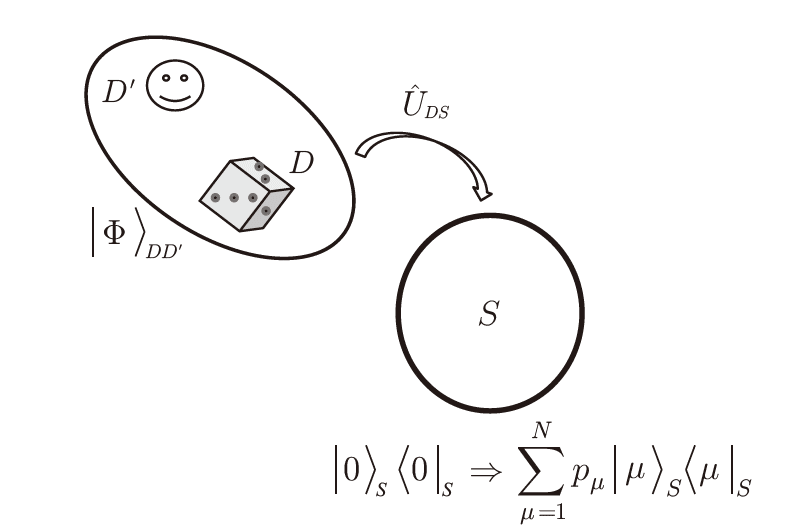
その実験者は６つのサイコロの目に応じて、注目している二準位系Sに純粋状態|μ><μ|を用意します。この過程も合成系全体ではユニタリー操作で行えます。そしてサイコロと実験者を無視したSの縮約状態を計算すれば、N=6として図４のような混合状態でSは記述されることになります。しかしD+D'+Sの全体系は１つに確定をした純粋状態にあります。つまりS系に対する人間の無知が混合状態の原因だったと言うよりも、D+D'+Sの３体系全体でしか実験できないマクロな物理量を測定していないという前提が原因なのです。Sだけの物理量を測れば、Sの状態は計算された縮約状態と区別ができないという意味に過ぎません。D+D'+S系全体の特定の物理量を測定すれば、合成系は純粋状態にあることが確かめられるのです。ですから混合状態は人間の無知によるという説明は、根底から間違っているのです。

なお外部観測者がS系だけを測定する場合には、図４の過程は対象系Sにデコヒーレンスを起こして混合状態にするとも表現できますが、同じ外部観測者にとってD+D'+S系全体にデコヒーレンスは全く起きていないことも、重要です。S系をシュレディンガーの猫とした思考実験でも、実験装置まで含めた合成系全体は１つのマクロな純粋状態にあり、デコヒーレンスによって猫の生死がどちらか１つに決まっているわけではありません。ここにも注意が必要です。このマクロ系の量子状態については『量子情報と時空の物理【第２版】』（サイエンス社）第1章1.4節に書きました。