
ブラックホール時空がもつ熱的なエントロピー
古典的な一般相対論では、ブラックホールは時空に開いた「黒い穴」として描かれ、吸い込まれた物体は二度と外に出られないとされています。しかし、場の量子論を取り入れると状況は変わります。ホーキング博士が指摘したように、ブラックホールは完全に黒いわけではなく、さまざまな波長の光などから成る熱輻射を放つと考えられています。この現象は、現在「ホーキング輻射」として知られています。

熱した鉄から出てくる光の温度を測ると、その鉄そのものの温度が分かるように、ホーキング輻射の温度はブラックホールの温度に等しいと考えられます。(ただし輻射を出すブラックホールの一部分の温度であって、全体の温度であるとは限りません。この可能性については機会を改めてnoteに書こうと思います。)
このように、ブラックホールはもはや温度を持たない時空として理解されるのではなく、温度やエントロピーといった熱力学的性質を持つ存在として理解されることになります。物質を内包するものとして理解されていた時空が、物質のように温度やエントロピーを持つことができるという考え方は、ホーキング博士の理論が示唆したものです。これは、時間や空間に対する全く新しい理解を、理論物理学にもたらしました。
次に、ホーキング輻射の温度はブラックホールの温度と等しいという式を書き、そしてブラックホールの質量Mに光速度の二乗を掛け合わせ、それをブラックホールのエネルギーとします。この結果、ブラックホールはその地平面の面積に比例する、次のような熱力学的エントロピーを持つことが示されます。(以下ではプランク定数ℏ、光速度c、ボルツマン定数を1とする自然単位系で書きます。)
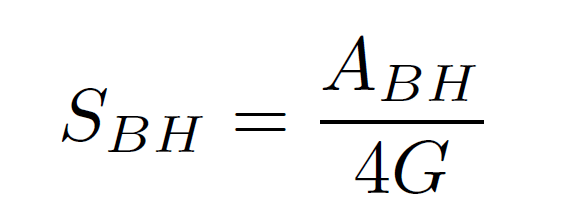
ここでGは重力定数です。このエントロピーは2人の物理学者の名前に因んで「ベッケンシュタイン=ホーキング エントロピー」と現在呼ばれています。一人はもちろんホーキング博士ですが、もう一人はヤコブ・ベッケンシュタインさんです。

ブラックホールの熱力学的エントロピーを提案した頃、ベッケンシュタインさんはブラックホールの名前を付けたジョン・ウィーラー博士の大学院生でした。当時、ベッケンシュタインさんは有名な思考実験を提案します。それは、ブラックホールに熱いコーヒーの入ったカップを放り込むと、そのカップが持っていた熱力学的エントロピーは宇宙から消え去るのか?というものでした。時空が熱的な性質を持つとはまだ考えられていなかった時代に、ベッケンシュタインさんはエントロピーが減少しないという熱力学第2法則を尊重し、ブラックホールはその面積に比例する熱力学的エントロピーを持つべきだと革新的な仮説を提案しました。
当時大学院生だったベッケンシュタインさんのこのアイデアに対し、強い批判をしたのはホーキング博士自身でした。ベッケンシュタインさんは、ブラックホールの面積が決して減少しないというホーキング博士の研究結果を基に、ブラックホールが熱力学的性質を持つと主張したのですが、博士はベッケンシュタインさんが自分の結果を誤って解釈していると考えました。当時のホーキング博士は、時空自体が熱的性質を持つとは考えていなかったのです。
そこでホーキング博士は、ベッケンシュタインさんの仮説が誤りであることを証明しようと計算を始めました。しかし、運命の皮肉が起こります。博士は自分の計算を通じて、ブラックホールが熱的な輻射を放出することを発見してしまったのです。この発見により、ベッケンシュタインさんの仮説は正しいように思えました。さらに、ホーキング博士はエントロピーと地平面面積の間に1/(4G)という比例定数があることを確認しました。現在そのエントロピーは、「ベッケンシュタイン=ホーキングエントロピー(BHエントロピー)」と呼ばれ、広く知られています。
近年では、量子重力理論の研究が進んでおり、超弦理論やループ重力理論を用いて、BHエントロピーを統計力学のエントロピーのように、ミクロな状態の数を積み上げることで部分的に導き出すことが可能になってきています。特に、超弦理論では、特殊なブラックホールの統計力学的エントロピーがBHエントロピーに一致することが示されています。この結果は、超弦理論の成功を示すものとして注目されています。
ただし、超弦理論がBHエントロピーをミクロから導き出したからといって、それが正しい理論であるとは限りません。正しい量子重力理論であれば、BHエントロピーを導かなくてはならないのは確かですが、その逆は言えないのです。
この点は、繰り込み群的に理解できます。超弦理論の研究者であるレオナード・サスキンドは、次のような議論を展開しました。仮にプランクスケールのように非常に高いエネルギーや運動量の領域を正確に説明できる量子重力理論があったとします。それが超弦理論であるか、ループ重力理論であるか、または未知の理論であるかは分かりません。いずれにせよ、何らかの量子重力理論が存在すると仮定します。
一方、現在までの観測や実験では、プランクスケールよりはるかに低いエネルギーや運動量の領域では、アインシュタインの一般相対論が正しい記述を提供していることが知られています。したがって、量子重力理論は必ず低エネルギー領域でアインシュタインの理論を導く必要があります。繰り込み群的な説明によれば、高エネルギー領域での自由度を積分した結果、得られる低エネルギーの有効理論が一般相対論のアインシュタイン=ヒルベルト作用でなければならないのです。さらに、低エネルギー領域では、重力定数Gが作用の中に現れる必要があります。高エネルギー領域での複雑な量子効果は、低エネルギー領域ではGの繰り込み効果に吸収されるのです。
もう少しだけ具体的に考えてみます。正確な量子重力理論は、温度の逆数パラメータβの分配関数がなんらかのミクロな自由度uを使って下記のような経路積分で定義されているとしましょう。
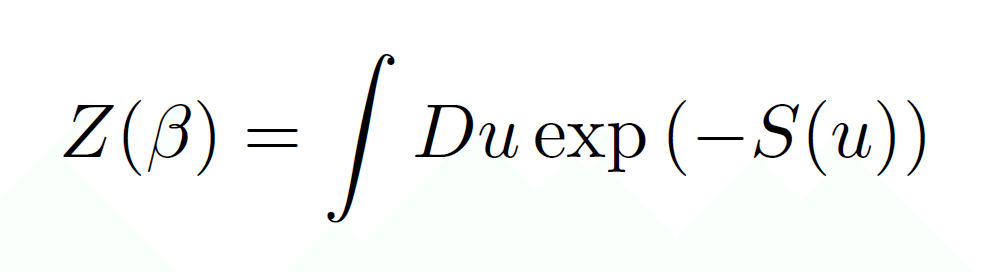
この経路積分の積分パラメータを運動量pのモード自由度u(p)に分解できるとして
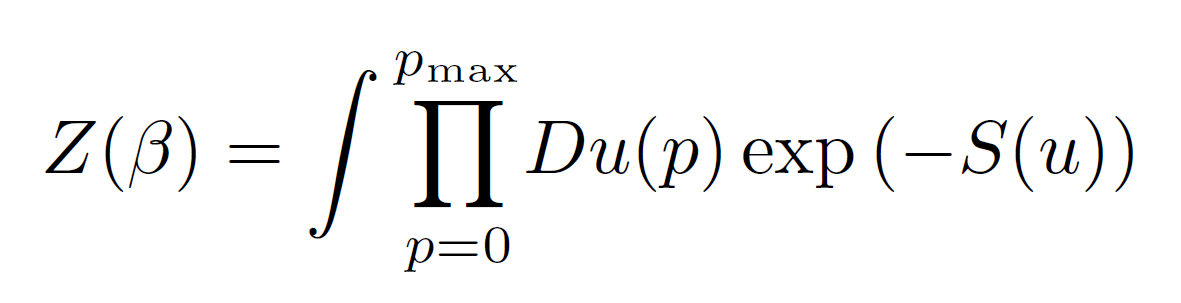
と書きます。この式では運動量に上限があるように書いていますが、そのような上限が無くても良いです。高い運動量モードの積分を実行してしまい、低い運動量のモードに対する経路積分を下記のように残します。
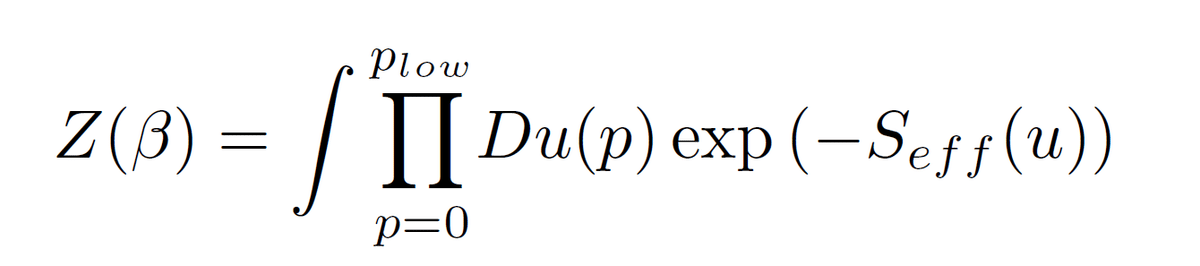
この時に出てくる有効作用では、高い運動量モードの量子効果は全て繰り込みとして、その低エネルギーの相互作用の結合定数に含まれてしまいます。
そしてこの低エネルギー経路積分は、有効理論として観測や実験から下記のような一般相対論の経路積分になるはずだというのが、サスキンドさんの議論の肝です。
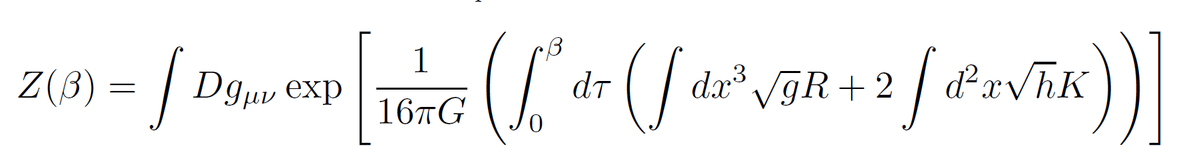
重力定数Gは低エネルギー領域で計測されますので、この有効作用の中の結合定数を用いて理論的には定義をされます。作用の第1項目は有名なアインシュタイン=ヒルベルト作用になっていますが、第2項目に表面項が付いています。この表面項は、重力相互作用が長距離力を出すことが原因で現れます。この表面項の具体形には不定性がありますが、この表面項の役割はどれでも共通です。体積項であるアインシュタイン=ヒルベルト作用の変分をとってアインシュタイン方程式を出すときに、表面領域から運動方程式の解を不要に狭める余分な条件が出てこないように、この第2項目の表面項が調整をしてくれます。
このような有効作用が現れるというサスキンドさんの自然な仮定を信じると、(2)式の経路積分は下記のように評価されます。(なおこのあたりのユークリッド経路積分での計算自体は、サスキンドさん以前にホーキング博士と彼の共同研究者によって既に行われていました。サスキンドさんの議論は、その計算に繰り込み群的な意義を与えたものです。)
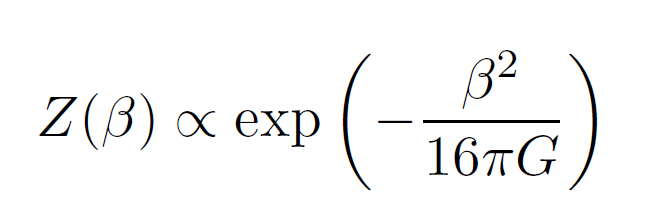
ここでβはブラックホールの質量と下記の関係が成り立つことも、経路積分の鞍点法の議論から示されます。
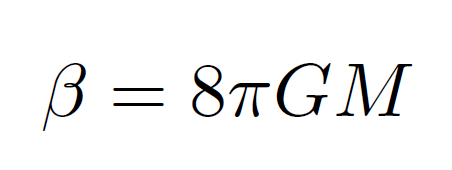
ブラックホールの質量Mからは、その地平面の半径が下記のように得られまます。
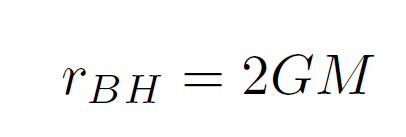
そして地平面の面積も下記で与えられます。
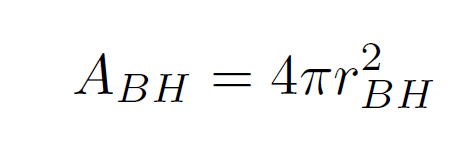
従って地平面の面積をβの関数として与えることが可能です。ここで分配関数Z(β)から熱力学的エントロピーを計算すると、(3)式から下記のようにちゃんとBHエントロピーが導かれます。
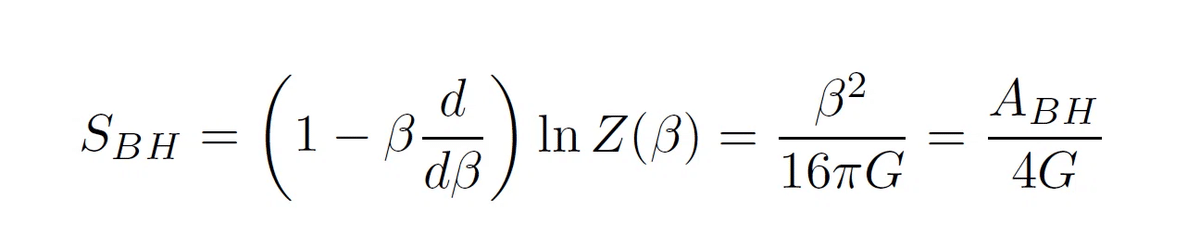
この結果を得るのに、サスキンドさんは量子重力理論の詳細を使っていません。超弦理論とかループ重力理論とか指定をせずに、これを導きました。従ってBHエントロピーを導くことは、正しい量子重力理論の必要条件に過ぎず、特定の量子重力理論の正しさを保証する十分条件ではないのです。
いいなと思ったら応援しよう!

