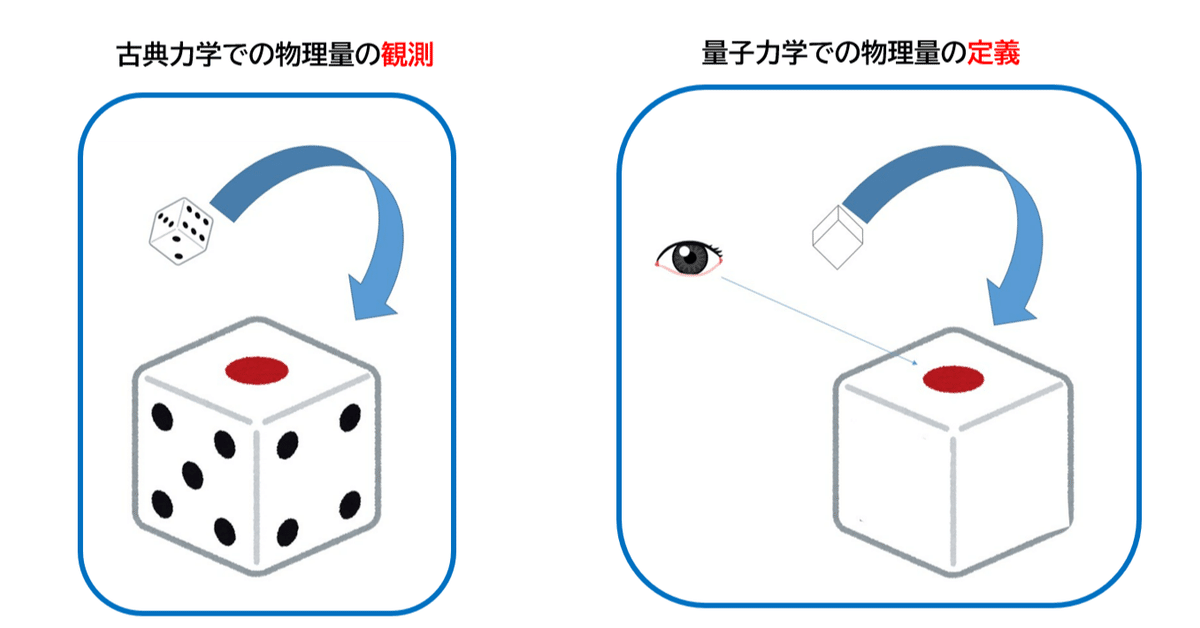
量子力学において物理量を定義するとは?:「堀田量子」第2.5章
おかげ様で多くの方からご好評を頂いております、通称「堀田量子」の拙書ですが、第3章における物理量の操作的な定義についてわかりにくいというご意見が一部ありました。執筆時には厳しいページ数制限があったため、初版では詳しく説明ができませんでしたが、その正しい理解のための補助線として、第2章と第3章を繋ぐ位置づけの「第2.5章」を、ここに書いておこうと思います。
2.5-1節 操作的に定義される物理量の考え方
本書は、前期量子論や正準量子化を論理の基盤とした前世紀の教科書とは異なる構成を採用しています。そのため、従来の教育を通じて培われた先入観を持ったまま読み進めると、ギャップを感じる場面が多々あるかもしれません。
その代表的な例が、「物理量を人間が操作的に定義する」という点です。「物理量や、その値とは、人間が測ろうと測るまいと、測定以前から厳然と実在するものではなかったか?それを人間は単に観測するだけでは?」と疑問に感じられる方もいるでしょう。
正準量子化を採用している従来の書籍では、「物理量はエルミート行列(またはエルミート演算子)である」といった表現がよく見られます。この抽象的な演算子は、物理的には何がなんだかわからないが、少なくとも測定以前からそれは実在してそうだと、読者に感じさせてしまいます。それを観測しているのが量子力学の測定だとか、更に量子力学はその抽象化された「演算子」という実在対象を扱う理論という誤解を生む可能性もあります。
実際には、量子力学の物理量の値は、測定前に実在していないことが、ベル不等式の破れの実証から現在分かっています。ですから「人間が測定する前からあったものを、人間が観測するだけ。」というのは、間違った観方です。これを解消するためにも、本書は書かれました。
まず、量子力学に進む前に、力学や熱力学において「物理量」とは何だったのかを振り返ってみることが有益かと思います。例えば、「温度」という物理量を考えてみましょう。温度は「熱い」「冷たい」を定量的に区別する量だと多くの人が認識していますが、物理学的には温度がどのように精密に定義されるのかについては、現在でも様々な議論が続いています。
歴史的に見れば、温度計の発明が実証科学における大きな出来事でした。熱平衡にあると考えられるお湯やその他の物体に温度計を当てると、温度計はある値Tを出力します。その目盛りは、当時の科学者が最良と考えた方法で数値を割り振ることで決められていました。例えば、素朴なイメージとしては、一定火力を持つ熱源で水を温める場合、加熱時間が2倍であれば温度の上昇も2倍になるといった感覚に基づき、温度計の目盛りを設計します。
一旦温度計で温度Tの値が実験から読み取られると、同時に温度の関数である様々な物理量もその1回の実験から値が決まります。例えば熱的な内部エネルギーは、この系で許されるエネルギー値全体を知っていれば、Tの関数です。

ですからこれも温度の1回の測定で、T以外に得られる物理量となります。一般化すると、たった1つの温度計で、1回温度を測ってしまえば、温度以外に任意のTの関数f(T)で与えられる物理量も、その測定でわかってしまうのです。温度Tは温度計の測定で定義される量とみなすと、同様にその温度計の測定でf(T)も定義される物理量とみなすことが可能です。このような見方は、量子力学でも同様に使えます。
こうして、一つの基準となる温度計の設計が定められ、それを用いて様々な物理量を操作的に測定する手法も発展しました。これは特殊相対論での光を用いた時刻や距離の定義でも同じです。このように、物理量は測定機やその設計に依存した「操作的な定義」に基づいて理解されることが多いのです。
ただしその定義法で一意となった物理量を、この定義に使われた実験法ではない、別な実験法で改めて測定することも、物理学では頻繁に行われます。得られる物理量の値やその確率分布が元の実験法での結果に一致すれば、その別な実験法で測られた物理量は、先の基準的な実験法で定義をされた物理量そのものであるとみなすことになります。
2.5-2節 量子力学の物理量も「物理操作+基準測定」で定義される
『堀田量子』でも、温度の定義のように、「基準測定」と呼ばれる一つの測定を用いて、操作的に対象系の様々な物理量を定義するという思想に基づいて書かれています。この基準測定に用いる装置は、熱力学における温度計と同様の役割を果たします。基準測定を起点に物理量を定義することで、抽象的な理論を具体的な測定に結びつけ、より明確に物理現象を理解するアプローチが採られているのです。
第2章や第3章で考察されている量子的な対象の測定は、対象系に対する「物理操作+基準測定」によって構成されています。実際の実験において、このような操作によって得られる装置からの出力は、対象系の準位数に応じて異なります。たとえば、二準位系では2つ、三準位系では3つの出力が得られます。
具体例として、スピン粒子のシュテルン=ゲルラッハ(SG)実験を挙げると、装置から出てくる粒子ビームの本数は、二準位スピンの場合は2本、三準位スピンの場合は3本です。この場合の基準測定は、z軸方向に向けられたSG装置で行う測定を指します。
2.5-3節 量子力学の公理系を満たすものが「量子系」
第2章では、二準位スピン粒子のSG実験から得られる確率分布のデータを用いて密度行列を定義し、この密度行列がボルン則や状態の重ね合わせといった量子力学の基本的な性質を持つことが説明されています。その後の章を読み進めることで、このスピン粒子が以下の量子力学の公理系を満たすことも明らかになります:
量子状態は密度行列で表現される。
物理量はエルミート行列に対応する。
エルミート行列の固有値が、実験で観測される物理量の値である。
観測される物理量の値の確率は、ボルン則に従う。
密度行列の時間発展はシュレディンガー方程式で記述される。
この5つの公理が実験で確かめられた系のことを、通常「量子系」と多くの教科書では呼ばれます。本書でも、これを「量子系」という用語の定義をしています。
ここで1番目の公理に現れる「量子状態」は、SG実験の確率分布の結果を説明するための最小限の情報として定義されています。この定義は、あらかじめ粒子の位置座標や運動量のような物理量としての「状態」が与えられているとする古典力学的な考え方と大きく異なります。
2.5-4節 二準位スピン系のシュテルン=ゲルラッハ実験での物理操作
第2章ではスピン粒子そのものを回転させるのではなく、SG装置を特定の方向に回転させた後にスピン粒子を入力し、確率分布を測定する手法が説明されています。これは「対象系に対する物理操作+基準測定」というスキームから一見外れているように見えるかもしれません。しかし、空間の回転対称性を認めると、この実験は能動的操作(active operation)の実験とみなすことが可能です。具体的には、回転したSG装置から得られたデータを、スピン粒子に逆回転操作を施した後でz軸方向のSG装置を用いて基準測定を行った結果として再解釈することができます。この能動的操作の観点に基づけば、粒子に回転という物理操作を施してから基準測定を行うことで、第3章で示されるように任意のエルミート行列に対応する物理量の測定を定義できることになります。
また、第6章6.5節で述べられているように、スピン粒子をSG装置に入れる前に一定方向の一様磁場を加えることで、スピン粒子自体を能動的に回転させることも可能です。このように、SG装置を回転させる受動的操作による実験も、粒子に磁場をかける能動的操作による実験も、「物理操作を対象に施してから基準測定を行う」という一般的なスキームの例として理解されます。
対象を加熱して熱平衡に達した後に温度計で測定することで温度を定義するように、二準位系の物理量も「物理操作+基準測定」によって定義される概念と見なせるのです。これが本書の基本的な思想となっています。
2.5-5節 古典力学的な物理量概念の崩壊
もしスピンが古典粒子のような自転運動を起源とするものであれば、ここまで複雑に考える必要はありませんでした。しかし、第1章1.2.2節で説明されている方向量子化という現象によって、この古典的な自転運動の描像は破棄されます。スピンに対する古典的なイメージが成り立たないという事実は、従来の素朴な物理量の概念も瓦解させました。特にベル不等式の破れの実験結果は、測定前にスピンの値そのものが決まっているとは考えられないことを意味していたため、多くの人々を驚愕させました。そのため、新たに操作的な方法でスピンやその他の量子的な物理量を定義する必要性が生じたのです。
2.5-6節 同時測定可能な物理量
次に前世紀の量子力学の教科書にもよく出てくる、同時測定可能な物理量について考えておこうと思います。正準量子化での量子力学の導入では、そもそも何故物理量がエルミート行列で書けるのかは全く不明であり、一種の神秘性さえも多くの人に感じさせていました。物理量の存在自体を理論のスタートに置きたいと考える前世紀的な感覚では、そう感じてしまうのも避けがたいかとも思えます。その「物理量であるエルミート行列」在りきの前提において、行列が可換である2つの物理量は、同時測定可能であるとも書かれているのです。正準量子化で学ぶと、この直観的意味すらわかりません。

しかしこの同時測定可能性は、深遠な真理とか考える必要もなく、簡単に理解できることなのです。量子力学とも直接は関係ありません。以下では第3章で扱うN準位系のうち、N=3の三準位系を例にして説明をしていきます。
まずエネルギー(ハミルトニアン)などの物理量の値を実験で1つ得た場合、その実験データからは、その物理量に任意の関数を適用して定義される拡張された物理量の値も同時に得られる点が重要です。これについては、下記記事も参照してください。
熱力学系で温度Tが測定で分かれば、他のf(T)という物理量も同時に測定されたように、三準位系の任意の物理量Aについて、実験で得られた3つの値を関数f(x)によって変換すると、対応する物理量f(A)の値も自動的に決まります。ここで、関数fは自由に選ぶことができ、例えば脈絡なく f(1)=−1、f(2)=π/2、f(3)=e(ネイピア数)と定義することも可能です。この場合、Aの出力結果を次のように定義してみます。1番目の出力に対してA=a(1)=1、2番目に対してA=a(2)=2、3番目に対してA=a(3)=3という値を割り振ります。このようにして物理量Aを定義すると、f(A)は各出力結果に対して以下の値を取るように、一意に決定されてしまいます。

このf(A)を便宜上、Aとは別な物理量として、新たな物理量Bと定義すればよいだけです。
この部分は単なる定義の仕方に過ぎないため、行列表示を用いた議論は必要ありません。しかし、この記事の最後で述べるように、量子力学の確率分布として記述された結果を行列表示に変換すると、B=f(A)という定義が(1)式におけるAとBのエルミート行列が可換である条件と一致することが分かります。したがって、「行列が可換であることが同時測定可能の条件である」と言われても、それを難解なものとして恐れる必要は全くありません。
2.5-7節 同時測定可能な物理量の具体的な定義例
もう少し図を用いて説明してみます。三準位系の基本測定を行う測定装置に連続的に対象系を入力したとき、k=1,2,3の区別可能な異なる結果が出ている状況を下図に表しました。

1つの対象系を装置に入力したとき、その1つがk=1として出力をされた場合が下記です。

同様に1つの対象系を装置に入力したとき、その1つがk=2として出力をされた場合が下記であり、

また1つの対象系を装置に入力したとき、その1つがk=3として出力をされた場合が次の図になります。

上の図では測定機のモニターはそれぞれのkの値が表示されていますが、ここで簡単ですが重要なのは、任意関数f(x)を用いてf(k)という値も同時にこの1回の測定で得られていることです。例えばkの2次や3次の積なども測れていますし、exp(-k)やcos(πk/2)も測れています。そしてk=1として出力をされた場合に、その結果をモニター上に表示したものが下図です。

同様のことをk=2とk=3で描いたものが下の図となります。


これからわかることは、温度計の時と同じように基準測定でも多数の物理量を操作的に定義できるという事実です。本書でN=3とした場合には、各kの結果に対してゲルマン行列の2つの対角行列のk成分によって、下記のように物理量を定義しています。


つまりk=1の場合には、下図のように、測定機のモニターにはその2つの物理量の値が表示されます。

同様に、k=2,k=3の場合の図も下に描きました。


ここで繰り返し強調をしておきますが、モニターに映る2つのゲルマン対角行列の各対角成分は、単に観測されたkの値から計算されたものであり、この測定機の中には、このゲルマン行列の物理量のために特化された、作り込みの装置はありません。これが「ゲルマン対角行列の物理量を操作的に定義する」の意味となります。
2.5-8節 二準位スピン系に潜むSU(2)群構造を証明したSG実験
第2章でボルン則や状態重ね合わせを導いた重要な実験結果は、(2.5)式のスピン期待値のベクトル性でした。SG装置が向いている方向の単位ベクトルを

と書くと、(2.5)式は下記のようになっています。

この実験事実は、この二準位スピン系にSU(2)という群構造が入っていることを意味しています。つまり

という2次元ユニタリ行列を定義すると、これに対応した密度行列の操作を

で与えれば、

からスピン期待値のベクトル性が出てきます。なお一般にユニタリ行列に対応する物理操作のことを、「ユニタリ操作」と呼びます。
逆に任意の初期密度行列でスピン期待値のベクトル性が成り立てば、下の関係式が導かれます。

これをSU(2)関係式と以下では呼びます。ここで下記のようにSU(2)固有の実係数を

定義すると、このSU(2)関係式は

と書き換えられ、SU(2)行列とパウリ行列の間の数学的関係式を得ます。これをスピン行列のベクトル性関係式と呼ぶことにします。なお本書(2.44)式の行列から全体の位相因子を落とした任意のSU(2)行列も、3つのオイラー角で定義されるx軸回転操作とz軸回転操作に対応するユニタリ行列によって、下記のように書かれます。

x軸回転操作とz軸回転操作のユニタリ行列の具体形については、本書第12章を参照してください。この任意の2次元ユニタリ行列に対しても、スピン行列のベクトル性関係式はもちろん成り立ち、SG実験のデータには、完全なるSU(2)構造が現れていることも判明します。
本書(2.5)式のスピン期待値のベクトル性関係式から、前述の議論に出てくるスピン行列のベクトル性関係式においても、ユニタリ行列を任意のSU(2)ユニタリ行列にできる点はとても大事です。そしてこの関係がSG実験の実験データに現れていたことに注目をしてください。つまりこの系の実験データにはSU(2)が隠れていたのです。以下の節では、三準位系を考えるときに、これに対応する或る2本の拡張関係式と、それを実験で確かめる測定プロトコルを具体的に与えます。この2本の関係式が実験で証明されれば、三準位系で定義される密度行列に対して、その実験データからボルン則と状態重ね合わせが演繹されます。
2.5-9節 二準位系から三準位系へ
この稿は第2章と第3章を繋ぐスロープとして書いているので、以下では第3章の内容に当たる内容をN=3の場合に説明をして、上で述べてきたことと繋げて行こうと思います。この辺りの大部分の内容は既に下記にても扱っています。
2.5-10節 反復可能性をもつ三準位の基準測定
まず扱いたい三準位系において、反復可能性を有する基準測定が実験的に構成できたとします。反復可能性とは、その測定はその直後に同じ測定を繰り返しても、一回目と二回目の結果は変わらないことを指しています。

図1では基準測定の概念図を描きました。左からくる青い直線は、この測定装置に入力する、或る状態の対象系を表しています。そして黒い箱が測定機です。測定機からは青い線で描かれる3つ状態の対象系が出力しており、その対象系の状態はその測定で観測されるそれぞれの確率で生成されています。
2.5-11節 三準位の中に含まれる量子ビット
基準測定の3つの状態のうち、図2のように特定の状態の系の入力に対して1番目と2番目の状態の系しか出力しなかったとしましょう。この場合は二準位系として考えることができます。そしてこの二準位系が「二準位系量子力学」の公理を満たすことは既に実験で検証済みという前提で話をします。

この場合は、1つの量子ビットがこの対象系の中にあると言えます。そしてこの系に対する或る物理操作は、この量子ビットに対するユニタリ操作であることが、二準位系の量子力学の公理(前提)から要求されてきます。(教科書第6章に書いてあるように、ユニタリ操作以外の物理操作ももちろんあるのですが、ここでは任意のユニタリ操作の実装可能性だけを仮定すればよいです。)この状況を図3で描いています。

この二準位も量子ビットであるという前提をすると、この二準位ユニタリ操作には対応する下記の2次元ユニタリ行列があるはずなので、その行列をこの操作1つ1つを区別する「名前」として使用をしましょう。

ここで状態ベクトル|1>は1番目の状態に対応し、|2>は2番目の状態に対応しています。そしてその2つのベクトルは互いに直交をしています。そしてその成分表示では3次元ベクトル空間の元としても書こうと思えば、書かけます。(ただしそのままだと(2)式の行列は3次元の意味でのユニタリ行列にはなりませんが。)また異なるユニタリ操作が区別できれば良いので、この2次元行列も3次元的に表記しても実質変わりません。そこで図4のように、1番目と2番目の状態から作られる量子ビットに対する各ユニタリ操作に、3次元ユニタリ行列での名前も付けておきましょう。

ここで|3>は|1>と|2>という2つのベクトルと直交をする単位ベクトルです。この3次元ユニタリ行列は、今は関係のない第3番目の状態に対しては何も影響を与えない行列になっています。
次に2番目と3番目の状態に注目をします。この2つの状態も二準位系ですが、この二準位系も「二準位系量子力学」の公理を満たすことを既に実験で検証済みという前提にします。つまり図5のように別な量子ビットがこの系に現れています。

この量子ビットに対しても図6のような二準位のユニタリ操作が存在するはずです。

このそれぞれの二準位ユニタリ操作にも、(3)式の2次元ユニタリ行列が1つ1つ対応しているはずです。

ここで状態ベクトル|2>は2番目の状態に対応し、|3>は3番目の状態に対応しています。この2つのベクトルは互いに直交をしています。また3次元ベクトル空間にこの2つのベクトルを埋め込めば、|1>とも直交をしています。またこの2次元ユニタリ行列も、図7のように自明に3次元化できます。

そこで2番目と3番目の状態に対する各ユニタリ操作に対して、この3次元ユニタリ行列をその名前とします。
2.5-12節 連続する二準位ユニタリ操作で定義されるユニタリ操作
ここまで、図2と図5の2つの量子ビットの二準位操作の名前付け(即ち二準位ユニタリ操作と、3次元ユニタリ行列との紐づけ)が終わりました。これらから構成される物理操作はまだ他にもあります。例えば図8のように、一般の初期状態にある対象系に最初に図6の操作を対象系に施し、出力された対象系に連続して図3の操作を施すのです。

この図8の操作にも、3次元ユニタリ行列の名前を付けることができます。それは図9のように、図4と図7の3次元ユニタリ行列の積を対応させるのです。

勝手に与えられた3次元ユニタリ行列は、物理的には意味を持たない位相因子を除いて、必ず一意にk=1とk=2に対応するユニタリ行列と、k=2とk=3に対応するユニタリ行列の積に分解できます。ですから、図9のように操作の名前を定義しても、その3次元ユニタリ行列からどんな図3と図6の操作なのかが問題なく読み取れます。
なお以下で考える物理操作は図8の操作だけとします。この実験ではカバーできない高エネルギー領域では可能となるかもしれない新たな物理操作の可能性は考えません。この妥当性は、今考えている実験のエネルギー領域や実際の実験結果からチェックすることもできるので、そのチェックは済んでいるとここでは仮定して、話を進めます。
2.5-13節 三準位系での物理量の操作的定義
ここまで来ると、「ユニタリ操作+基準測定」という操作で、三準位系の物理量を定義することが可能となります。今は図3と図6の任意の二準位ユニタリ操作が存在しているので、図9の3次元ユニタリ行列も任意にとれます。この行列で書かれる三準位ユニタリ操作を対象系に施した後に、図1の基準測定をして、3つの各出力状態が観測される確率分布を実験で求めます。物理量Aの値として1番目の結果ではA=a(1)と勝手に割り振り、それを定義値とします。2番目ではA=a(2)、3番目ではA=a(3)と定義するのです。そしてこの手順自体が同時に「Aの測定」の定義にもなっています。温度のように、この測定プロトコルで計測されるものが、任意の初期状態にあるこの対象系の物理量Aの定義だとするのです。
ここで重要なこととして以下のことに注目します。このAを測るプロトコルの一連の操作は、下記で定義されるエルミート行列から、少なくとも固有値に縮退がない場合には、一意に読み取れます。

エルミート行列の固有値に縮退がある場合は、そのエルミート行列を対角化するユニタリ行列は一意ではないですが、対角化できる1つの行列を定義として選べば、縮退がない場合と同じです。どちらにしろ、先にこの3次元エルミート行列が与えられれば、それを対角化する3次元ユニタリ行列が、「ユニタリ操作+基準測定」の「ユニタリ操作」を指定し、その固有値が「基準測定」での各出力に割り振られた物理量の定義値だと、一意に読み取れます。ですので、任意の3次元エルミート行列は、「ユニタリ操作+基準測定」の操作で定義される物理量を、曖昧さなく指定しています。そしてこれが従来言われていた「量子力学の物理量はエルミート行列である」ということの正確な意味となります。
2.5-14節 ゲルマン行列に対応する物理量の導入
この3次元エルミート行列の中には、下記の8個のゲルマン行列も含まれています。

ですからこの8個の行列も、それぞれ「ユニタリ操作+基準測定」という或る測定プロトコルを意味しています。つまり対象系にそのユニタリ操作を施して、基準測定をすれば、このゲルマン行列の物理量が測定されるのです。
なお最初の2つのゲルマン対角化行列は、二準位系の基準測定で使ったパウリ行列のz成分の拡張として重要となります。
2.5-15節 拡張された「スピン期待値のベクトル性」
物理量の定義が済みましたので、以下では三準位系の量子力学を実験データから構築していく方法を説明していこうと思います。第2章の二準位スピン系では、「スピン期待値のベクトル性」の関係式が量子力学の公理を満たすためには重要でした。この関係式が実験で破れていれば、その系は決して二準位系の量子力学の公理を満たさないことが確定します、またこの関係式が実験で成り立っていることが確認されれば、第2章で定義された2次元密度行列は、ボルン則と状態重ね合わせを満たすことも証明されました。
ですので三準位系でも同様に、三準位系量子力学の公理が成り立つか成り立たないかを判別できる、「スピン期待値のベクトル性関係式」の3次元版拡張関係式を与えます。その実験設定は図10に描かれています。

この実験全体は、「ユニタリ操作+基準測定」で構成されている合計10個の実験から構成をされています。最初の8個の実験では対象系には何も物理操作をせずに、8個のゲルマン行列に対応する物理量の測定をします。そして各物理量の期待値を実験データから算出します。次に図8で定義される任意のユニタリ操作を対象系に施したあとで、基準測定でゲルマン行列の最初の2個だけ測定します。そしてその期待値をデータから算出します。
これで合計10個の物理量の期待値を実験から得ました。そしてここがポイントとなるのですが、これらの期待値が下記の(5)式の2本の関係式を満たさなければ、その対象系が三準位系量子力学の公理を満たすことは絶対にありません。そしてこの(5)式が実験で成り立てば、必ずその系でボルン則と状態重ね合わせが出てくるのです。

この右辺に現れている係数は、左辺の2個の物理量測定に使ったユニタリ操作の行列とゲルマン行列を使って、下記の式で与えられているものです。

なおこの係数が実数であることも、下記の行列計算からわかります。

この(6)式の係数は、数学的にはSU(3)群論の下記の(7)式の性質を満たすことが知られています。(5)式は二準位スピン系でのスピン期待値のベクトル性関係式の自然な拡張になっています。

2.5-16節 3次元密度行列の定義
さて次に(5)式を10個の物理量の期待値が満たすことを実験で確認できたとしましょう。このときに後半の8個の物理量(Uの操作をしないで測定した物理量)の期待値を使って、下記の式で3次元密度行列を定義します。

この(8)式は、量子情報理論において量子状態トモグラフィの式として知られています。
2.5-17節 スピン期待値のベクトル性の拡張関係式からボルン則と状態重ね合わせを導く
この密度行列はゲルマン行列の物理量の期待値をきちんと再現します。

この(9)式を(5)式の右辺に代入することで

という関係が出ます。そしてこれと(7)式を使って以下の計算をします。

一方で、(5)式の左辺に出てくる「ユニタリ操作+基準測定」で測定されたゲルマン行列の最初の2つの物理量の期待値の元となる各状態の出現確率は、k=1,2,3として

とも書けます。(11)式は2本の期待値の定義式と、全確率は1であるという条件式の合計3本の自明な方程式を解くことで確認できます。つまり

という3本の式を解いて

という得られた答えを1つにまとめたものが(11)式です。この(11)式の右辺に(10)式を代入することで、

と書けますが、さらにこれは

と変形できます。そしてトレース内部の行列の円巡回対称性を用いて

とまとめることが可能です。ここで

という関係式、つまり

を(12)式の右辺に代入することで、最終的に以下のボルン則を得ます。

これは初期状態を表す密度行列に3次元ユニタリ行列で表される物理操作を施した後、基準測定をすると、(13)式のボルン公式でその確率が計算できることを意味しています。特に初期状態を基準測定の1番目の出力状態にとれば、

が成り立っています。ここでこの3次元ユニタリ行列は任意で良いので、

という式で、任意の複素単位ベクトルが得られます。この操作の後には、基準測定の1番目の出力状態は任意の単位ベクトルで書かれる純粋状態になっていることが分かります。そしてその純粋状態を準備したユニタリ操作の後に連なる、2回目の基準測定をしたとき、その3つの出力状態のうちk番目の状態が観測される確率は、(14)式と(15)式から

という形にまとまります。これはまさに純粋状態に対するボルン則そのものです。(15)式の状態ベクトルには任意の3次元単位ベクトルが許されているため、元の基底ベクトルでこれを下記のように展開することができて、その結果として三準位系での量子力学の状態重ね合わせの存在も導かれます。

2.5-18節 N準系でも同じ
ここでは三準位系を例にして紹介しましたが、これを一般のN準位系にしたものが第3章の基本的な内容となります。そしてこのことが、ページ数制限のために簡略化して教科書第3章に書かれている「たとえ未知のN 準位系でも、任意のU (N) に対応する物理的な操作は実現可能だと考えよう。ただしこの前提は、飽くまでも各系において、実験で検証されるべきことである。」という部分の、N=3とした場合の具体的な内容です。物理学は実証科学ですので、任意のユニタリ行列に物理操作が対応するという前提も、それを実験で検証できる方法論を述べないといけませんが、それは上で説明をしてきたように、とても非自明なことであり、当たり前のことではありません。
2.5-19節 第15章のテーマと第3章のテーマは、違うもの
また実験ではなく、なんらかの自然原理だけから量子力学の公理系を導出する話は、この第2章と第3章のテーマではありません。それは重要な未解決問題として第15章で説明をされています。それを意識せずに、第3章の議論には致命的な誤りがあるという主張をされる方も居ましたが、それはきちんと本書の主張を理解できていないための誤解に過ぎません。
2.5-20節 同時測定可能性、ふたたび。
最後に可換な行列に対応する2つの物理量は、同時測定可能だという話に戻り、それを説明することで、この「第2.5章」を終えたいと思います。
「ユニタリ操作+基準測定」で測られる物理量Aには(4)式で定義をされたエルミート行列が対応しています。そしてf(x)という任意関数を使って定義をされるf(A)という物理量には、下記で定義をされるエルミート行列が対応をします。

この定義から、

となり、2つの行列が可換であることも自明です。そして(1)式の可換性を満たすエルミート行列をもつ物理量Bも、或る関数f(x)を選ぶことで、

のように実現しているのです。ですから(1)式を満たす2つの物理量が同時測定可能なのは、当たり前なのです。
(補足:もしAの定義値の中の一部の数値が重なっていて縮退があるときには、Aに対応するエルミート行列の任意関数を考えても、Aの行列と可換なBの行列はAの行列の関数では書けない場合があります。しかしその場合でも、定義値に縮退のない物理量Cが必ず存在して、AとBの行列の両方が下記のようにCの行列の関数で書けることが知られています。このCの行列は、もちろんAとBの行列とも可換です。

ですからAの定義値に縮退があろうとなかろうと、交換可能な行列に対応する2つの物理量AとBが同時測定可能なのは、物理としては極自然なことなのです。)
2.5-21節 蛇足
最後に蛇足ですが、コメントを加えておきます。必要のない方は読み飛ばしても大丈夫です。物理理論では、どんな対象でも、それを測るどんな測定でも、エネルギーやその時点での技術などで決まる適用範囲があります。例えばSG実験ではスピン二準位系とみなされる銀原子や中性子のSG実験でも、それらの粒子の内部構造(銀原子は原子核と47個の電子という内部構造をもち、中性子は3つのクォーク粒子とそれを繋ぐグルオン粒子という内部構造をもつ)の励起が無視できる低エネルギーでの実験です。その実験領域では二準位ですが、もし粒子を測定するときに、高いエネルギーを粒子の内部構造に注入してしまう装置で物理操作を行うと、スピンの組み換えが内部で起こってしまいます。その励起状態のまま粒子をSG装置に通せば、多準位スピン状態が観測されます。低エネルギーの操作とSG実験だけならば二準位だったものが、例えば三準位などで記述される必要があります。もしエネルギーがそれほど高くなく、SG装置を通過するころには増えた準位はもう見えなくなって、SG装置からは2つの粒子ビームしか出てこない場合もあり得ます。測定結果として2つの状態ですが、SG装置に入る前の中間エネルギー領域で、光子を出したり、別な測定機と接触をしていれば、その測定結果も使ってなんらかの一般確率論の二準位版で解析できることもあります。
また付録Gの隠れた変数理論の棒磁石モデルも、SG実験のエネルギー領域では二準位で記述され、その実験データから第2章のように2次元密度行列が定義可能です。そしてボルン則や状態重ね合わせが出てきます。しかし棒磁石モデルの「棒磁石」が本当に実在すると仮定をすると、高エネルギー領域で状況は変わり得ます。量子力学の公理を満たすのにその棒磁石モデルの中では必要だった「謎の揺らぎ」もミクロに観察できる高エネルギー領域では、系としては二準位どころか、もっと多数の自由度、そしてそれを測定する装置や対応する測定のPOVMなども作れるでしょう。ですから物理理論はエネルギーなどの領域を指定して、実験やその実験の結果を記述する物理理論を作るべきなのです。
付録Gの棒磁石モデルは低エネルギー領域では、二準位系量子力学の公理を満たす「量子系」として振る舞うと判断して問題ありません。下記記事にもあるように、棒磁石モデルの密度行列表示では、ボルン則も状態重ね合わせも出てきます。本書の付録Gでも強調しましたように、もちろん2つの棒磁石モデルではベル不等式が破れるので、それは四準位系の量子力学の公理を満たさず、その時点では理論として区別できるようになります。しかし1つの棒磁石に関しては、SG実験においてそれは公理系を満たす振る舞いをするため、それを量子力学的な対象、つまり限定された意味で、「量子系」と呼んでも問題は生じないのです。単なる言い回しの問題です。または、1つの粒子に対するシュレディンガー方程式をド・ブロイとボームの先導波理論でも表示できるように、「二準位量子力学の隠れた変数表示」と棒磁石モデルを呼んでも良いです。この棒磁石モデルも含めて、どんな理論でも様々なエネルギー領域での便利な表現の仕方や描像は変わるのです。
いいなと思ったら応援しよう!

