
Θ理論は、「堀田量子」第3章の反例ではない。
通称「堀田量子」と呼ばれる本書の読者のために、上のnote記事に書かれた中平氏の批判に対する回答を、こちらに書いておきます。なおこれまでの経緯は下記の私のnoteから辿れます。これまでも、そして今回も彼が続けている批判は、典型的な藁人形論法(strawman argument)に過ぎません。つまり堀田量子第3章はAという主張をしているのに、違う主張であるBを第3章はしていると彼は曲解をし、「そのBの反例を見つけた。だから堀田量子には致命的な誤りがある」と主張しているだけなのです。
最初の前提から説明します。物理理論では、どんな対象でも、それを測るどんな測定でも、エネルギーやその時点での技術などで決まる適用範囲があります。例えばスピン二準位系とみなされる銀原子や中性子のSG実験でも、それらの粒子の内部構造の励起が無視できる低エネルギーの実験です。(銀原子は原子核と47個の電子という内部構造をもち、中性子は3つのクォーク粒子とそれを繋ぐグルオン粒子という内部構造をもつ。)本書だけでなく、有名なJ.J.サクライなどの他の教科書でも、SG実験についてはこのことは大前提になっています。
SG実験におけるその実験領域では二準位ですが、もし粒子を測定するときに、高いエネルギーを粒子の内部構造に注入してしまう装置で物理操作を行うと、スピンの組み換えが内部で起こってしまいます。その励起状態のまま粒子をSG装置に通せば、多準位スピン状態が観測されます。低エネルギーの操作とSG実験だけならば二準位だったものが、例えば三準位などで記述される必要があります。
もしエネルギーがそれほど高くなく、SG装置を通過するころには増えた準位はもう見えなくなって、SG装置からは2つの粒子ビームしか出てこない場合もあり得ます。測定結果として2つの状態ですが、SG装置に入る前の中間エネルギー領域で、光子を出したり、別な測定器と接触をしていれば、その測定結果も使って、Θ理論などのなんらかの一般確率論の二準位版でその励起効果を解析できることも、もちろんあり得ます。これは最初の私の補足ノートの頃から本質的に何回も言っていることです。第2章と第3章では「理論の適用範囲を考えなさい」ということに過ぎず、これも当初から何回も中平氏に言っていることですが、Θ理論のような話は第15章でのテーマであり、彼が批判を続けている第2章と第3章での内容とは全く無関係なのです。あの手この手とわかりやすい説明へと変えはしましたが、私はずっと一環した主張を続けていることを、読者の方は本書や当初からの補足ノートからも辿れるかと思います。
多くの教科書でも、たとえば電子を「量子系」と呼ぶのが普通です。しかし将来の高エネルギー実験で、電子が量子力学の公理を満たさない振る舞いを観測する可能性もあります。でもそういう理論が作れるからと言って、「電子を量子系と呼ぶのは正しくない」と教科書には書きません。「電子が量子力学の公理を満たさない振る舞いを今後観測する可能性があるので、電子の系は量子系でない可能性がある」とわざわざ書く教科書も、これまでありません。
何故ならば、これまでの実験結果を集約して定義される波動関数や状態ベクトルは、次の量子力学の標準的な公理を満たしているからです。
公理1:量子状態は密度行列で表現される。
公理2:物理量はエルミート行列に対応する。
公理3:エルミート行列の固有値が、実験で観測される物理量の値である。
公理4:観測される物理量の値の確率はボルン則に従う。
公理5:密度行列の時間発展はシュレディンガー方程式で記述される。
この量子力学の公理をこれまでの実験データが満たしていることから「電子は量子系」と普通に言われているのです。高エネルギー領域でこの公理が成り立たない理論があっても、少なくとも現在のエネルギー領域では電子を「量子系」と呼ぶことに抵抗はないと思います。
また仮に量子力学の公理を満たさない振る舞いを高エネルギー領域で観測できたら、初めて「電子の系は量子系ではない」と言うことは可能となります。しかしこれまでのエネルギー領域のデータの1つの便利な「表記」としては、今後も密度行列や波動関数は使い続けられるでしょう。それは量子力学が出ても、古典領域の実験データは相変わらず、粒子の位置と運動量を基本として表記されるのと同じなのです。
また中平氏が提唱をするΘ理論の拡張では、「ボルン則」が成り立たないから、本書は間違っていると今回主張を加えられましたが、それも本書の主張を正しく理解されていないだけです。
なお念のため彼のΘ理論(もしくは今回少し拡張された理論)の枠組みで、本書での主張を正しく書くと次のようになります。
まず次の3つの3次元行列を定義します。
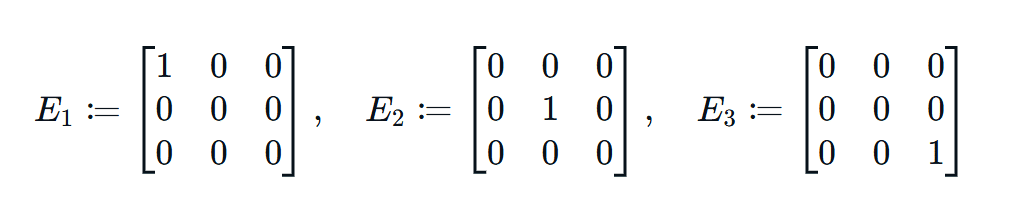
そして6次元行列のΘ理論での3つの状態に対する密度行列を下記で定義します。

この3つの状態は次のPOVM測定で同時識別可能です。

このPOVMはΘ理論のPOVM制限を満たし、そして3準位系の基準測定を成します。ここでΘ理論で許される他のPOVMとしては、上のPOVMを下記のように局所ユニタリ変換をしたものがあります。

これもΘ理論のPOVM制限を満たしています。この局所ユニタリー変換で生成されたPOVMの集合を、本書で扱われるSG実験のような「低エネルギー領域での測定」と、本書の文脈では定義をするのです。またこの実験を記述する理論での純粋状態は、E_1と任意の3次元ユニタリ行列を使って下記のように書ける密度行列ψとします。これもΘ理論で許されています。
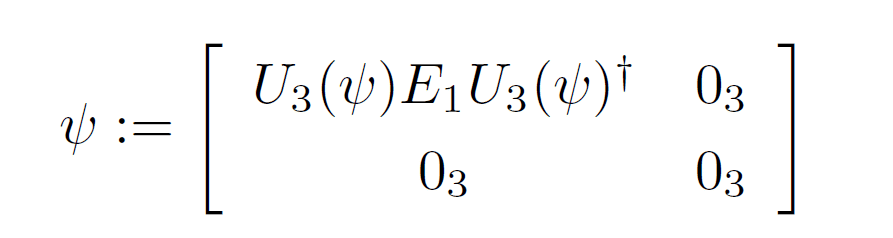
そして混合状態も含めた状態空間は、この純粋状態の確率混合で生成される下記の6次元密度行列全体と定義するのです。

本書第3章の意味での「三準位系」の状態空間は、Θ理論では、この(1)式の密度行列の集合で定義をされることに注意してください。これ以外のΘ理論の密度行列は、例えばスピン1粒子のシュテルン=ゲルラッハ(SG)実験などの、これまでの実験では観測されていません。第3章の文脈では、SG実験などの既存の実験データから構成される密度行列も(1)式で与えられているのです。
ここで3次元エルミート行列である8個のゲルマン行列に対応する物理量の測定を考えます。その各ゲルマン行列のスペクトル分解を、固有値と規格化された固有ベクトルとを使って、下記のように書きます。

この固有ベクトルと元の3次元基底ベクトルとの内積から作られる下記の3次元ユニタリ行列は、ゲルマン行列を対角化します。

その対角化により、固有値を対角成分にもつ対角行列が出てきます。

したがって元のゲルマン行列は、このユニタリ行列と対角行列により、以下で与えられます。

次にΘ理論でのこのゲルマン行列に対応する物理量の測定を、下記の6次元POVMで定義します。

これもΘ理論のPOVM制限を満たしています。そしてこの測定では、下記の確率分布が得られます。

そしてこの確率分布を使えば、ゲルマン行列に対応する物理量の期待値が、下記で計算可能となります。

そしてこの期待値から、今度はこの低エネルギー領域の実験を記述する3次元密度行列が、下記のように改めて定義可能となるのです。

この3次元密度行列はΘ理論でも非負ですし、定義に使用した期待値も下記の式で復元できています。

ですからΘ理論の中で考えられた(2)式の3次元密度行列が、「堀田量子」第3章での三準位系に対する密度行列になります。そしてこれが上で述べた量子力学の公理1に対応します。
次に公理2ですが、「堀田量子」第3章の物理量は、Θ理論の6次元空間の行列で、以下のように定義できます。つまり任意の実数値を各対角成分に持つ3次元対角行列を2つ用意し、その各行列に任意の3次元ユニタリ行列を使って、以下で定義される6次元エルミート行列です。

同じ物理量に対応する3次元空間での表現は、下記の任意の3次元エルミート行列になります。

Θ理論の中でも、このAは任意の3次元エルミート行列にできます。(3)式のAに対して、その右辺の現れたユニタリ行列を使って定義される、Θ理論で許された次の射影POVMを使えば、公理3は満たされていることがわかります。


この行列Aのスペクトル分解は

で与えられます。そしてこのm番目のAの固有値が観測されるΘ理論での確率は、

という3次元行列に対する「ボルン則」でも与えられることが示されます。これが公理4です。
またΘ理論でも、以下のような初期の純粋状態が純粋状態のまま時間発展をするダイナミクスは許されています。

この6次元密度行列に対応する純粋状態は、3次元密度行列でも純粋状態を記述しています。

また時刻tでの3次元状態ベクトルと、t=0の初期状態ベクトルを繋ぐ

の関係式を満たす時間依存したユニタリ行列も存在します。これから3次元ハミルトニアン行列を

で定義をすれば、そのハミルトニアンに対しての

というシュレディンガー方程式も成り立ちます。これが公理5です。
従ってΘ理論にも、5つの量子力学の公理系を満たす「堀田量子」第3章での三準位系はきちんと出てきており、この意味で中平氏の「Θ理論は致命的な誤りを示す反例」という主張は間違っていると言えます。
なお付録Gの隠れた変数理論の棒磁石モデルでも、SG実験のエネルギー領域では二準位で記述され、その実験データから第2章のように2次元密度行列が定義可能です。そしてボルン則や状態重ね合わせが出てきます。しかし棒磁石モデルに必要な謎の揺らぎをミクロに観察できる高エネルギー領域にいけば、二準位どころか、もっと多数の自由度、そしてそれを測定する装置や対応する測定のPOVMなども作れるでしょう。ですから物理理論はエネルギーなどの領域を指定して、実験やその実験の結果を記述する物理理論を作るべきなのです。その意味で、付録Gの棒磁石モデルも低エネルギー領域では二準位系量子力学の公理を満たす「量子系」として振る舞うと判断して問題ありません。下記記事にもあるように、棒磁石モデルの密度行列表示では、ボルン則も状態重ね合わせも出てきます。本書の付録Gでも強調しましたように、もちろん2つの棒磁石ではベル不等式が破れるので、それは四準位系の量子力学の公理を満たさず、その時点では理論として区別できるようになります。しかし1つの棒磁石に関しては、SG実験においてそれは5つの量子力学の公理系を満たす振る舞いをするため、そのような低エネルギー領域において「量子力学的な対象」、つまりこのように限定された意味で「量子系」と呼んでも問題は生じないとも言えます。単なる言い回しの問題です。または、1つの粒子に対するシュレディンガー方程式をド・ブロイ=ボームの先導波理論でも表示できるように、二準位量子力学の「隠れた変数解釈」または「隠れた変数表示」と棒磁石モデルを呼んでも良いです。この棒磁石モデルも含めて、どんな理論でも様々なエネルギー領域での便利な表現の仕方や描像は変わるのです。
いいなと思ったら応援しよう!

