量子力学の位置の期待値が古典的ニュートン方程式を満たすには。

古典力学のニュートン運動方程式は、粒子の位置座標に対する時間微分方程式ですが、時間の２階微分までしか出て来ない理由は、場の量子論の繰り込み理論を使わないと、ちゃんとしたは理解が得られないという意見があります。しかしこれは正しくはない観方だろうと、私は思っています。

場の量子論の繰り込み理論を考えます。出てくる低エネルギー領域の有効理論では、２階微分どころかいくらでも高階な時間微分項が出てきますが、その高階微分項の相互作用の強さを示す結合定数は、プランクエネルギーなどの場の理論の紫外発散切断（カットオフ）Λの逆数項の高次積の存在のために、非常に小さくなります。実質的に３階以上の高次微分項の相互作用は無視できるくらいに小さくなり、その結果として粒子の運動方程式には時間の高次微分項は出て来ないという主張です。

次に何故この主張が間違っているのかを見ていきましょう。非相対論的な低エネルギー領域で、量子的な粒子はシュレディンガー方程式を満たしますが、それは波動関数に対する時間に関しての1階の微分方程式です。また各物理量のハイゼンベルグ方程式にも、１階の時間微分しか現れません。ただし波動関数は各空間点に複素数を指定することで定まるため、空間体積分だけの無限個の自由度を持っています。古典力学では状態を決めるのに位置と運動量だけで済んでいたのですが（3次元空間ならば位置の３個、運動量の３個の合計６個の自由度）、量子力学では１つの粒子の自由度が無限個なのです。

これを反映して、位置などの物理量のハイゼンベルグ方程式を自由度に関した閉じた方程式にするためには、無限個の物理量のハイゼンベルグ演算子の連立微分方程式にする必要があります。それを粒子の位置座標などの特定の１つの自由度に関する１本の方程式にしようとすると、時間に関しては無限階微分まで入った方程式に成らざるを得ません。しかしこの理論にはそもそも紫外カットオフは必要とされず、その結果としてΛはこの方程式に出てきません。つまりその方程式に出てくる高階微分項は、繰り込み理論のときのようにカットオフΛの逆数で抑制されないため。一般には繰り込み理論のような1階や2階の時間微分しか出て来ない微分方程式に近似できません。

ここで、ハイゼンベルグ演算子はエーレンフェストの定理を満たすことを思い出しましょう。でもこれは位置の期待値が時間に関して2階の微分方程式を満たすことを保証しません。

それはポテンシャルV(x)の空間微分項の期待値が、その微分関数V'(x)に位置の期待値<x(t)>を代入したものと、一般には異なるからです。

エーレンフェストの方程式に出てくるポテンシャルの微分項の期待値は、一般には無限個の演算子の期待値の和で書けます。各項の係数は期待値の計算に使われる波動関数の詳細に非常に依ってきます。下のように位置の2乗の期待値も出てきますが、それは位置の期待値の2乗では書けません。

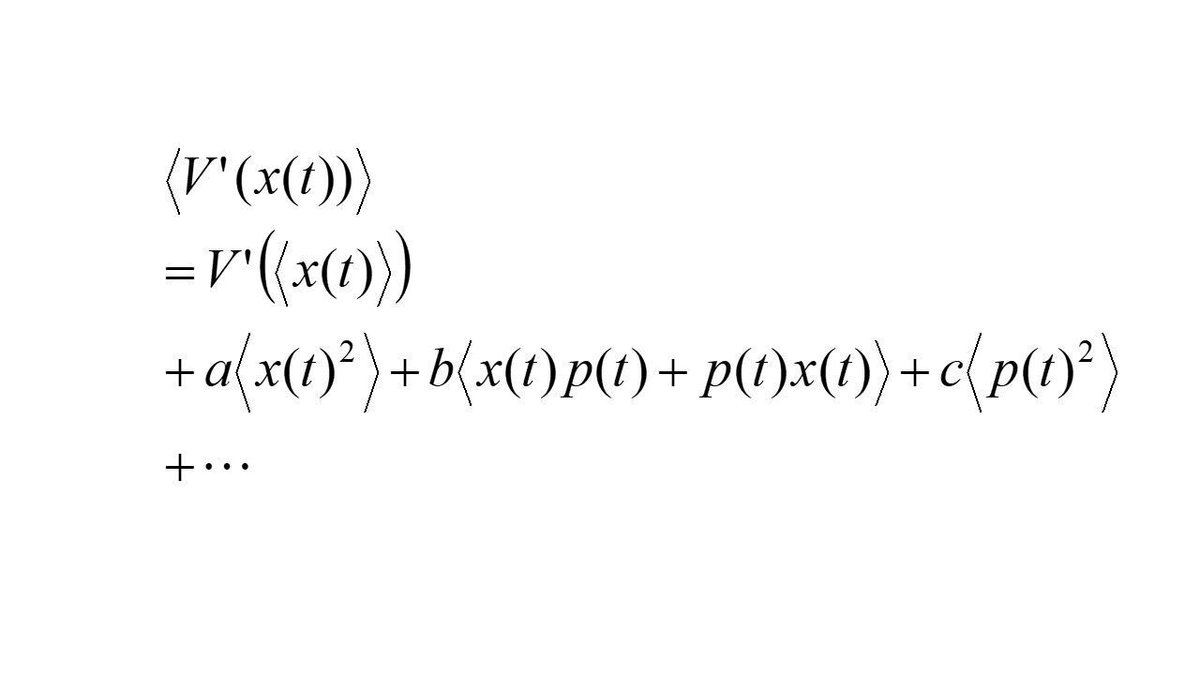
この独立した多数の演算子の期待値は、量子的な非可換性によって、位置のハイゼンベルグ演算子とは独立な時間発展をします。

つまり、量子力学では位置の期待値の運動方程式は閉じた時間の2階微分方程式では書けないのです。他の演算子の微分方程式と連立して解く必要あります。この他の方程式を使って、<x(t)>だけで閉じた方程式を書こうとすると、時間に関しての無限階微分方程式になります。

では、どのようなときに、その無限階微分方程式が古典的なニュートン方程式になるかというと、考えている量子状態がマクロな古典的状態を記述する場合に限ることがわかります。つまり波動関数（量子状態）次第です。

一般の量子状態を初期状態にすると、時間に関して2階微分方程式であるニュートン方程式は出てきません。従ってニュートン方程式が出てくる条件は、場の量子論の繰り込みと全く関係がありません。