
時間反転で電場の符号は反転せず、磁場の符号は反転するのは、相対論と整合しないのか?
時間反転で電場は符号を変えないが、磁場は符号が変わると習ったことはありませんか?でも、相対論を知っていると、一見これは変だと感じます。電場と磁場は、4次元電磁ポテンシャルから導かれる反対称テンソルであり、時間反転ではその電場の符号は変わるが、磁場の符号は反転しません。このギャップはどのように理解できるのでしょうか?それを今回説明します。
物理学理論の基礎方程式の多くは、時間反転対称性を持っています。
電磁気学のマクスウェル方程式も、その時間反転対称性をもつ運動方程式の1つです。
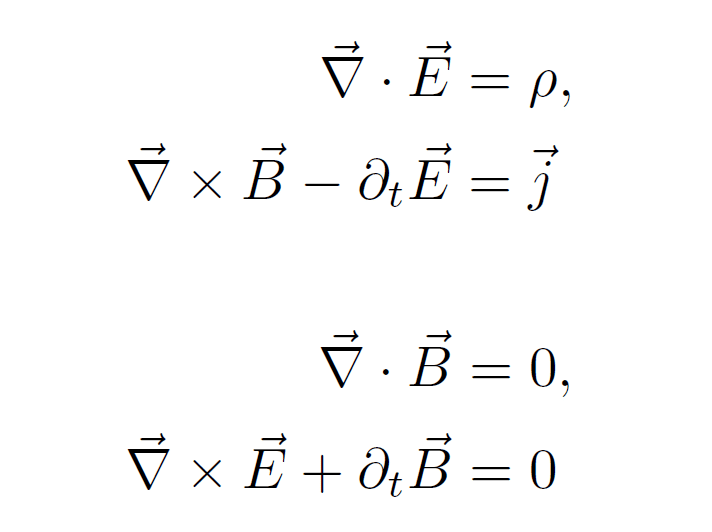
この右辺に出てくる電荷密度と電流密度を、電荷qをもつ粒子の場合に書けば、次のようになっています。

ここで大文字のXベクトルは時刻tでの、この荷電粒子の位置を表しています。そしてこの荷電粒子の位置は

という方程式で、その運動が決まっています。
ここで図1のように、電場で減速されている電子を考えてみましょう。図の左側から速いスピードでやってきた電子が、正方向の電場によって減速された後、遅くなって右側領域に出てきます。電場の力は電荷×電場で与えられますが、電荷はq=-eという負の値をとり、電場は今の場合は正です。図1で電場が電子に与える力Fはx軸の負方向に向いており、そのため電子は減速をしているのです。

さて、図1の状況で時間反転を考えてみましょう。図2のように、時間反転は、時間の流れを映画フィルムの逆回しのようにひっくり返します。

ですから時間反転した図2では、電子は右から左へと運動をしており、最初右側では小さかった速度が、電場の力によって加速をして、左側では大きくなります。つまり電場が電子に与える力F'の向きは、この場合は元の図1のFと同じ、x軸負方向のままです。電子の電荷q=-eは変化しないと思えば、電場Eの向きは時間反転で反転しません。
では磁場の時間反転はどうでしょうか?図3のように、z軸正方向にかけた一定磁場中を円運動する電子を考えてみます。この場合は上から見て反時計回りに電子は回転しています。磁場で支えられているこの円運動は、円の中心に向かう力Fによって起きています。その力Fのベクトルは、粒子の速度ベクトルと磁場ベクトルとの外積に、粒子の電荷を掛けたものに等しいです。

この図3の時間反転が、図4です。

電子の円運動の向きは逆転をして、時計回りになります。またその速度ベクトルも時間の反転に従って符号が反転します。それでも円の中心に向かう磁場の力F’を維持するために、磁場の向きを反転させる必要があります。つまり時間反転で、磁場の符号はひっくり返るのです。まとめると、時間反転では(1)式のように電場は反転せず、磁場は反転するのです。

ここまでは、物性物理などでも用いられる話です。しかし荷電粒子と電磁場の相対論的な量子効果を扱う量子電磁力学(quantum electromagnetic dynamics, QED)では、電場と磁場の時間反転操作の定義は、(1)式とは異なります。
まず電場と磁場は、4つの成分をもつ電磁ポテンシャルを使って、

と書けます。この電磁ポテンシャルの4成分を、相対論ではまとめて1本の4次元ベクトル場Aとして扱い、また電場と磁場もまとめて、下記のように定義をされる反対称テンソル場fで書かれます。

このAは座標変換の下でも、相対論的なベクトルとして変換をされるものです。ローレンツ変換だけでなく、(4)式のように、時間反転の変換でもそれは同様です。

このAの時間反転で得られる電場と磁場の変換は、
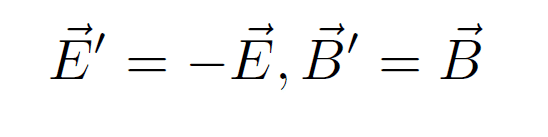
となり、上の(1)式の時間反転の変換とは符号が異なっています。しかし、QEDのような相対論的な場の量子論では、この(5)式のように時間反転を再定義したほうが、都合がよいのです。
たとえば図5のようなファインマングラフの過程を考えてみましょう。図の下側が過去で、上側が未来になっています。横方向は空間自由度です。この時空の中を、最初電子は過去から未来へと進み、電磁場Aと相互作用をした後に今度は未来から過去へと伝搬します。そこで再び電磁場Aと散乱して、過去から未来へと向きを変えます。この理論では、このように電子は時空中の過去と未来を行ったり来たりできるのです。
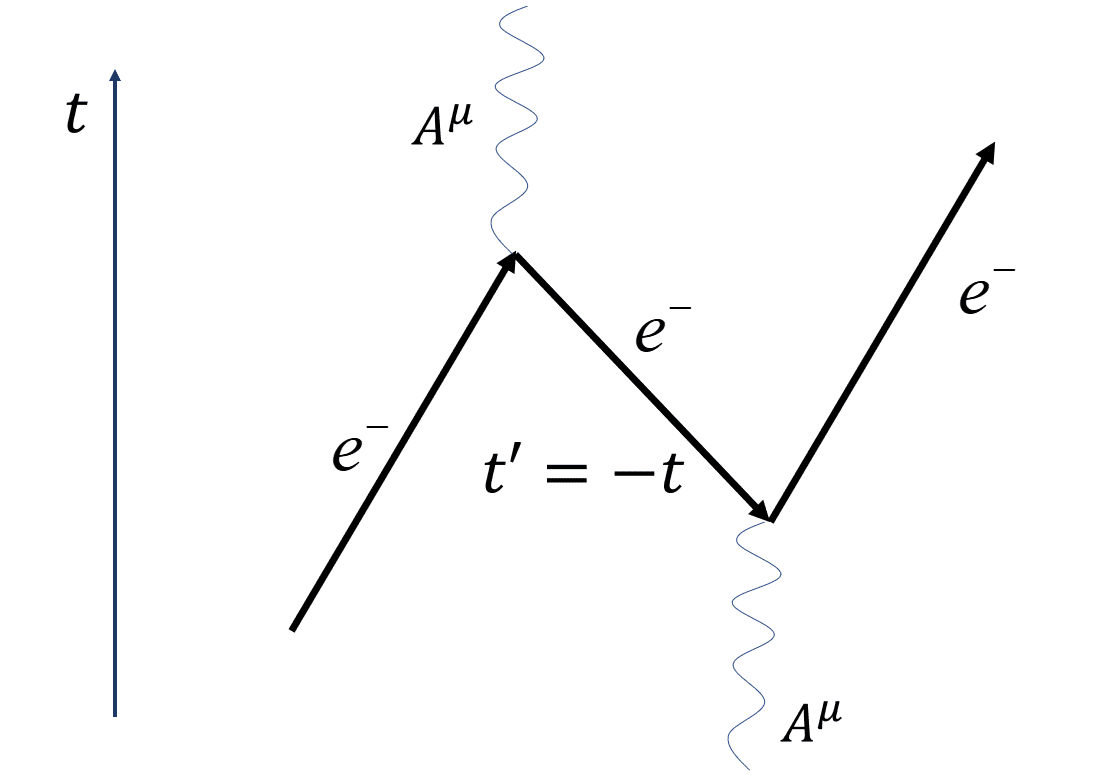
しかし「時間逆行をする電子」とは直観的にわかりにくいですね。それは、図6のように、その電子を時間反転させて、過去から未来に進む電子の反粒子、つまり「陽電子」であると解釈するのです。

図5のファインマングラフと図6のファインマングラフは、物理的には同じ過程を表しています。過去には電磁場Aと1番目の電子があり、そのAから新たに2番目の電子と陽電子が対生成をしています。その陽電子は時間の正方向に進んで、元々あった1番目の電子と対消滅をして、電磁場Aに戻ります。したがって未来には陽電子は居なくなり、そのAと2番目の電子だけが残っています。このように時間逆行をする電子を時間順行する陽電子と解釈することは、計算の見通しを簡単にしてくれるメリットがあるのです。同様に時間逆行する陽電子は、時間順行する普通の電子であると、相対論的な場の量子論では解釈するのです。
実際この時間反転の定義は、(6)式のQEDのラグランジアンや、そのディラック場の運動方程式でも確かめられます。

このラグランジアンから得られる電荷qのディラック場の運動方程式は

です。物性分野で考える非相対論的な電子場とは異なり、この相対論的なディラック場には電子と陽電子の2つの自由度が既に組み込まれています。つまり電荷が-eと+eとなる2種類の粒子が、自動的に含まれていることが重要な点です。なので物性物理とは異なり、時間逆行をする電子を、時間順行する陽電子と考える余地があるわけです。
ここでガンマ行列をディラック表示で与えると、

となっています。そしてQEDにおいて、この表記での時間反転は

で与えられています。この変換を(7)式の運動方程式に対して行うと、
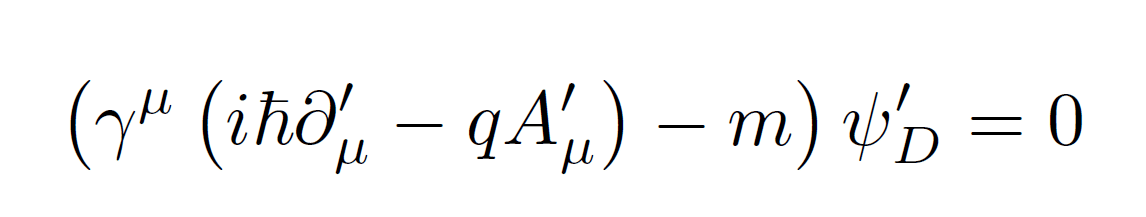
という方程式になりますが、ここで重要なのは、(7)式と比べて

と、電荷の符号が確かに反転をしている点です。つまりこの意味では、QEDの時間反転によって、同時に電荷も反転するのです。
(註:QEDには時間反転とは独立に電子と陽電子を入れ替える、荷電共役という変換も定義されています、これは運動の時間の向きはそのままにして、電子と陽電子を入れ替えています。ディラック表示では、

と荷電共役変換は書かれます。この式の中で、時間は反転をしていません。)
では(5)式での相対論的な時間反転の再定義で、図1の過程の時間反転を見直してみましょう。

図7のように、今回は電場の符号が反転をしますが、同時に粒子が電子から陽電子に化けています。ですから、力F自体は電荷と電場の符号の2回の反転のために変化しません。図7の陽電子は右から左へと運動し、そして反転した電場によって、その陽電子が加速をされるのは、図2の時間反転電子と同じです。
また図3の磁場の時間反転は、図8のようになります。

相対論的な時間反転では、磁場の向きは変わりません。しかし電子が陽電子になり、そしてその運動の速度ベクトルの符号も時間反転でひっくり返ります。磁場は変わらず、そして電荷と速度の符号も同時に反転するので、得られる力F’は図3と同じ中心力のままです。その結果、図4の電子と同じように、陽電子が時計回りの円運動をします。
このように、電場と磁場の物性物理における時間反転の定義と、相対論的な場の量子論での時間反転の定義は、異なります。相対論では、時間反転を含めた電磁ポテンシャルAの座標変換則を、飽くまで相対論的なベクトルの変換則に一致させたほうが、ファインマングラフでの計算とは相性が良いのです。ただしこれは1つのディラック場に対等に含まれている「電子」や「陽電子」などの自由度に対する粒子の名前の付け方の記法に過ぎません。
一度きちんと時間反転の定義を決めて、一貫した計算をするのならば、(1)式の定義でも(5)式の定義でも良いのです。どちらの定義でも時間反転の物理現象には違いは起きません。相対論的な場の量子論での記法では、電磁ポテンシャルの時間反転は下記の変換になります。

そしてこのAと電荷qの積の時間反転は下記になります。
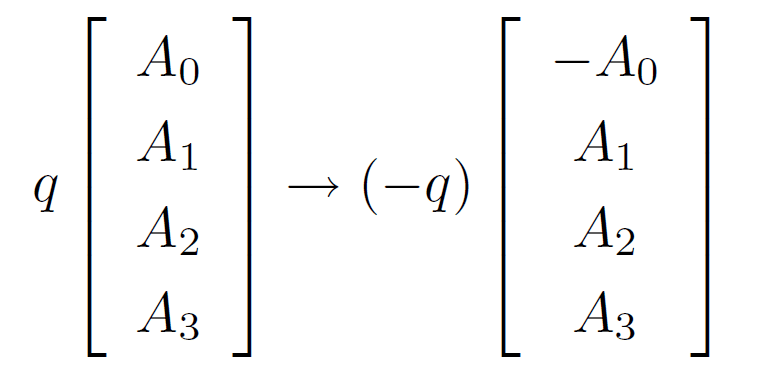
これから得られる電荷×電場と電荷×磁場の時間反転のルールは

で与えられることになります。これが場や粒子に与える相互作用や力を決めています。一方で、物性物理でよく採用される、電磁ポテンシャルの時間反転は符号が異なり、

で与えられています。しかし電荷×Aの符号については、相対論的な場の量子論の場合と一致します。

したがって、物性物理での電荷×電場と電荷×磁場の時間反転のルールは、下記のように、相対論的な場の量子論でのルールと一致します。ですから相互作用や力について、どちらの時間反転を採用しても、その物理に違いは生みません。

いいなと思ったら応援しよう!

