
「ハミルトニアン」は、物理学では特別なのか?
解析力学では、古典的な物体を扱う際にハミルトニアン (Hamiltonian) という物理量が登場します。通常、英語の頭文字を取ってHと記されることが多いです。このハミルトニアンは、物体の運動を記述する正準方程式に現れます。

特定の初期条件を与え、未来の挙動を予測する場合、この正準方程式を解くことが重要です。そのため、ダイナミクスを支配するハミルトニアンHは、一見すると特別な地位を持つ物理量のように思えます。確かにHは非常に便利な量ですが、「Hは物理量として特別か?」と改めて問うと、実はそうでもないのです。
ハミルトニアンHは物理変数pやqに依存します。しかし、Hがpとqの関数として時間tに依存しない場合、正準方程式の解に対してHの値(エネルギー)Eは時間に依存しなくなります。これが、いわゆるエネルギー保存則です。
エネルギー保存則は、物理学の学習において度々出てくる重要な概念ではあります。ただし、保存される物理量はエネルギーだけではありません。例えば、対称性を回転させても正準方程式が保たれる場合、角運動量が保存されます。また位置座標を一定量ずらす(空間推進変換)場合に正準方程式が保たれるなら、運動量が保存されます。このように、エネルギー保存則だけが特別なわけではなく、他の物理量にも対応する保存則が存在します。
解析力学では、ある一般的な変換の下で正準方程式が不変となる対称性が存在する場合、その対称性に対応した物理量の保存則が成立することが示されます。数学的には、この変換の生成子と呼ばれる特定の物理量が時間変化しないことが分かります。エネルギー保存則は、そのような保存則の一例にすぎません。
例えば、時刻の基準点をずらす変換は時間推進変換と呼ばれます。この時間推進変換の下で正準方程式が不変である場合、その系は時間推進対称性を持つと表現されます。そして、この時間推進対称性を持つ系では、時間推進変換の生成子であるハミルトニアンHが保存されます。
ここで強調されるべきこととして、次の点があります。具体的に1つの系を考えた場合でも、時間推進変換の生成子であるハミルトニアンは1つに決まるわけではありません。時間の流れ方を物理変数(p,q)の初期条件に応じて変更することで、異なる時間座標を定義することができるためです。その結果、各時間座標に対応する異なるハミルトニアンが定義されます。仮に元の時間座標でのハミルトニアンをHとするならば、新しい時間座標に対応するハミルトニアンは、任意の単調増加関数F(x)を用いてF(H)と表すことができます。詳しくは、以下の記事をご参照ください。
生成子として多くのハミルトニアンが存在することは、実はハミルトニアンに特有の性質ではありません。他の変換を生じさせる生成子である物理量Aについても、同様に多くの異なる生成子F(A)を定義することが可能です。これについて、以下で見ていきましょう。
まず(p,q)の関数としてみたときに時間依存性をもたない一般の物理量Aを考えます。

任意の初期値(p(0),q(0))に対して、パラメータbに依存した下記の変換をしてみましょう。

ここでbは実数であり、連続的に変化させられるとします。そしてこの変換は、Aに対しての下記の方程式を満たすように定義します。

このときbはAに対する正準共役な量とも、解析力学では呼ばれます。そして(3)式を満たすとき、Aはbの値に依らないことがわかります。

ここでbは時間である必要性はないのですが、(4)式はbの変化に対するAの保存則と見なせます。
ここで単調増加関数F(x)を使ってF(A)という物理量を作ってみましょう。Aはbの変化に対して保存しますので、下記の関係も成り立ちます。

ここで相空間の各点(p,q)において新しいパラメータβを下記の式を使って導入します。

上式右辺に出てきたN(a)という関数は、仮にbを時間座標と見なしたときのラプス関数のことです。

このN(A)もbの変化に対して不変です。後は上のnote記事でハミルトニアンHに施した同じ計算で、下記の関係が得られます。

つまり新しいパラメータβをずらす変換は、F(A)を生成子とする正準変換であることが示されるのです。以下でそれを確かめてみます。
まず(5)式は

と変形されます。更にラプス関数Nのbの変化に対する保存則を使うと、変換前の(p(0),q(0))の値だけで決まるA(p(0),q(0))=aの値を使って、
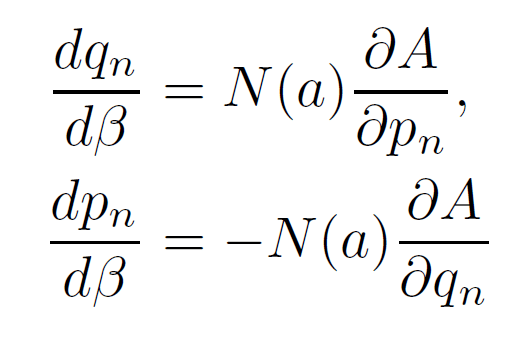
とも書けます。そしてこの両辺をN(a)で割った後に

というbとβの関係を使えば、元の(3)式のAによる正準変換が確かに出てきます。
したがって、ハミルトニアンHだけでなく、任意の物理量Aについても、相空間の各点ごとに異なるパラメータbの値を選ぶことで、F(A)という生成子とその変換を考えることができます。この意味でも、ハミルトニアンHは特別な物理量とは言えません。
これからの時代には、量子コンピュータなどのマクロな量子制御系の実現が期待されています。それに伴い、ハミルトニアンも自由にデザインできるようになるでしょう。その結果、任意に選んだ物理量が短い離散的な時間ごとに保存されるような時間発展を構築することも可能になります。
量子力学を前世紀のように正準量子化から学ぶと、ハミルトニアンHが運動エネルギーKとポテンシャルエネルギーUの和として書かれることに、深い意味があるように思えるかもしれません。しかし、現代的な量子力学の理解では、ハミルトニアンHの形は固定されたものではなく、「自由にデザインされるもの」という認識が大切になります。
いいなと思ったら応援しよう!

