測定後状態は固有状態になるが、確率分布は正確にならない量子測定は存在しない。

拙書『入門 現代の量子力学』でも解説しましたが、量子力学の測定は、学部で習う「射影測定」に限りません。

射影測定、つまり理想測定以外にも、多様な量子測定が知られています。
そして例外を除いた多くの実験では、理想測定は実現をしていません。（なおスピン粒子のシュテルン＝ゲルラッハ実験は理想測定の例です。）

理想測定では、１つ目の特徴として、(1) 観測される物理量の値の確率分布が、固有ベクトルの射影演算子を使ったボルン則で与えられます。例えば純粋状態では、その状態ベクトルと測定をする物理量の固有ベクトルの内積の絶対値の２乗で、その観測確率は与えられます。２つ目の特徴として、(2) 測定後の対象系の状態は、物理量の行列または演算子の固有値に対応する固有状態となります。

「正確な測定」と呼ばれる実験では、(1)は満たされているのですが、(2)が一般には破れています。(2)も満たす正確な測定が理想測定です。物理量の確率分布は理想測定と同じ結果なのですが、測定後状態が物理量の固有値の固有状態に正確には一致せずにずれる場合が、理想測定ではない正確な測定となります。この場合は同じ測定を２回繰り返しても、最初の物理量の値とは異なる値が２回目に出たりします。

それ以外にも(1)と(2)の両方が必ずしも実現をしない「一般測定」というクラスの測定もあります。そして普通の実験では、理想測定でも正確な測定でもない、一般測定の場合が多いのです。

これらの量子測定の数学的定式化は測定演算子M(m)というものを使って成されます。詳しくは『入門 現代の量子力学』をご参照ください。対象系の測定前の状態を表す密度行列ρと測定演算子を使うと、物理量の値mが観測される確率は下記の(1)式で与えられます。

(1)式

またmという値を得たときの測定後状態は、同じく測定演算子を用いた下記の(2)式で計算されます。

(2)式

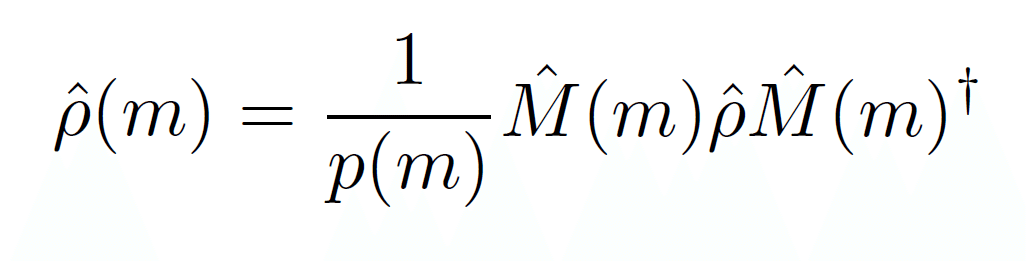
この測定理論は、小澤正直らによって数学的に整備をされました。まとめると、量子測定は図１のように分類をされます。

図１

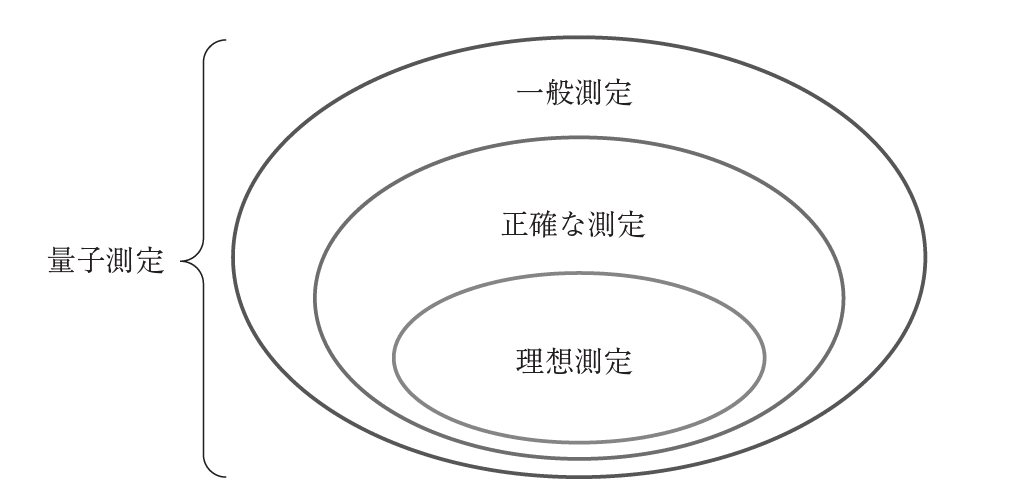
ここで測定後状態が固有状態であるという条件は満たすが、観測確率が理想測定の結果とは異なる量子測定はないのか？という疑問を思われる方もいるかもしれません。しかし量子測定理論を使うと、そのような測定は存在しないことも分かります。

もし測定後状態が固有状態であるとすると、(2)式から測定演算子は固有状態への射影演算子であることが分かります。そして(2)式の両辺でトレースをとると、(1)式が自動的に得られますが、それはその射影演算子を使った理想測定でのボルン則と同じです。つまり測定後状態が固有状態であると仮定すると、自動的にそれは理想測定になるのです。測定後状態が固有状態ならば、２回同じ測定をしても、必ず同じ物理量の値が出てくるので、それはまさしく理想測定にしか成りません。ですので図１の量子測定の分類は正しいことが分かります。