
調和振動子は自由粒子に変換できる:双対性の考え方
理論物理学において、対称性は重要な概念です。系に時間座標の推進対称性があれば、ネーターの定理から重要なエネルギー保存則が出てきますし、空間座標の推進対称性があれば、運動量保存則も導かれます。一方で、対称性とは異なる「双対性」という概念もあります。物理系の自由度を別な自由度に置き換えたり、また一般相対論で行うように時空の座標系を曲がった座標系に書き換えたりすることで、ひとつの物理系のダイナミクスが他の物理系のダイナミクスとなる場合があります。このとき、その2つの物理系の間には双対性があると呼ばれます。対称性は、この双対性で繋がる2つの系がたまたま同じ1つの系である場合に対応します。この双対性の非自明な例として、負の宇宙項を持った量子重力理論と時空次元が1つ小さな平坦時空における量子物質の共形場理論が等価であるという、AdS/CFT対応なども知られています。
今回はそのような双対性の簡単な最も簡単な例として、調和振動子と自由粒子の間の双対性である「高木変換」を紹介してみようと思います。(文献は下記の論文[1]です。)
まず1次元空間を運動する単位質量の自由粒子の作用を、下記のように書きます。

ここでは粒子の位置座標がQで、時間座標をτとしています。次にωを正の定数として、時間座標をτから下記のように別な時間座標tへと書き換えます。
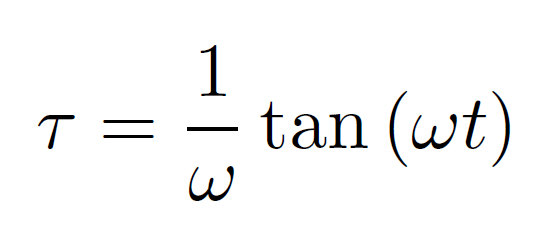
同時に粒子の位置座標をQから別なqへと、下記のように書き換えてみます。

ダイナミクスに影響を与えない作用の境界項を無視すれば、この2つの変換を行うことで、Sは下記のような角振動数ωの調和振動子の作用に化けます。

ここで(1)式からわかるように、調和振動子の振動の半周期の運動が時間的に引き延ばされて無限の過去から無限の未来に写像され、また有限空間領域内部で変化をしていた調和振動子のq(t)は、(2)式によって実数直線上のマイナス無限大からプラス無限大へと(またはその逆の)等速運動をするQ(τ)へと写像されます。従って、このそれぞれの時間領域において、確かに自由粒子と調和振動子の間には双対性があると言えます。
上では角振動数ωの調和振動子と、ω=0としての自由粒子の間の双対性を確認したわけですが、一旦この関係に気づいてしまうと、角振動数ωの調和振動子と別な角振動数Ωの調和振動子の間の双対性の関係も自動的に導けます。一旦角振動数ωの調和振動子系を(1)式と(2)式の変換によって自由粒子系に移した後、再びωをΩにした(1)式と(2)式の逆変換を自由粒子系に施して、角振動数Ωの調和振動子系に移せばよいのです。
具体的には時間tと位置座標qを、下記の式で時間t'と位置座標q'に変換します。


すると確かに変換後には、作用Sが下記のようになって双対性が確認できます。

異なる角振動数の調和振動子同士の間にも、このような双対性の関係があるのです。
双対性が一旦見つかると、片方の物理系における対称性を他方の物理系のダイナミカルな対称性として輸出することもできるようになります。以下では自由粒子系の対称性を、調和振動子系へ輸出することを考えてみます。
なおこれまではラグランジュ形式で説明をしましたが、もちろんハミルトン形式でも全く同じです。ハミルトン形式で見てみましょう。自由粒子の正準共役運動量は下記で与えられます。

そして単位質量の自由粒子系のハミルトニアンは下記で与えられます。

このハミルトン形式での運動方程式は、下記の正準方程式です。
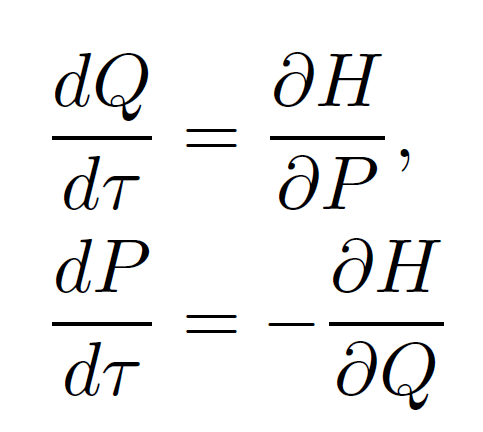
この正準方程式からは、ラグランジュ形式でのオイラー方程式と同じ、下記の自由粒子の運動方程式が得られます。

この方程式の一般解は

です。ここで右辺に現れている定数は、それぞれτ=0における初期位置と初期運動量となります。

これは自由粒子系ですので、例えばvを定数とした以下のガリレイ変換における対称性の存在が知られています。

実際に(6)式の一般解においてこのガリレイ変換を行うと、その答えは次のようになります。

ガリレイ変換はこの自由粒子系の対称性ですから、もちろん変換後も(5)式と同じ運動方程式を(7)式の時間の関数は満たしています。
上のような対称性の議論では、1つの変換で異なる時間座標や位置座標を繋ぎますが、このことは見方を変えると、一般解での初期条件を下記のように変えただけだとも分かります。

このような見方は、ガリレイ変換に限らずに一般の変換にもできます。(6)式の一般解において、初期条件を下記のように一般的に変換してみましょう。

この変換後の(6)式の一般解は

となりますが、初期条件を変えただけなので、もちろんこれも全く同じ下記の運動方程式を満たします。

もし(8)式の初期条件の変換を正準変換にしたいのならば、

という条件を、(8)式の変換関数に課せばOKです。
ここで時間反転をさせて時刻τの位置と運動量を、時刻τ=0の位置と運動量へと移す下記の変換は、正準変換だったことを思いましょう。

そして時刻τ=0における(8)式の変換を行います。

その変換の後、時刻τ=0から時刻τまで時間発展をさせる下記の変換も正準変換です。

この3つの変換の合成から

という、自由粒子の解を別な解へと写像する一般変換が作れます。ここで(9)式が正準変換に限定をされていれば、合成された(10)式の変換も正準変換です。そして上の議論から、この(10)式の正準変換では、ハミルトニアンHも、その形は変わりません。ですから正準形式での最も一般的な対称性を、(10)式は与えていることが分かります。
自由粒子系のガリレイ対称性や(10)式の一般対称性は、(1)式と(2)式の変換によって、角振動数ωの調和振動子系のダイナミカルな対称性として輸出することもできます。調和振動子系をまず自由粒子系に写像をして、そこでガリレイ変換をした後に、再び元の調和振動子系に戻せばよいのです。これで得られる調和振動子系での対称性変換も、元々あったその調和振動子側の一般解において、その初期条件を変化させるだけのものになっています。また正準方程式で記述される任意のハミルトン系において、時刻τ=0における全ての正準変換を元とする正準変換群は、ダイナミカルな対称性として実現するのです。性質がよく知られている回転変換群や共形変換群だけに注目をして解析を進めることも応用上では多いのですが、ダイナミカルな対称性としてはそれらの変換群が特別なわけではなく、全ての正準変換は同等にダイナミカルな対称性の変換とみなせるのです。
なお今回は古典力学で双対性を扱いましたが、自由粒子と調和振動子の双対性は、そのまま量子力学でも成り立つことが知られています。(これについては論文[1]を参照。)拙書『入門現代の量子力学』第10章では、2次元調和振動子と一様磁場中の荷電粒子の双対性の量子版が出てきます。
また簡単のために自由粒子と調和振動子の例を挙げましたが、双対性があれば、或る物理系Aの対称性から、双対性で移れる別な物理系Bの対称性を構成することも、少なくとも古典力学ではいつでも可能です。まずAのハミルトニアンで時刻τから時刻τ=0に時間を戻します。次に時刻τ=0において、位置と運動量の初期値に対して(9)式の一般的な正準変換を施します。その後で、今度はその新しい初期値から出発して、Bのハミルトニアンで時刻τまで時間を進めるのです。この3つの正準変換の合成で得られる変換は、AとBを繋ぐ双対性の変換とみなせるのです。
このような形で双対性と対称性を組み合わせることで、より複雑な物理系のダイナミクスを捉えることは、現在でも理論物理学の様々な分野で頻繁に行われているのです。
[1] Shin Takagi, Progress of Theoretical Physics, Vol 85, No 4, 723 (1991).
いいなと思ったら応援しよう!

