
樽のサイズによるお酒の熟成の差異について
こんにちは、さてぃです。
今回は樽の大きさにおける熟成速度の違いについて思った事を書き記していこうかと思います。
巷では、樽の大きさが小さいほど熟成が早いみたいな事がよく言われます。これがどんな仕組みでそうなっているのかを改めて基礎的なところから考察し、本当に任意のタイミングで樽の小ささによる優位性がちゃんと担保されるのかを論じていこうと思います。
イントロダクション
まず樽の大きさが小さいほど熟成が早いというのはどんな仕組みなのかを解説していきたいと思います。
結論から言ってしまえば、樽自体が小さくなるほど中の液体の容量に対する熟成する面の比率が大きくなるからです。
これだけだとよく分かりづらいと思うので、そもそも熟成は樽のどの箇所で進行するのかを考えた後、実際に簡単な計算をしてみます。
熟成はどこで進行するのか?
ウイスキーやワインを少し嗜んでいる方はご存知の方が多いと思いますが、熟成は樽と触れている部分(下記の図の赤い部分)で進行します。
つまり、熟成の進行度は樽の表面積に比例するという事です。これだけ覚えて、次の議論に進みましょう。

樽の大きさによる熟成の進行度合い
話を簡単にするため、樽を一辺の長さが$${L}$$の立方体に見立てて、中にお酒が全て入っているとします。

1つの面の面積は$${ L^2}$$になるので、表面積は
$$
6\times L^2=6L^2
$$
となり、これが先述の通り熟成される箇所のパラメータとなります。
一方で体積は$${L^3}$$と書けるので、体積に対する表面積の割合(=表面積/体積)は下記のように書く事ができます。
$$
\frac{6L^2}{L^3}=\frac{6}{L}\propto \frac{1}{L} (1)
$$
これが先述のとおり熟成の進行度合いになります。熟成度合いは立方体の大きさ$${L}$$の逆数に比例するので立方体が小さければ小さい程熟成は早く、大きければ大きいほど熟成は緩やかになるという事です。
巷で言われる、小さい樽ほど熟成が早く進むというのはこの事を表現しています。
これは生物学や工学で用いられる2乗3乗の法則と呼ばれる法則の1例と見なせるため、以後2乗3乗の法則と呼ぶことにします。
ちなみに、寒冷な地域ほど動物の体が大きくなるというベルクマンの法則も同様に2乗3乗の法則の考えで説明することができます。つまり、寒さから体を守るためには、体積(=体全体)に対する表面積(=外気と触れる皮膚)の割合を小さくするため、動物は体を大きくする必要があるというわけです。
要は$${L}$$を大きくすれば冷えにくい体になるので、寒冷な地域の動物の体は大きくなる傾向があるという事です。
2乗3乗の法則の樽内熟成への適用に対するアンチテーゼ
樽が小さいほど熟成が早くなるという通説への理解が進んだところで、果たして本当に中に入っているお酒の熟成は任意のタイミングで樽が小さいほど早くなっているのでしょうか??
実際の液体の熟成と今回仮定したモデルの違いは下記になります。
エンジェルズシェアを考慮していない
実際お酒などの熟成はエンジェルズシェアが起きるため、今回仮定した液体が全て入っている状況と異なる
樽は立方体ではない
樽の実物は立方体ではなく、円柱に近い形をしている
後述しますが、後者の影響はおおざっぱなエッセンスをつかむだけなら考慮しなくて良いため、前者の状況をまず考えていきましょう。
エンジェルズシェアを考慮した場合の熟成の進行度合いの変化
いきなり計算!!する前にエンジェルズシェアがかなり進んだ場合の漸近的な振る舞いを考えましょう。
限界までエンジェルズシェアが進んだ時には図のような状況になると思います。

明らかに体積に対する表面積の割合って増えてませんかね??
ちょっと計算してみましょう。
液面の高さを$${h<< L}$$とすると、接地(表)面積は、
$$
L^2 + 4\times Lh = L(L+4h)
$$
となります。また、体積も同様に計算すると
$$
L^2\times h = L^2h
$$
となるので体積に対する表面積の割合(=表面積/体積)は
$$
\frac{L(L+4h)}{L^2h }=\frac{1}{h} + \frac{4}{L} (2)
$$
となります。この値は明らかに$${h}$$が小さければ小さいほど(エンジェルズシェアが進むほど)大きくなっていきます。
$${h}$$が小さくなるほど$${L}$$のみが含まれる2項目の影響は少なくなり、したがって熟成における樽の大きさの差異は少なくなることが分かります。
直感的に考えた結果と一致しますね!
中身が全て入っている時からエンジェルズシェアが進んだ時の振る舞い
(1)式で全て中身が入っている時からどんな具合で熟成が進んでいくかをもう少し詳しく見てみます。
$${h\leqq L}$$なので、(2)より表面積の割合の最大値は
$$
\frac{1}{h} + \frac{4}{L} =\frac{1}{L} + \frac{4}{L}= \frac{5}{L} (3)
$$
となります。(1)の値より$${1/L}$$だけ小さいのは上面の熟成を考慮していないからです。ちょっと減ったくらいじゃむしろ熟成の勢いはいっぱいの時よりも落ちてそうですね。
仮に、$${h=2L/3}$$(半分より液体が入っている状態)としてみると同様に表面積の体積に対する割合は$${11/2L}$$となり、フルで入っている状態よりも小さい値になっています。(ただ、(3)の値よりは増えているのに注意)
同様に樽の半分まで液体が入っている状態$${h=L/2}$$を考えると表面積/体積の値は$${6/L}$$となり、満タンの状態と熟成の進行度合いは一致します。以降、$${h}$$をさらに小さくするほど、満タンの状態よりも熟成の進行は早くなることがわかると思います。
振る舞いをまとめると、満タンの状態から液体の量が半分になるまでは熟成の進行速度は落ちていきますが、半分を切ってさらに減っていく時は熟成は満タンの時よりも早く進行し、樽自体の大きさの影響も少なくなっていくという結果になります。
実際の樽に近い形状で再度計算してみる
前述の通り、実際熟成に使用されるのは樽なので立方体とは異なります。
ただし、樽の形状を正確に計算していくとなると解析的に計算するのはかなりきついので、円柱として近似します。それでもなかなかめんどい計算になるので、スキップしてもらって大丈夫です。(ガチ勢向け)
円柱の場合、高さを$${l}$$として、半径を$${r}$$とするとフルで液体が入っている時の体積は

$$
\pi r^2 \times l = \pi r^2l
$$
となります。
一方で表面積は
$$
2\pi r^2 + 2\pi rl= 2\pi r(r+l)
$$
となるので、熟成の進行度(=表面積/体積)は
$$
\frac{2\pi r(r+l)}{ \pi r^2l}=\frac{2(r+l)}{rl}=\frac{2}{l}+\frac{2}{r} (4)
$$
です。パラメータこそ異なりますが、$${r}$$や$${l}$$を小さくする(=樽を小さくする)とこの値は大きくなります。
つまり、ここでも入れ物の大きさを小さくすることで熟成の進行が早くなる事がわかります。
エンジェルズシェアで液体が減った場合も考えてみます。
断面を下記の図とすると、空白の面積(片面)は
$$
\pi r^2 \times \frac{2\theta}{2\pi} - r^2\sin\theta\cos\theta=r^2\bigg(\theta - \frac{\sin2\theta}{2}\bigg)
(0\leqq\theta\leqq \pi)
$$
となるので、表面積は
$$
2r^2\bigg[\pi-(\theta - \frac{\sin 2\theta}{2}) \bigg] + 2rl(\pi-\theta)
$$
また、体積は
$$
r^2\bigg[\pi-(\theta - \frac{\sin2\theta}{2}) \bigg]l
$$

となります。
よって熟成の進行度(=体積に対する表面積の割合)は
$$
\frac{2r^2\big[\pi-(\theta - \frac{\sin 2\theta}{2}) \big] + 2rl(\pi-\theta) }{r^2\big[\pi-(\theta - \frac{\sin 2\theta}{2}) \big]l}
$$
で、これを計算すると
$$
\frac{2}{l}+\frac{2(\pi-\theta) }{r\big[\pi-(\theta - \frac{\sin 2\theta}{2}) \big]} (5)
$$
となります。式自体は複雑ですが、考え方としてはそんなに難しくありません。
1項目より、$${l}$$が小さければ小さいほど(=樽の高さが小さくなるほど)熟成の進行度は早くなるのはここでも分かります。
また、$${\theta\to0}$$の極限でエンジェルズシェアがない(3)の結果と一致するのも分かります。
エンジェルズシェアが極限まで進んだ状態($${\theta\to\pi}$$)の状況を考えてみましょう。
$${\theta'=\pi-\theta}$$と置くと、(5)式は下記のように書けます。
$$
\frac{2}{l}+\frac{2\theta' }{r\big(\theta' -\frac{\sin 2\theta'}{2} \big)} =\frac{2}{l}+\frac{2}{r\big(1-\frac{\sin 2\theta'}{2\theta'} \big)} (6)
$$
$${\theta\to\pi}$$の極限は$${\theta'\to0}$$と表せるので、エンジェルズシェアが極限まで進むと
$$
\lim_{\theta'\to+0}\frac{\sin 2\theta'}{2\theta'} =1
$$
より(6)式の2項目の分母が0に近づくことで2項目が支配的になり、エンジェルズシェアは加速します。
また、$${r}$$や$${l}$$といった樽自体の大きさのパラメータの熟成の進行度への影響は小さくなり、ここでも同様に樽の大きさによる熟成速度への関与は小さくなると示せました。
余談
$${\theta'}$$が$${0}$$に近づく極限では
$$
1-\frac{\sin 2\theta'}{2\theta'}
$$
が0に近づくのでエンジェルシェアが進み、入れ物自体の大きさの影響を受けにくくなるのは分かったのですが、もう少し詳しく見てみます。(6)式の2項目で$${r}$$を除いた部分の$${\theta'}$$の関数部分のみに着目した
$$
\frac{2}{1-\frac{\sin 2\theta'}{2\theta'}}
$$
のグラフは下記のようになります。
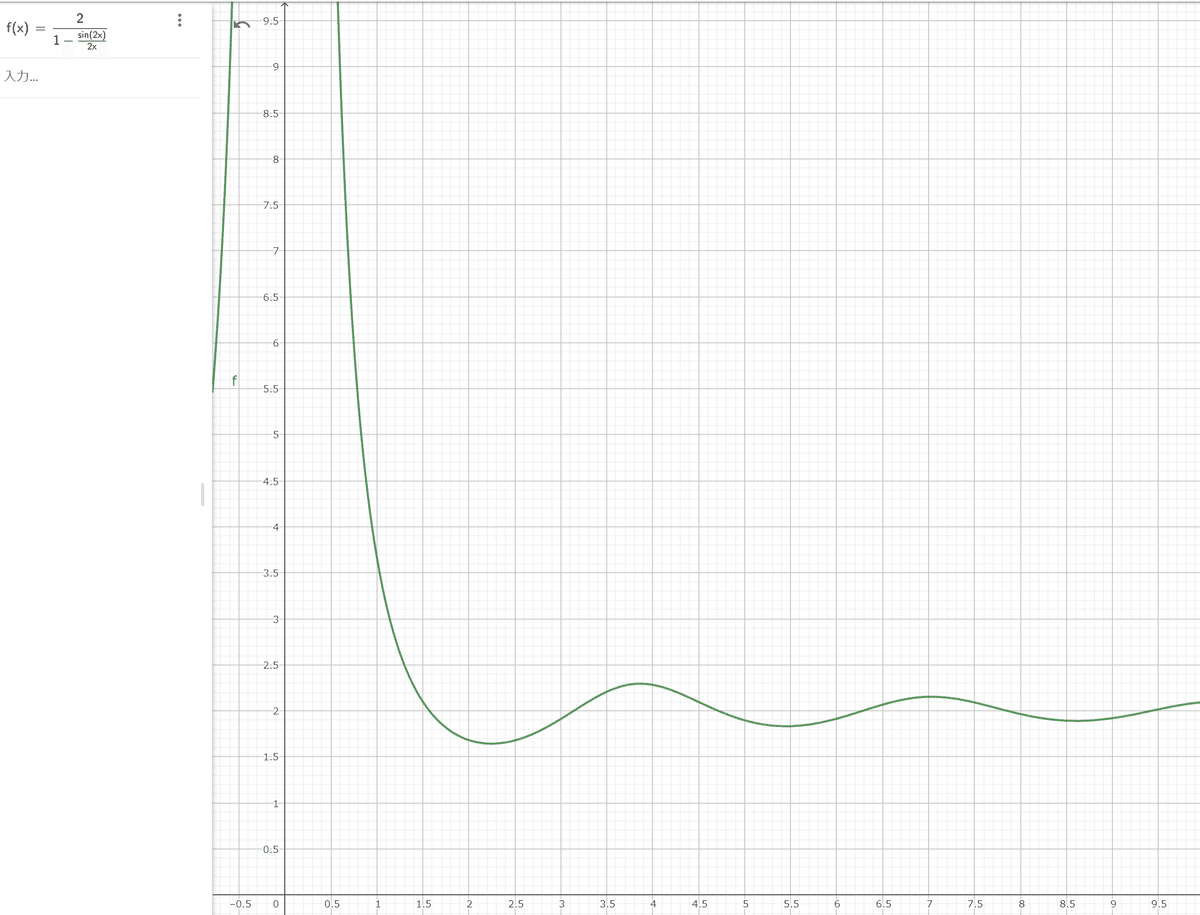
$${\theta'}$$を$${\pi\to0}$$に近づける途中で少し値が減っている箇所があります。これは立方体で見た時と同様に、エンジェルズシェアがある程度までいかないと、入れ物に満タンの状態の時よりも熟成速度が落ちる箇所があるということです。
微分して極値を出せばこの閾値は出すことができますが今回はざっと振る舞いを見るだけなので考えません。興味ある方は(6)式を微分して三角関数の合成などを実施して確かめてみてください。ちなみに$${\theta': \pi\to0}$$の範囲で極値は$${\sqrt{5}\risingdotseq2.23}$$とかになります。
まとめ
「熟成は確かに入れ物が小さければ早く進む。ただし、エンジェルズシェアが進むほど入れ物の小ささの熟成速度の優位性は失われていき、エンジェルズシェアが一定の値を超えて進むと、それ以降エンジェルズシェア自体も加速する」というのが結論です。
要は超高速で熟成させたければ、樽にほんのちょっとだけ液体を入れれば良いわけです。
正直エッセンスを掴んでいただく分には立方体の個所で十分かと思います。
(計算面倒くさかった。。)
円柱よりもさらに実物の樽に近い状態で計算したい方はやってみて下さい。
残課題と所感
今回、熟成は樽と液体が接する部分のみで進むという仮定を置いています。
実際には他にも色々複雑な要素が絡み合って熟成は進むので、より詳細な検討が必要になる可能性があります。
寒い地域の生き物の身体が大きいことと樽の大きさによるお酒の熟成の速さの違いのアナロジー、および、エンジェルズシェアが進んだ時の2乗3乗則の優位性の陥落など、割と書いてて楽しかったです。
謝辞
今回のアイデアの発想や計算の詳細はN大学理学研究科素粒子宇宙物理学専攻同門のT氏とS氏に負うところも多い。
この場をお借りして感謝の意を示させていただく。
