
微積と線形代数だろ。入学したんだから。
こんにちは、パルです。
東工大の電気電子系で現在M1です。量子物性の研究を行いはじめました。
最近マジで忙しい。授業が多いし、課題もまぁまぁある。やりたいこともたくさんあって、遊ぶ時間なんてないですね。挙げ句の果てに、ゲームしたいとすら思わなくなりました。
息抜きはこうしてブログを書いたりYoutubeをみたり、本屋巡りすることですね。本屋巡りは最近あんまり行ってないので行きたいですね。Youtubeは最近はホロライブのVチューバーさんをよくみています。私は見る専でコメントもスパチャもしていないですが、キャストの持ち歌はどれも魅力的で、コンサートとか行ったら楽しそうだなーと思っています。
さて、今日のテーマは理系向け。その中でも
「割と勉強に興味がある人向け」
ですが、
大学に入学したらまずは微分積分と線形代数をやるべき
ということです。
まぁ皆さん理系であれば多くの方がB1のカリキュラムでやっているんだと思いますけれど、今回のテーマは「B1のうちに微積と線形代数に触れましょう」ということではなく、「B1のうちに微積と線形代数をできるだけ完全に理解しようと試みましょう」ということです。
ちなみに、読者さんが文系であってもこの二つの科目についてはやっておいても損はないと思うほどです。
以下、この理由について説明しようと思います。どうかお付き合いくださいませ。
ちなみに、こう偉そうに言ってますが、私自身数学の専門家でもないし、ただの修士課程の学生に過ぎませんので、完全に理解しているとは到底言えません。ただ、だからこそ言わせていただきたいのですが、私が完全に理解できていないのはB1での勉強がしっかりできていなかったからです。
しかし真面目に勉強していなかったというよりは、B1での力不足が原因だったように思えます。私は凡人ですから、1度見てすぐ理解できるほどの頭脳を有する人間ではありません。ですから、習得するのに時間がかかってしまったわけですね。
だからこそ、皆さんにはもっと早くからしっかりと微積や線形代数にチャレンジしてほしいのです。何もいろんな分野をやる必要はなくて、とりあえずこの2分野だけは早めに理解しておく価値があると心から思います。
私の大学生活についてもこちらの記事にまとめてありますので、よければこちらも見ていってくださいね。
微分積分と線形代数の重要性
まず、最初に謝らせてください。この章ではタイトル通り微積と線形代数の重要性について話します。大学のどのような分野で微積と線形代数がどういった形で用いられているのかを見ていきます。
しかし一方で、
「早めにやらないと、そのうち沢山使うことになるのか……やばいな」
とある意味で焦らせてしまう可能性があります。
人によっては、もしかしたら自由な伸び伸びとした勉強ができなくなる可能性がありますので、それが不安な方は次の章「微分積分、線形代数のどこでつまづくのか」から見ることをお勧めします。
微積と線形代数は多くの理系学部で、B1のカリキュラムに採用されている数学科目かと思います。私が学部に入学した頃は微分積分は高校でやっていましたが行列はやっておらず、大学に入ってから非常に苦労した記憶があります。ちなみに私の父の世代は行列を高校で習っていたらしい……
ですから早く行列を高校の学習課程に復活させていただきたいと願っていたわけですが、2022年度からの新学習指導要領がこちら(以下の図)。
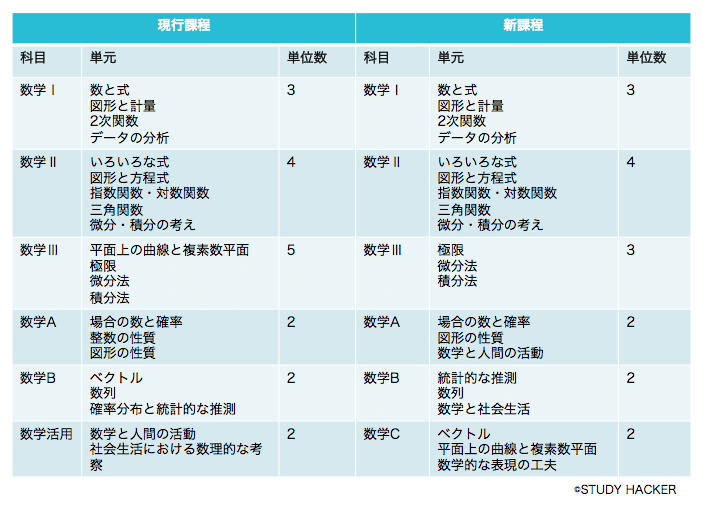
(引用:数学Cが復活。統計が必須化。数学の次期学習指導要領案(2022年度開始)をわかりやすく解説!(大学受験ハッカー))
なんだこれは。文部科学省はベクトルや複素数平面までも必修課程から取り上げるのか。代わりに確率統計が必修科目化したようですが、確率統計こそ大学からやっても問題ないと思うんですけどね……
さて、そんなわけでこれから大学に入学される方は、微積の知識は多少なりともあっても線形代数はほぼやったことがない、と言う方が大半だと思うんですね。
少し余談を挟んでしまった感が否めませんが話を戻して、まずは「なぜ微積と線形がB1のカリキュラムで扱われるのか」という話をしようと思います。完全に私の個人的な意見に過ぎませんが、参考にしてください。
微分積分について
微分積分は解析学ともいいますが、ざっくりと言えば(ユークリッド空間上での)極限$${\lim}$$を使用した色々を扱う分野ですね。微分積分を用いる数学分野はどこかというと、解析学を勉強する分には大体使うと思います。つまり、ユークリッド空間上の解析学は前提が要らないんですが、(複素解析や関数解析、微分形式などといった)もっと違う空間の微分積分を扱おうとすると、ユークリッド空間の微分積分を用いて、あるいは比較して「B1でやった微積のこれと同じことだよね」という感じで持ち出されます。
まぁかなり当たり前な話をしていますが、要するに
B1の分野なので後でやる分野の前提になる
ということです。とは言っても、
「じゃあ自分は電気電子だから要らねーや!数学やらんし。」
となると思ったらそれは大間違いです。電気電子分野では回路を解くと思いますが、回路方程式を定式化するためにフーリエ級数展開やフーリエ変換、ラプラス変換というものを用います。
これ、微積です。
それだけならまだしも、線形代数との融合分野です。
また、数値解析というコンピュータシミュレーションを行う際に必要になる分野がありますが、そもそも数値解析は微積分をコンピュータで扱えるように再定式化する分野です。
とりあえず学部で勉強するだけならまだ耐えるかもしれないですが、研究室で必要になることはあります。
B4でB1の内容を1から勉強するの、結構大変ですよ、本当に。
大体、この記事を書いてる本人が電気電子出身ですからね。
物理学でも大いに微積分は効果を発揮しまして、ほとんど全ての物理理論で用いられます。例えば、
力学:常微分方程式
電磁気学:ベクトル解析
熱力学:偏微分方程式
一般相対性理論:微分形式
などです。そもそも機械科は力学や熱力学の応用分野、電気電子科は電磁気学や量子力学の応用分野と言った感じですので、当然力学や電磁気を勉強することになります。したがって、これらが必要になるわけですね。
なにも、「理論的にしっかり定式化しようと思えば必要になってくる」という話ではないです。むしろそれならもっと色々必要な数学が追加されますが、最低限必要なのを列挙してこれなんです。
こんなにやらないといけないのか…….と思いましたか??
まぁ嘘はつけないので「そうです」というしかないのですが、B1の微分積分さえある程度理解していればB2以降の授業中に応用数学分野はある程度身に付きます。
逆にB1で微分積分の勉強を怠ってしまうと、以降でだいぶ苦労するor理解を諦めるということになりかねないです。
線形代数について
線形代数は、超ざっくり言えばベクトルと行列に関する分野です。もう少ししっかりいうなら、「ベクトルが定義可能な空間上の写像の性質を明らかにする分野」と言えますが、
「写像ってなんすか?」
という方は、ベクトルを回転したり伸ばしたりする分野と考えればとりあえずはOKです。
ですから当然、ベクトルを扱う分野では必要になりますね。
まぁ電磁気学で必要になる「ベクトル解析」は正直高校程度のベクトルの知識で十分かと思うのですが、実はベクトルをしっかり数学的に定義すると高校で習う、
$$
\begin{bmatrix}
x & y & z
\end{bmatrix}
\in \mathbb{R}^3
$$
という実数の組みで得られるベクトル以外に関数自体もベクトルとして見做せることができて、それを利用したものが先ほど説明したフーリエ級数展開といったものです。
電気電子の方はフーリエ級数より前に、初等的な部分ありますが線形代数が必要になりますよ。電気回路の線形回路網、どうやって解析するんでしょうか?
これにはクラメールの公式や行列の基本変形というものを用います。
物理でも、量子力学をやりたい方は本当に真面目に線形代数と向き合う必要が出てきます。量子力学は物理科では必修なので、物理科の線形代数は受けたことがないのでわかりませんが、先生方はかなり必死でB1のうちに教えるんじゃないかと思います。
制御工学 〜「工学」という名の数学分野〜
さて、機械系の方お待たせしました。もしかしたら電気電子からも制御工学という方面に進みたい方はいるかもしれませんが、制御工学という分野は実はかなり数学的な分野です。
そもそも制御工学というと、現代のテクノロジーとして代表する方も多いのではないでしょうか。ロボットやドローン、ロケットの軌道追従など、その辺りは全て制御工学の分野で、将来への展望が期待されていますね。
私はB4時代、ロボット制御の研究をしていたのですが、マジで数学でした。というか、システムの理論構築に興味があって制御を選んだのですが、思った以上に数学で、「そんなのも使うの!?」というほどでした。
私には数学科の友人がいるので、よく数学のどのような分野があるかは友人から効いていました。中には物理学ではほとんど目にしないような、数学理論らしい数学の話もありまして、当時の私は
「ほぇ〜〜〜」
と半分他人事のように聞こえてしまったわけです。しかしなんと制御工学という分野で登場しない数学理論は、少なくとも私が知る限りありません。
もう一度言いますよ?
制御工学では少なくとも私が知る限り、使わない数学はありません。
中にはロボティクス方面に特化しているような研究などもある可能性はありますが、制御理論自体が非常に数学的な言語で説明されるため、制御関連の研究をしている限りはどこかで数学にぶつかると思います。
で、制御工学でももちろん微分積分や線形代数は猛威をふるいます。そもそも制御工学の1つの目標は「システムを安定化させること」です。この「安定化」というのが肝で、まずはどのようなシステムなら安定なのかを定義する必要がありますね。
そこで、例えばリアプノフ安定性という安定性を定義するわけですが、これがそのまま常微分方程式ないしは力学系理論の言葉です。ここで微積分が出てきます。
また、システムが必ずしも扱いやすい性質を持っているとは限らず、非線形性と言った少し扱いにくい性質を持つのが大半です。そんな中でも線形に近似することができる場合があって、ここで線形代数が登場します。
システムが可制御であるとか可観測であるという話もあるのですが、これも線形代数の言葉です。
システムの線形近似に関してはあまり触れていなかったので少し雑になってしまいましたが、おおよそこのようなイメージだと思います。
このように、制御工学をやりたい人は微分積分・線形代数とは切っても切れない関係にあるわけですね。
微分積分、線形代数のどこでつまづくのか
先ほどまでで微積や線形代数が非常に重要な分野であることを見てきたわけですが、そもそもB1の時点で前提知識が必要ない数学としてこの2教科が選ばれているはずなのに、どこでつまづいてるんでしょうか。それについて自分の経験をもとに考えてみました。
なお、以下の考察は私の偏見が9割だと思いますが、ご了承ください。
微分積分の難関ポイント:ε-δ論法
$${\epsilon - \delta}$$論法は、関数の連続性を数学的に定義するものです。
高校数学では$${\lim}$$という極限操作が「十分に近づける」や「限りなく近づける」といった曖昧な表現で済まされていたわけですが、論理学である数学では当然そのようなことは許されません。
ですから、これを厳密に定義するわけですが、そこで最初に登場するのが$${\epsilon - \delta}$$論法かと思います。
数学をやる方は、「$${\epsilon - N}$$論法の方が早かったような……?」と思われるかもしれませんが、$${\epsilon - N}$$論法は数列の概念なので、関数の連続性さえ定義できれば十分な工学系などではあまり扱われないと思います。(少なくとも私の学科は授業では扱われませんでした。)
さて、$${\epsilon - \delta}$$論法とは次のようなものです。
定義
$${x \in \mathbb{R}}$$とする。関数$${f(x)}$$が$${x = a}$$で連続であるとは、
$$
\forall \epsilon > 0, \exist \delta > 0 ~s.t.~ |x - a| < \delta \Rightarrow |f(x) - f(a)| < \epsilon
$$
となるときをいい、このとき$${\lim_{x \to a} f(x) = f(a)}$$とかく。
???????????
と最初はなると思います。この定義は論理式のみで書かれていることが(前提が少ないので)素晴らしいのですが、それが逆に高校数学との差異を生んでしまっているので新入生にはかなり難しいと思います。
もしやる気になったら、こちらをどう解釈すべきかという話もあとで自分の復習も兼ねてnoteにアップロードしたいと思います。
そもそもこの$${\epsilon - \delta}$$論法は数学的には位相空間論に属する分野です。位相空間論は、ざっくりいうと「近さ」をしっかり定義しましょうという分野なのですが、そこで連続写像というものが登場します。
それを連続関数の場合に限定して使う必要があるので、微積を勉強する最初にチラッと登場するわけですが、
「それだけでわかるわけないだろ!!」
と個人的には思います。
これを打破するには、大変かもしれませんがやはり集合論や位相空間を並行して勉強するという突破口をお勧めしたいところです。
とにかく論理式に慣れることが大事です。
集合論、位相空間は数学科がB1でやる内容です。あんまり数学系で初等的な微分積分が辛いという話は聞いたことないのですが、集合・位相の勉強で論理式に慣れていることが原因かと思います。
別に集合・位相を微積の前に勉強する必要は全くありません。他と並行でいいと思いますし、とりあえず後回しでも良いと思います。また、数学科と同程度の理解が必須とも思いませんので、集合も最初だけでいいと思います。具体的には、
共通部分、和集合
写像(単射・全射・全単射)
直積集合
(選択公理)
といった用語の定義がわかる程度であれば十分すぎるくらいだと思います。つまり、松坂本の第1章で十分です。松坂本というのは、
松坂, "集合・位相入門," 岩波書店
という、多くの数学科の教科書でもある(と思う)非常に有名な本の通称です。もちろんこれは古い本ですので、最近の方が記述がわかりやすいという理由で他の本を選んでもOKです。一回通しで集合論をやったことはあるのですが、正直「濃度」や「順序集合」などといった、上で列挙しなかった概念を使ったことはあまりないです。
それくらいなら、早く位相空間をやった方が良いと思います。位相空間はわかっておくと非常に見通しが効くので。
とは言え、正直微分積分は最初の連続性の定義でつまづきやすいだけで、その後の部分でうんうんと唸っている人はあんまりみたことがありません。
テイラー展開や全微分、chain ruleなども最初は「なんだこれ」と思うのですが、物理数学などのより応用的な授業で気持ちを教わって、みんな克服してしまいます。
もちろん物理数学などで教わる全微分は数学的な、いわゆる「微分」という関数を定義する方法ではないのですけれど、正直物理ではそれで十分ですし、困ったことがありません。私も昔勉強しましたが、数学的な定義は恥ずかしながら今パッと出てきません。数学科では「定義が出てこない」というのはかなりの重罪ですね。
対して、$${\epsilon - \delta}$$論法は分からないと困ることがあります。それは、先ほども言った通りこれは「位相」の概念だからです。位相空間を使うとより高度な幾何学が学べます。曲がった空間を扱う幾何学です。これは一般相対性理論に応用されます。
位相以前に集合論自体もやっておくと応用が効いて、例えばルベーグ積分を学べます。通常の積分では可積分とならない関数に対しても積分ができるようになる、別の積分です。実は、フーリエ変換を数学的にしっかり理解しようと思うとここが必要になるのです。
ちなみに、ルベーグ積分は現在私も勉強中です。数の落とし子チャンネルという、素晴らしい講義動画をアップロードしてくださっているチャンネルで毎日勉強しています。
集合・位相についての講義動画もあるようなので、こちらで勉強してみるのも良いと思います。
線形代数の難関ポイント:ベクトル空間
微分積分の一番最初から$${\epsilon - \delta}$$論法という厳密性の刃を振りかざしてくるもんですから、最初は行列演算をするだけの線形代数は非常に単純明快で、心の友のように思うでしょう。
前期の中間で「行列式」というものを習います。2次、3次の行列式は余裕ですが、n次に拡張された瞬間は少し嫌な顔をしてしまうかもしれません。ですが大丈夫。「余因子展開」という別の切り口が救いの手を差し伸べてくれるでしょう。
そもそもn次の一般的な行列式の定義は、行列式に関する証明にしか使ったことないですし。実際に行列式を計算するときは余因子展開必須です。
微積と違って、お前はいいやつだな〜〜!!もう線形代数しか勝たん!!!
そう思った矢先、悲劇が訪れます。
それはB1後期、線形代数の行列式が終わって、続きからまた線形代数を学ばんとするときでした。
定義
$${\lambda,\mu \in \mathbb{R}}$$、$${v,w,z \in V}$$とする。また、演算+およびスカラー倍を、
$$
\forall v, w \in V, v + w \in V \\
\forall \lambda \in \mathbb{R}, \forall v \in V, \lambda v \in V
$$
を満たすものとして定義する。
このとき、$${V}$$が(実)ベクトル空間であるとは、次の1.〜8.を満たすときをいう。
$${v + w = w + v}$$
$${v + (w + z) = (v + w) + z}$$
$${\exist 0 \in V ~s.t.~ \forall v \in V , v + 0 = 0 + v = v}$$
$${\forall v \in V, \exist (-v) \in V ~s.t. v + (-v) = (-v) + v = 0}$$
$${\exist 1 \in \mathbb{R} ~s.t.~ \forall v \in V , 1v = v}$$
$${\lambda(\mu v) = (\lambda \mu) v}$$
$${(\lambda + \mu) v = \lambda v + \mu v}$$
$${\lambda(v + w) = \lambda v + \lambda w}$$
おい。嘘だろ、線形代数。
微積だけじゃなくお前までも俺を裏切るのか……
と、心に壊滅的なダメージを受けてしまう方は少なくないと思います。
前期までの行列式の計算が嘘のように、こちらも非常に抽象的な議論に突入するからです。
ですが、むしろここからが線形代数の始まりなのです。まぁいきなり本性を表したという意味では裏切られたと言えるのかもしれませんが、ここで諦めてしまうと本当にもったいないです。踏ん張りましょう。
まず、この定義はベクトル空間という集合の定義です。定義ということは、これを満たすようなものを持ってくれば、それはベクトルと言えることになりますね。
もちろん我々が高校のうちに習った数ベクトルもこの8つを満たすわけですが、ここでこんな風に関数$${f,g : \mathbb{R} \to \mathbb{R}}$$の和とスカラー倍を定義してみましょう。
$$
(f + g)(x) \coloneqq f(x) + g(x) \\
(\lambda f)(x) \coloneqq \lambda f(x)
$$
こうすると、なんと関数の集合$${\{f\}}$$自体がベクトル空間として見なせるんですね。
これを応用すると、関数が一次独立だとか、関数に内積を定義するとか関数が直交するとか、そんなことが言えるようになるわけです。これがまさにフーリエ級数展開や量子力学のブラケットに応用されていくんです。
(一般には関数のベクトル空間は無限の次元を持って、少し扱いが面倒になります。フーリエ解析や量子力学をやると、無限次元だということや面倒臭さがすぐにわかると思います。)
さて、ここの突破口はなんでしょうね。線形制御とか量子力学とか、とにかく「ベクトル空間が必要になる具体例に触れること」かなと思ってしまいますけれどこれは経験に依るものですから、B1のうちにできることは代数学に触れることかなと思います。
代数学は正直私も勉強途中といったところなのですが、群論、特に加群という話がベクトル空間をより一般的にみることができる概念だと知ってから、ベクトル空間に好感が持てるようになりました。
ベクトル空間の定義の1~4は、「+の演算に対してアーベル群」という話でまとめて考えることができて、私もベクトル空間の公理を書き出す時はこのようにして考えています。1~4がまとまるため、覚えるものが実質5つで済むから覚えやすくなります。
それに電気電子屋さんはあんまり使わないんですが、物理屋さんは結晶構造の話で群論を使うことになりますし、量子力学をやる方はリー群という話をする必要があるのでいずれにせよ後に群論をやることになります。
また、代数学の「有限体」という概念がのちに計算理論でやるブール代数や通信理論で役立つと思います。
まぁとりあえずは群論だけでもやっておくと、いいんじゃないかなと思います。もちろんこれも位相空間と同じで、先にやっておくというよりは並行して進めるのがいいと思います。
まとめ
今回は微積と線形代数がどれだけ重要かについてみた後に、難関ポイントを確認し、それを克服する対策法についてまとめました。
私の難関克服方法は、全体として「違う視点から攻める」といったことに要約されそうです。$${\epsilon - \delta}$$論法では位相から、ベクトル空間では代数学から攻めるといった視点を用意しましたから。やはり、有用な概念が「わかりにくい」というのは全体的に必要な知識が足りていないとか、その前段階にやっておくべき分野の理解が足りないということが多くて、決して「理解能力が足りない」ということはありません。もしそうなら私は何一つ理解できずに終わっています。
仮に、微分積分、線形代数の知識だけで頑張って覚えても同じくらい時間がかかかると思いますので、それくらいなら違う分野も並行してやった方が有用かと思います。
一つ、スケジュールを提案いたしますと、
集合論:前期の空き時間にやる(とりあえず$${\epsilon - \delta}$$は保留にしておく)
位相空間:夏休み期間
代数学:夏休みに群の定義、アーベル群を確認だけしておく。後期終了後、春休み期間に代数を一通りやる
という感じだといいと思います。夏休みに位相空間を終わらせるのは結構大変だと思うので、Youtube や各大学のOCW(Open Course Ware、授業資料や授業動画が載っているサイト)などを活用するのが良いかと思います。
ただ、物理や工学を学ぶ上で大事なのは、代数学よりもはるかに集合・位相だと思います。どんな分野でも使える最強の基本原理です。
私は学部生のうちルベーグ積分や多様体を勉強したかったんですが、本の序文に
この本の予備知識として、集合・位相論の初歩を仮定する。
といったような文が書いてある本がよくありまして、読めなかった悔しい経験がありました。そのようなことを、早いうちからなくしておきましょう。
では、勉強を頑張ってくださいね!!
