
足すとだいたい1になる分数の組み合わせは、なぜだいたい1になるのか(1)
(冒頭のUKイラストは本題とほぼ無関係です)
問題の発端
さて、ちょっと前に下のようなツイートがバズりました。
この写真に写ってるのは、くもん出版から『はじめての分数パズル』という名前で発売されている知育玩具です。1/2、1/3、1/4 といったピースを円形にはめていって、分数の概念を学ぼうという趣旨になっています。
ぼく「いや、そうはならんやろ」
— yugokitajima (@yugokitajima) May 2, 2021
息子「なっとるやろがい」 pic.twitter.com/AVcpOgbZ7r
1/2 は 2 枚、1/3 は 3 枚というように、1/n のピースは1セットに n 枚入っています。同じピースを集めて 1 にしてもいいし、異なるサイズのピースを組み合わせて 1 にすることも可能です。
【 1/2 + 1/3 + 1/6 = 1 】 や 【 1/2 + 1/4 + 1/8 + 1/8 = 1 】といった組み合わせは、皆さんにも馴染みがあることでしょう。
さて、上の写真のなにが面白いかというと、
【 1/3 + 1/4 + 1/6 + 1/7 + 1/9 = 1 】
になっているところです。1/7 なんていう中途半端な数が入ってるのに、なぜうまく型にはまるのか。「そうはならんやろ」と首をかしげながら上の式を通分すると、正しくは
【 1/3 + 1/4 + 1/6 + 1/7 + 1/9 = 253/252 = 1.0040 】
となります。パズルの成形の具合から、ピッタリ 1 にならなくても、0.4% 程度の誤差なら入ってしまうということだったんですね。
さて、このバズツイを受けて、強欲な私は「ほぼ1」になる他の組み合わせも探すことにしました。手元のコンピュータを使って色々なパターンを適当に調べたところ、以下の表のような組み合わせが見つかりました。
なお、『はじめての分数パズル』には 1/11 のピースは存在しません。1/10 の次は 1/12 です。表もそれに合わせています。

この図表には、「和が 0.995 と 1.005 の間に入っているもの」、つまり「1との誤差が 0.5% 以内に収まる組み合わせ」を探して収録しました。どうですか。結構たくさんありますよね。なかなか不思議です。
この表を付けて、先の14万いいねのバズツイにリプしたところ、230のRTと460のいいねがもらえました。まあまあの反応でしょうかね。
でも実のところ、「もうちょっとRTされると思ったんだけどなあ」と残念だったのは内緒です。元ツイに比べて17時間遅れの投稿だったので、バズツイに乗っかるコバンザメ戦術をとるには初動が遅すぎたんですね。
それはともかく、「なぜこの表の組み合わせは『ほぼ1』になるのか?」と思いませんか。その疑問に答えようというのが、この記事の本題です。
足して引いてもほぼ同じ
さて、上の例に出てきた
【 1/3 + 1/4 + 1/6 + 1/7 + 1/9 = 253/252 = 1.0040 】
という式ですが、これを少し変えると、
【 1/3 + 1/4 + 1/6 + 1/8 + 1/8 = 24/24 = 1 】
となって、ちゃんとピッタリ1になります。
これはどういうことかというと、
【 1/7 + 1/9 = 16/63 = 0.254 】と【 1/8 + 1/8 = 1/4 = 0.250 】
の違いです。要するに、分母の (7,9) の組み合わせを (8,8) に変えても、分数の和はだいたい同じになるわけです。
もう少しテクニカルに書いてみましょう。数式嫌いなら下の4行は飛ばしてください。まず、【 1/8 + 1/8 】の同じ数を足すパターンは、
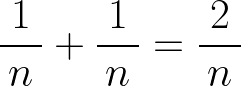
です。次に、分母の数を前後にずらした【 1/7 + 1/9 】のパターンは、
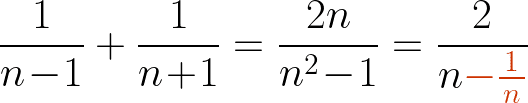
となります。この2式を見比べてみると、色を付けて示した分母の -1/n の分だけ違いが生まれています。n が大きくなると誤差の原因である -1/n はゼロに近づいていくというのがポイントです。上の例のような n=8 くらいの大きさになると、誤差は十分に小さくなり、どちらの分数の和も「ほぼ同じ」と言えるくらいになるわけです。
実際に足し引きしよう
それでは、上に載せた『和がほぼ1』の組み合わせ表を見ていきましょう。まずは左上の例から。対応する部分を色づけしておきます。
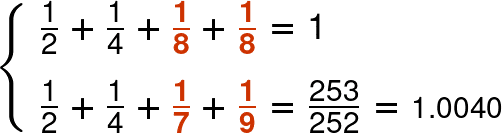
これは既に見たパターンと同じですね。ピッタリ1になる (8,8) の組を、だいたい等しい (7,9) の組に置き換えているわけです。
次は左上から2番目の例。
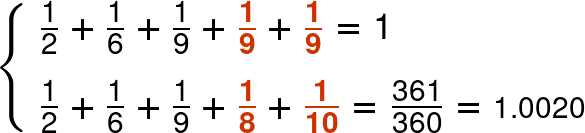
上下見比べてみると、(9,9) の組み合わせが (8,10) に置き換えられています。片方を1減らして他方を1増やすというパターンです。冒頭に紹介した例では n=8 でしたが、このように n=9 でも大丈夫です。
和がちょうど1になる方の【 1/2 + 1/6 + 1/9 + 1/9 + 1/9 = 1 】は、皆さんご存じの 【 1/2 + 1/3 + 1/6 = 1 】 と同じです。【 1/9 + 1/9 + 1/9 】の部分が 1/3 になってるだけですね。
『和がほぼ1』の表の右上に出てくるこの例も同じパターンです。

(8,10) の組み合わせと (9,9) の組み合わせが入れ替わってますね。
上側の和が本当に1になるかどうか確かめたい場合は、
【 1/4 + 1/8 + 1/8 = 1/4 + 1/4 = 1/2 】と
【 1/5 + 1/5 + 1/10 = 0.2 + 0.2 + 0.1 = 1/2 】
を考えれば納得がいくはずです。
2組で足し引き足し引きしよう
ここまでに出てきた「1つ足して1つ引く」というのが最も単純なパターンでした。分母の (8,8) を (7,9) に変換する場合なら、
【 1/8 + 1/8 = 1/4 = 0.250 】と【 1/7 + 1/9 = 16/63 = 0.254 】
になるので、和はおよそ 0.004 増えます。これが最終的に1との誤差になっているわけです。
では、別のパターンはないのでしょうか。分母の (8,8) を (7,9) に対応させるのではなく、大きい方を1つ増やして (7,10) にしてみましょうか。すると、
【 1/8 + 1/8 = 1/4 = 0.250 】と【 1/7 + 1/10 = 17/70 = 0.243 】
になります。和はおよそ 0.007 減りました。
(7,9) の例に比べると、(7,10) の方が少し誤差が大きくなります。0.005 以内に誤差を収めたいという目標から少しはみ出してしまいました。でも実は、この組み合わせにも使い道があります。
(7,9) の例は 0.004 過剰で、(7,10) の方は 0.007 不足なので、これを両方同時に使えば、過剰と不足が相殺して 0.003 程度の不足に収まるのです。それが次の例です。
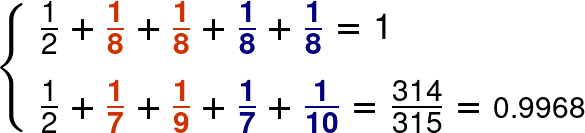
対応する部分を別の色で示しました。「ちょっと多い」を「ちょっと少ない」で埋め合わることによって、全体として「和がほぼ同じ」という目標を実現したわけです。
このようなパターンは『和がほぼ1』の表にたくさん出てきます。
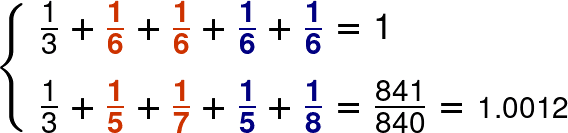
これは (6,6) の1組を (5,7) にして、別の (6,6) を (5,8) にしたパターンです。

この例では、 (6,8) を (7,7) に対応させ、(8,8) を (7,9) に対応させています。片方で少し増えて他方で少し減っている、という仕組みはこれまでの例と同じです。次の4つも似た形式です。




特に2番目の例は【 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + 1/9 = 0.9956 】となっていて、「分母が全部違うにもかかわらず和がほぼ1」になるという、私のお気に入りです。
3組で足し引き足し引きしよう
ここまではペア2組でしたが3組の例もあります。

和が 0.004 ほど増加する (8,8) → (7,9) が2組と、和が 0.007 ほど減少する (8,8) → (7,10) が1組入っています。結果として、下側の式には 3/7 やら 2/9 といった扱いづらそうなのが入ってるにもかかわらず、見事に「和がほぼ1」へと収まりました。
今回のお話はここまでです。
この記事の最初に挙げた『和がほぼ1』の組み合わせ表には、17個の例が載っていますが、ここまでに説明したのは11個です。残り6個は少し違うパターンなので、次回のテーマ(以下リンク)といたしましょう。
ではごきげんよう。
+++++++++++++++++++
