
ゲーム理論を用いたポケモンのすばやさ調整
要約
ポケモンの素早さの努力値振りについてゲーム理論を用いて分析しました。種族値の分布を固定して努力値の振り方を変数としてミニマックス戦略を求めることで、ナッシュ均衡の努力値振りがどうなるかを調べました。
いくつかの種族値分布において計算を行ったところ、ある種族値で人口が多くなるとそれより種族値の大きいポケモンの努力値振りに影響が出る一方で、種族値の低いポケモンへは無振り抜き等の影響は出ていないことがわかりました。
初めに
ポケモン対戦において素早さは超重要です。努力値の調整において抜きたい相手を決めてそれを抜けるくらいまで努力値を振るという行為が日常的に行われます。
ところでわたしは鈍足ポケモンの努力値振りにしばしば悩まされます。とりあえず最速にしたり相手の最速を抜けるように調整すれば良い高速ポケモンと違い、無振り基準の調整はちょっと振るだけで容易に調整を狂わされます。
どの程度まで振るのが効率的なのでしょうか?気になったのでゲーム理論のミニマックス戦略を用いて調査してみました。
だいぶ長くなるので面倒な人は理論解説は飛ばしてもいいかもしれません。それでも長い方はパルス型の計算結果のところだけでも読んでいってもらえると嬉しい。
理論・解説
ナッシュ均衡
ゲーム理論詳しく知らない人の為にナッシュ均衡やミニマックス戦略という概念について説明します。ここに関しては正直わたしも専門じゃないので詳しい説明は別の記事を探してもらいたいです。
ナッシュ均衡とは、ゲーム理論において2人以上のプレイヤーが参加する非協力ゲームにおいて、各プレイヤーが自分の行動を最適化した結果、互いに最善の選択をしている状態のことを指します。つまり、どのプレイヤーも自分の行動を変えることができないような状態であり、この状態が安定しているということです。今回、ゲーム理論的な最適解としてこのナッシュ均衡を与えるような努力値振りを求めるのを目標にします。
ポケモン対戦のように2人のプレイヤーが対戦し、1人が勝ち、もう1人が負けるという結果が必ず出るゲームのことを二人零和ゲームと呼びます。勝者の利得と敗者の利得の合計が常に0になるため、ゼロ和ゲームと呼ばれます。
ミニマックス戦略とは、自分が取る行動に対して相手がとる行動によって最悪の結果を避けることを目的とした戦略です。つまり、相手が自分にとって最も不利な行動をとった場合でも、自分にとって最も有利な行動をとることができるように行動を決定します。
じゃんけんで例えると、グーを出すとパーを出された時負け、チョキを出すとグーを出された時負けるため、相手がどんな戦略を取った時でも50%の勝率を保証するためにグーチョキパーを1/3ずつの確率で出すような戦略がミニマックス戦略になります。
2人ゼロ和ゲームにおいてナッシュ均衡を求める場合、ミニマックス戦略を用いることができることが知られています。つまり相手に最悪な手を出させれることを想定して戦略を考えただけなのに、自分も相手もこれ以上最適化できないような安定な状態を求めることができます。
素早さ調整
ポケモン詳しく知らない人のためにポケモンの素早さについて解説します。
ポケモンにはポケモンの種類ごとに決まった種族値とプレイヤーが調節することのできる努力値という値が存在し、これらの和によって素早さの実数値が決まります。この素早さが実数値で1でも大きいと先制攻撃をすることができ大きな利益をもたらす一方で、それ以上過剰に振っても利益はありません。
つまり相手の素早さより少しだけ大きくなるように調整し、勝てない時は完全に素早さを諦めてその分他の能力を上げることが理想になります。
今回は出すポケモンの種族値の分布があらかじめ決まっているとしたうえで素早さの努力値振りを考えます。種族値を変えるためにはポケモン自体を変えねばならず、習得技や特性タイプなど様々な要素と絡むため容易には変更できない一方で、努力値だけなら変更が容易であり、メタが回るのが早いと考えられるからです。
計算式
次のように変数を定めます。
$$
x:すばやさ実数値\\
S:すばやさ種族値\\
i:努力値で伸びるすばやさ\\
f(S):すばやさ種族値分布\\
g(x):すばやさ実数値分布\\
E(S,i):種族値Sのポケモンの努力値分布。努力値をi振ったポケモンがどれだけいるか。\\
A(x,x'):素早さ実数値xのポケモンがx'のポケモンと対面した時の利益
$$
実際のポケモンでは種族値や努力値から実数値を計算する計算式は次のようになります。なお実数値$${x}$$、種族値$${S}$$、努力値$${i}$$です。
$$
x=S+(i+4)/8+20
$$
しかし今回は簡単のため細かい定数等を省いて実数値=種族値+努力値で計算できるとして扱います。数字はでたらめになりますが、どういう時に増えるかといった定性的な性質は再現できるはずです。また努力値で上がる能力値は実際には0から31までありますが、簡単のため0,1,2,3の4段階で計算を行います。
$$
x=S+i
$$
この時実数値の分布$${g(x)}$$は種族値S+努力値iがxになるようなSとiの組み合わせ全てについて種族値と努力値の分布の積を足し合わせることで計算できます。つまり以下のようになります。
$$
g(x)=\sum_{S} f(S)E(S,i) \\
$$
ここで$${S}$$は実数値$${x}$$になるような努力値振りが存在する全ての種族値について和を取ります。今回は実数値=種族値+努力値で計算しているので次のように書けます
$$
g(x)=\sum_{i=0,1,2,3} f(x-i)E(x-i,i)
$$
このとき次で定義する評価関数evを最大化するような努力値の振り方$${E(S,i)}$$を探します。ただし$${A(x,x')}$$は素早さ実数値xのポケモンがx'のポケモンと対面した時の利益です。
$$
\text{ev}=\sum_{x,x'} g(x)A(x,x')g^*(x')
$$
ここで相手の分布を$${g^*(x)}$$のように$${*}$$を付けて表しました。相手の実数値分布もこちらの実数値分布と同じように種族値分布と努力値分布の積をとることで計算しますが、種族値分布$${f^*(S)}$$に関してはこちらの分布と同じ$${f(S)}$$を用います。$${g^*(x)=\sum_{i=0,1,2,3} f(x-i)E^*(x-i,i)}$$。
今回は利得$${A}$$を次のように定めます。
相手より素早さが高かったら1、低かったら0の利益がある。同速なら0.5
素早さに努力値を振るとその分他の能力値に振れなくなるため微不利になる。このコストは努力値1増やすために$${\epsilon}$$必要とする。
まとめると次のようになります。
$$
A(x,x')=\theta(x-x') -\epsilon\times(x-x')\\
\theta(x)=\begin{cases} 1 &x>0 \\ 0&x<0 \\\frac12 &x=0 \end{cases}
$$
$${\theta(x)}$$が難しそうに見えるかもですが相手より速かったら1、遅かったら0を数式で書いただけです。
このAを使って評価関数を書くと次のようになります
$$
\text{ev}=\sum_{x,x'}g(x)g^*(x')\theta(x-x')-\epsilon\sum_{x,x'}(x-x')g(x)g^*(x')\\
=\sum_{x>x'}g(x)g^*(x')-\epsilon\sum_{x}xg(x)+\epsilon\sum_{x'}x'g^*(x')
$$
$${f(S)}$$を固定して努力値の振り方のみを変えることでevのミニマックス戦略を求めます。ミニマックスの求め方は線形計画法を用いて求めました。
零和ゲームではミニマックス戦略がナッシュ均衡になるため、これで求めた努力値振りを”ゲーム理論における最適解”として考察します。
計算方法
パラメータの違い
努力値を振るコストのパラメータ$${\epsilon}$$を適切な大きさにしないとめちゃくちゃなグラフが返ってきてしまう可能性があります。$${f(x)}$$が一様分布の時について$${\epsilon}$$の大きさを色々変えて振る舞いを調べました。
種族値の分布
調べる種族値の分布として次のような分布を調査します。
ステップ $${y=1 (x_0 \lt x) ,0 (x\lt x_0)}$$
逆ステップ$${y=1 (x \lt x_0) ,0 (x_0\lt x)}$$
パルス $${y=1 (x = x_0) ,0 (x\lt x_0,x_0\lt x)}$$
以上の3通りの分布に対してゲーム理論的にはどのような努力値振りがふさわしいのかを理論のところで述べたような手法を用いて計算しました。
グラフの読み方
計算に用いる種族値の分布を黒の折れ線で、その種族値分布における努力値振りの計算結果を棒グラフで表現することとします。例えば一様分布では次のようなグラフが出来ます。

黒の折れ線が一定値になっており一様分布の計算であることを表しています。また、種族値ごとの最適な努力値振りが棒グラフで表されています。努力値を4段階で振ることにしたので$${i=0}$$から$${i=3}$$まで青から赤で色分けされており、赤が多い種族値ではほとんどのポケモンが最速に振られており、青が多いポケモンでは無振りの努力値振りが最適になっていることを表しています。
上の例では種族値26以上くらいの速いポケモンでは棒グラフが真っ赤になっているので全員最速振りになっていることがわかります。一方で種族値1などの遅いポケモンでは棒グラフは青の割合が多く、無振りのポケモンが多い事を表しています。
計算結果
パラメータの違い
εを大きくしすぎると全員が無振りという結果になり、逆にεを小さくしすぎると全員が最速にするという結果になりました。意味のある結果を得たいなら中間くらいの適切な値を選択する必要があることがわかります。

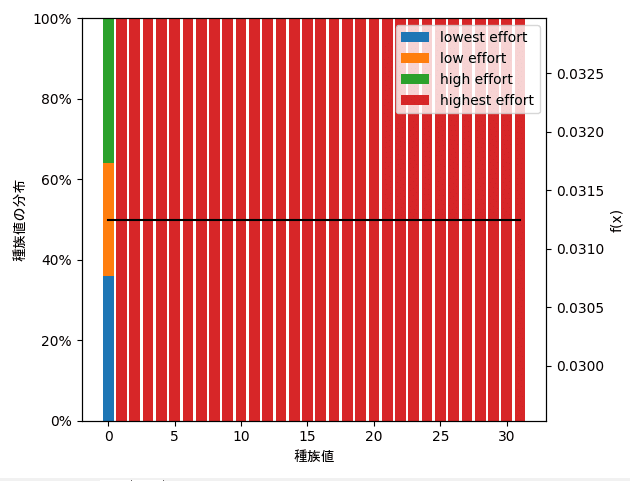
また、中間くらいの設定にすると高速側のポケモンが全員最速になる一方で鈍足側のポケモンは様々な振り方が同居するグラフが得られます。

他方εを上げていっても左側から全員真っ青になるという現象は起こらず、早いポケモンも遅いポケモンも同時に青くなっていくという振る舞いをしました。つまりパラメータを変えた時の振る舞いが高速側と鈍足側で異なります。

分布毎の努力値振り
1.ステップ型
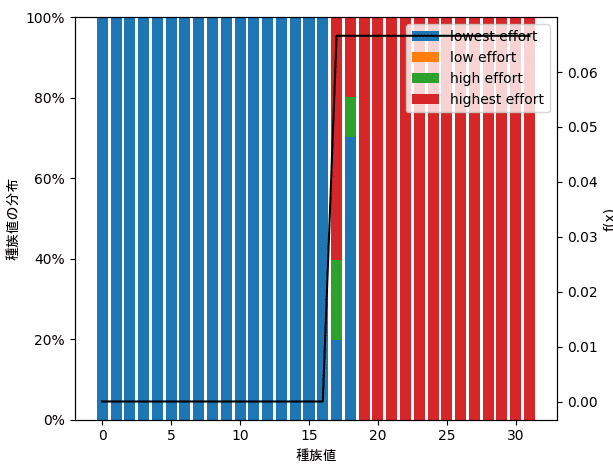
種族値の閾値を境に努力値振りの傾向も切り替わりました。詳しく見ると閾値の右側が移行領域になり、赤青緑のように様々な努力値振りが混ざった振り方が続いた後で最速振りが多くなりました。
2.逆ステップ型


これも種族値の閾値を境に努力値の振り方が変わり、閾値の右側が移行領域になりました。移行領域の振る舞いがステップ型の場合と異なり、赤一色→緑一色→黄一色→・・・というように色を揃えて移行してることがわかります。
3.パルス型
ここの結果が最重要かつ、努力値を振るコストεの大きさによって議論が変わってきそうなのでいくつか書きます。

明らかにパルスの上側と下側とで努力値の振り方が変わっています。パルスより下側では全員無振りになっているのに対し、パルスの閾値より速い側のポケモンは努力値を振る必要が生じています。


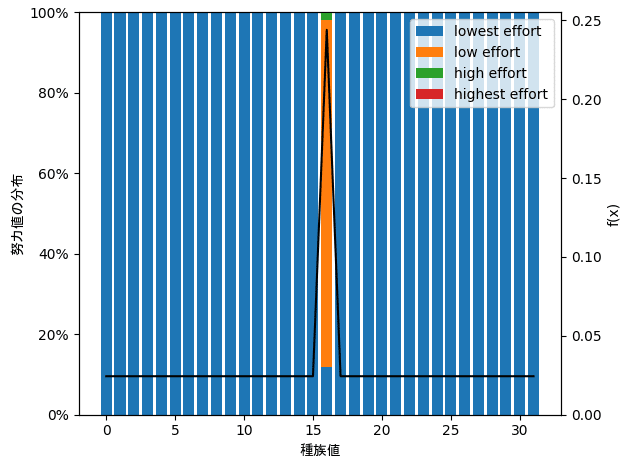
εを変えた結果は以上のようになりました。いずれもパルスの右側と左側で必要な努力値が異なってきており、速いポケモンは努力値を多く振り遅いポケモンは素早さに無振りで他の能力に振り分けるのがベストという結果になっています。
またε=0.036の結果ではパルスより下やパルスのずっと上のポケモンは無振りになるような環境なのにも関わらず、パルスのすぐ上のポケモンだけ最速になる現象が発生しています。
考察
努力値を振るコスト$${\epsilon}$$を変えた実験では$${\epsilon}$$を増やして無振りが増える時の振る舞いと、$${\epsilon}$$を減らして最速が増える時の振る舞いとで振る舞いが異なるという結果が得られました。
これは努力値を増やした時の利益と減らした時の利益とで非対称になっていることに起因していると考えられます。努力値を増やす時は相手を1でも超えれば大きな利益が得られそれ以上の努力値振りは無駄になる一方で、努力値を減らす時の利益は相手の素早さにかかわらず常に一定量の努力値を他の努力値に振れる、と増やした時と減らした時で非対称になっています。
ステップ型と逆ステップ型では努力値振りの傾向が異なる結果が得られました。種族値Sでステップ型になっている場合は最速と無振りの境界になっている移行領域の種族値のポケモンの努力値振りは色んな振り方の混ざった棒グラフになっています。一方、種族値Sで逆ステップ型になっている分布に関しては、S+1では全員が最速より一つ遅い努力値振り、S+2では全員がそれより一つ遅い努力値振りの棒グラフになっており、棒グラフが一つの振り方で占領されたグラフになっているという点で異なります。
一方ステップ型と逆ステップ型で共通することとして人口が多くなっているところの右側=種族値が速いポケモンのところに移行領域ができました。
つまり種族値の遅いポケモンは種族値の分布が大きく変わった影響を受けずに、種族値の大きい側で影響が出ています。
種族値Sでパルス型になっているような分布に関して、最速Sを抜くためにSより少し上のポケモンで最速の割合が増える現象が見られました。これは本来なら最速の努力値振りしないような場合も種族値Sに大量のポケモンがいることでそれを抜くメリットが努力値を振るコストを上回るからだと考えられます。また、Sを抜くためにS+1に最速が増えるとそれに勝つためにS+2も最速にせねばならず・・・というのを繰り返すことでS+1以上の種族値のポケモンでも最速振りが増えていると考えられます。
一方、パルスのすぐ下のポケモンの努力値振りが多めになることはなく、無振り抜きの調整と解釈できるような結果は見られませんでした。努力値振るコストが高い場合はパルスのピークのポケモンが最速になるため抜くことが出来ず、逆にパルスのピークのポケモンが無振りになるほど努力値振りにコストがかかる環境ではすぐ下のポケモンが抜くための努力値振りを割くことができないからだと考えられます。
以上を総合すると、ある種族値のポケモンが多くなるor少なくなるとその種族値より種族値上のポケモンでは対抗して最速になったり手を抜いて少し遅くなる努力値振りが見られる一方で、多いポケモンより遅い種族値のポケモンには無振りを抜くための努力値振りなどの影響は出ていないことがわかります。
結論・まとめ
ゲーム理論を用いて最適な努力値振りの仕方を計算しました。
↑の結果、あるポケモンが多くなる時多いポケモンの種族値より少し早いポケモンで最速○○抜きは有効な一方で、その種族値より遅いポケモンが無振り○○抜きをする振り方は見られませんでした。
端的にいうとS種族値上のポケモン見て努力調整する必要はなく、下のポケモンに抜かれないように努力値振りを決めるべきです。
あとがき
長文お付き合いいただきありがとうございました。文章を書くのが苦手で少し(かなり?)読みにくい文章になってしまったかもしれませんがご容赦を・・・
ポケモン対戦において素早さをどこまで振るかというのは悩むことがわたし自身悩むことが多く、ガチで計算したらどうなるのだろうと思い計算してみました。やや抽象的な結論ではありますが、読者の方に何か得るものがあれば幸いです。
意見・批判・質問等ありましたらTwitter@pyran19まで連絡していただけると感激して対応させていただきます。
