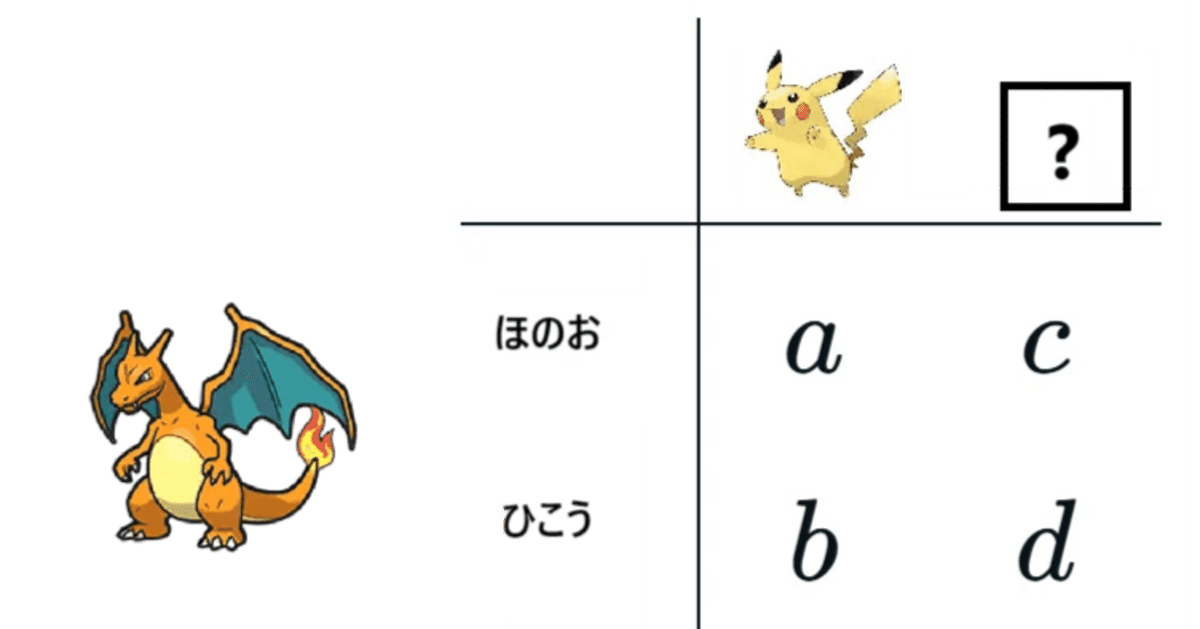
見出し画像

複合タイプ同士のポケモンの相性評価

ぴらん

こんにちぴらーーん

他の計算で使用するために突貫で行った結果が面白くなりそうなのでとりあえず公開しておきます。今回は読み物というより自分が後で見返すためのノートみたいな感じなので読みにくかったらごめんなさい。

序


ポケモン対戦をやっているとどのポケモンがどのポケモンに有利かということをある程度定量的に表したいという需要が発生します。

有利不利を考える上で重要な要素として、ポケモンにはタイプ相性があります。ゼニガメはヒトカゲに強いです。ゼニガメの水技はヒトカゲに２倍のダメージを与えられますし、ヒトカゲ自慢の炎技はゼニガメに1/2倍になってしまいます。

タイプを使って有利不利を決めてあげようと思うと複合タイプに対して少し困ります。例えばエンペルトとゴウカザルで考えてみましょう。さっきと同様にエンペルトが水技２倍でゴウカザルを殴れてエンペルト有利かと思いきや、今度はゴウカザル側も格闘技でエンペルトを殴れます。

このように複合タイプは２種類のタイプ一致技がある点でどっちがどれだけ有利かがわかりにくくなります。今回は複合タイプの相性関係について定量的に評価することを目標にしたいと思います。

先行研究

相性からポケモン同士の有利不利を定量できるとどんな嬉しいことがあるのかという例で最強タイプの決定という話題があります。

遺伝的アルゴリズムやゲーム理論、グラフ理論など様々なアルゴリズムで最強のタイプを決めようとする研究がありますが、これらを行う上で地味に大事な要素としてどのタイプがどのタイプにどの程度有利かというのをどう計算するかという問題があります。つまり今回の記事の内容です。

[1] ポケモン界における最強タイプを遺伝的アルゴリズムで求めてみた

[2] ポケモンの最強タイプを考える【グラフ理論】

[3] ポケモンで最強のタイプはどれか？~ゲーム理論的アプローチ~

それぞれの研究におけるタイプ間の相性の計算方法を抜き出すと以下のようになります。

[1]では、xというタイプに対してyというタイプが与えるダメージ倍率を$${M_{y,x}}$$として、有利さを次の$${h((w,x),(y,z))}$$で定めています。

$$
g((w,x),(y,z))=\max{(f(w,(y,z)),f(x,(y,z)))}=\max{(M_{wy}M_{wz},M_{xy}M_{xz})}\\
h((w,x),(y,z)) = \log_{2}\frac{\max{(g((w,x),(y,z)),\frac{1}{8})}}{\max{(g((y,z),(w,x)),\frac{1}{8})}}
$$

また[2]では以下の画像のような計算式で計算しています。

[2]の勝利確率計算式

一見恣意的な決め方をしているように見えますが、よく見るとダメージが倍変わるごとに勝率確率が10％増減している（効果なし除く）ので、[1]と同様対数ベースの計算式を使っていることと等価になっています。

[3]については以下のような計算式で計算しています。

$${
g((w,x),(y,z))=\max{(f(w,(y,z)),f(x,(y,z)))}=\max{(M_{wy}M_{wz},M_{xy}M_{xz})}
}$$

ポケモンの最強タイプを考える【グラフ理論】

攻撃効果率－防御効果率がポイントとして勝者に与えられる（効果率と呼びます）

例えば、プレイヤ1が炎タイプ、プレイヤ2が草タイプを出した場合、炎→草が2倍で、草→炎が0.5倍であり、炎タイプ（プレイヤ1）の勝ちになります。そして、2-0.5=1.5ポイントがプレイヤ1に与えられます。

seytwoのブログ

以上のように他の研究をするためにタイプに応じて有利さの度合いを設定することが求められることは多いです。しかし、上記の記事の間でも有利度の定義方法にばらつきがあります。どのように定義するのが適当でしょうか。

単タイプの有利不利の定量

まずは単タイプ同士の相性から考えていきます。

ところでポケモンは自分の体力が０になる前に相手の体力を０にするゲームです。被ダメージを半分に抑えると体力が０になるまでに攻撃できる回数が２倍になりますし、与ダメージを２倍にできると相手の体力が０になるまでに受けるダメージが半分になります。つまり与ダメージのｘ倍と被ダメージの1/xが同等の効果を持っているゲームになります。

したがって有利さを表す関数$${v}$$は与ダメージAと被ダメージDの比の関数になっていると考えるのが自然です。

$$
v(A,D)=f\left(\frac{A}{D}\right)
$$

また攻防を入れ替えた時に対称に有利不利が入れ替わってほしいのでAとDの入れ替えに対して符号が入れ替わることも要求されます。

$$
v(D,A)=-v(A,D)
$$

以上二つの条件を同時に満たすためには有利度は$${log(A/D)}$$の奇関数である必要があります。

$$
v=g(\log (A/D))  \tag{gは奇関数}
$$

したがって単タイプ同士の場合の有利さの度合いがどんな形であるか決めることができました。

色々考えましたがこれ以上具体的な関数形を求めるには、有利度をどのように扱うかによって変わってくるところでもあると思うので(先行研究でいうとゲーム理論を使うか、グラフ理論を使うか等でどのように有利度を定義するべきか異なってくる)で単タイプの有利度についてはここまでにします。

以下最も単純な奇関数ということで$${g(x)=\log_2 (x)}$$で話を進めます。

複合タイプ:有利な技だけ打つ場合

さて複合タイプについてです。複合タイプはタイプが二つあるので単純に「炎タイプのポケモンは炎タイプで攻撃する」のような考え方をするわけにはいきません。

このゲームは二つ技を持っていてもどちらか一方しか打つことができないため、とりあえず互いのプレイヤーはタイプ一致技のうち相手に有効な方を使うことにしてみます。

このとき$${A \to \max(A_1,A_2)}$$のように書き換えればよいので次のようになります。($${A_1,A_2}$$は自分のタイプふたつの攻撃する時の倍率)

$$
v = \log_2\left(\frac{\max(A_1,A_2)}{\max(D_1,D_2)}\right)
$$


複合タイプ:タイプ一致技を両方考慮する場合

通る方の技のみを選択するアプローチは一見よさそうに見えますが、実際の対戦を考えるとポケモンを交換する時やこだわりアイテムを持っている時などの運用のしやすさが大きく変わります。

また二つのタイプを両方半減できるポケモンというのはかなり少なく、ほとんどのポケモンが等倍以上で攻撃できてしまう→たくさん半減できて強いタイプというのがなくなってしまうという問題があります。

(実際これらの計算方式を採用してる先行研究[1][2][3]では少耐性少弱点のタイプがやたら強く出ています)

以下Twitterのやりとり

つまり、片方のタイプで抜群つけるとして、もう片方の技でも抜群突けてどっちでも自由に打てるポケモンと他方の技が効果は無いようだで一つの技しか使えないポケモンとでは交代等の読みあいの面で有利さの度合いが大きく違ってくるはずです。

読みあいを考慮して有利さを定量するにはどうすればいいでしょうか？ちょうど過去のゲーム理論の考察の結果が使えそうです。

上記の記事のように２×２の行列でゲーム理論の計算を行うと、交代先のポケモンとの読みあいも考慮して有利度を考えられると考えました。上記の記事によると二つの技を打ち分ける場合の評価は次のようになります

$$
P=\begin{cases} \frac{ad-bc}{a−b−c+d}​& (a-b)(c-d)<0かつ(a-c)(b-d)<0  ・・・(1)\\
a     & b<aかつ(1)の条件を満たさない\\
b    & a<b かつ(1)の条件を満たさない
\end{cases}
$$

となります。ここで$${a,b,c,d}$$は↓図のように二つ技を打ち分けるときのダメージです。

リザードンがピカチュウにタイプ一致技を打つ

ただし、ピカチュウに対する有利不利を定義したいわけなので交代安定になるような状況は除外してます($${a\gt cかつb\gt d}$$みたいなのは除くということ)。

$${c,d}$$はピカチュウ側の交代先なので定数だと思って、$${a}$$と$${b}$$がそれぞれ炎技打った時の１倍と飛行技打った時の0.5倍のイメージです。

上式をaやbの関数として見たとき、下図のように$${a,b}$$の値によって単純に$${a,b}$$のいずれかになる領域と(1)式の複雑な関数になる領域に分かれます。

$${a<c}$$の領域では$${b=a}$$を超えるかどうかで$${b}$$の倍率のダメージが与えられるか、$${a}$$の倍率のダメージが与えられるかが変わってきます。つまり$${P=\max{(a,b)}}$$となって前節の有利な方の技を打つ場合になります。


$${c \lt a}$$となって(1)の領域に入ると$${P}$$の挙動が複雑になります。$${b=a}$$の付近を調べましょう。$${|a-b| \ll |c-d|}$$の条件で(1)の$${P=(ad-bc)/(a+d-b-c)}$$を近似してみます。

一般的に$${X\gg \epsilon}$$の時$${1/(x-\epsilon)=1/X+\epsilon/X^2+O(\epsilon^2)}$$と近似できますから分母の部分は$${-1/(c-d)+(a-b)/(c-d)^2}$$で近似しちゃえます。

また、分子は$${-a(c-d)+c(a-b)}$$と変形できます。これらの計算を合わせて$${a-b}$$が大きいことを考慮すると$${a-b}$$の一次までを残して次のように近似できます。

$$
P=\frac{ad-bc}{a+d-b-c}\\
=(a(c-d)-c(a-b))\left(\frac1{c-d}+\frac{a-b}{(c-d)^2}\right)\\
=a-\frac{(a-c)(a-b)}{d-c}\\
=a-\theta(a-b)
$$

ここで$${\theta=\frac{a-c}{c-d}}$$と置きました。$${a,c}$$は交代前後のダメージですから$${a-c}$$が大きいほど居座った時と比べて交代した時のリスクが小さくなり、相手は交代しやすくなります。したがって$${c-d}$$と比べて$${a-c}$$がどれだけ大きいかを表している$${\theta}$$はどれだけサイクル的な構築に寄っているかのパラメータであるとみなせます。とりあえず$${\theta}$$のことをサイクルパラメータと呼ぶことにします。

まとめると次のようになります。

  • $${a \lt c}$$で相手が交代しにくい時は$${P=\max(a,b)}$$で二つの技のうち通りやすい方の倍率で計算することに相当→従来の結果

  • $${c \lt a}$$で相手側が交代できるようになってくると$${a\to a-\theta(a-b)}$$と通らない方の倍率も計算式の中に入ってくるようになる。この時、通らない方の技にかかる係数は構築のサイクル性が大きいほど大きくなる。

具体例

ややこしいので具体例を考えます。

リザードンがピカチュウにタイプ一致技を打つ

ピカチュウ側の構築が交代できないような構築だと$${a\lt c}$$でリザードンが与えるダメージは$${\max(a,b)=\max(炎技の１倍,飛行技の0.5倍)}$$で通る方の炎技の倍率だけで決まって１倍のダメージが与えられることになります。

一方でピカチュウ側の構築のサイクル性が高くなってくると与えるダメージが0.9×１倍炎技の倍率+0.1×0.5倍飛行技の倍率といったように低い方のダメージの倍率も加算されてくるというのが今回の計算結果です。

これは炎技の方が通っているように見えても交換先のポケモンやこだわりを考慮して飛行技を打ちたい場面も考慮してることに対応します。

通らない方の倍率がどれだけの比率で加算されるかはサイクルパラメータ$${θ}$$で決定され、互いの構築がどれだけ交代を行いやすいかによって変わってきます。

こうして与えるダメージの倍率を計算しなおしたのでこれを使って有利度を計算すると次のように有利度を計算できます。(サイクルパラメータを$${\theta=0.1}$$とした場合)

$$
(有利度)=v=\log_2\left(\frac{0.9\times1+0.1\times0.5}{0.9\times2+0.1\times 0}\right)=-0.92
$$

というようにリザードン側が不利なことを計算できます。

結

複合タイプの場合の有利不利をどのように定量化するかを考察しました。

互いのサイクル構築っぽさによって有利不利の程度が変わってくるのは面白い結果かと思います。

いいなと思ったら応援しよう！