
ポケモンSV:レートの人口分布調査
こんにちは。ポケモンSVのレートがどんな分布になっているか調査したので簡潔にまとめます。
今回は読み物として書いてないので簡潔に。
データ収集
Pokemon HomeのデータからS1とS17のトレーナーデータを収集しました。最初のシーズンとレギュレーションFの最終シーズン、つまり伝説のいない最後のシーズンのデータです。
順位ごとのレート値の分布は次のようになります。レート値は1000倍して小数点を消したものとなっています。
分布の分析
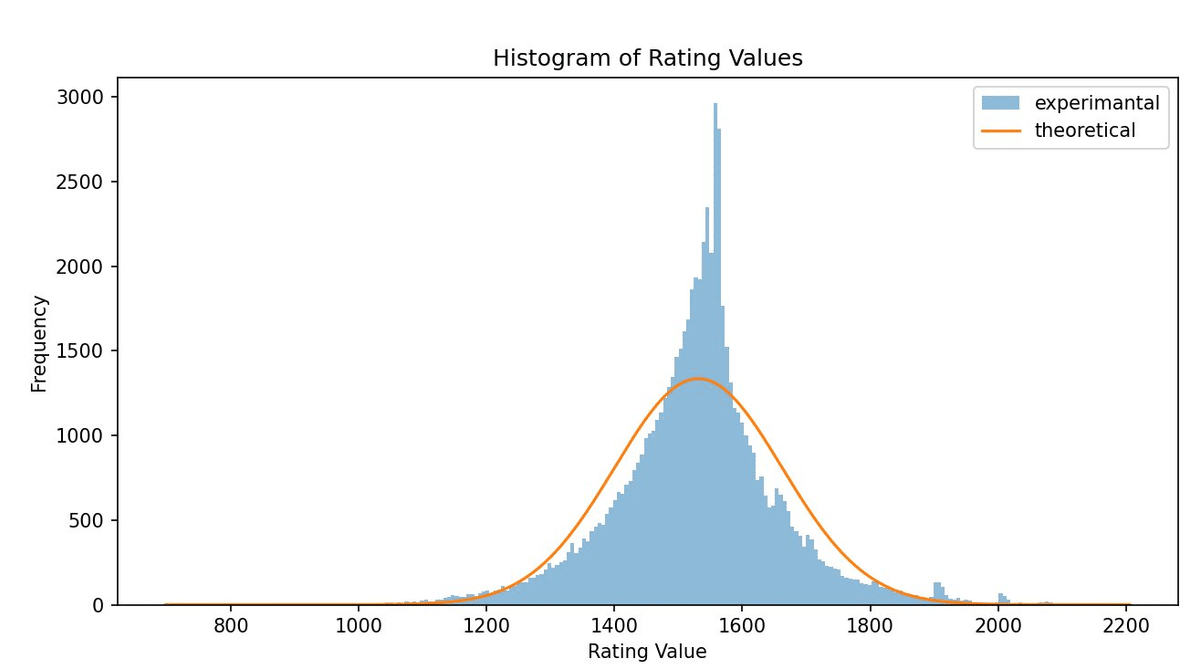
結果を素直にヒストグラムにすると以下のようになります。

一見シンプルな正規分布のようですが重ねてみると次のように結構違う形状であることに気づきます。以下S17について考察
正規分布じゃなきゃどんな分布なんだろ?といろいろ探してみた結果対数を取ってみると面白いグラフになることがわかりました。

なぜかはよくわからないけど対数とるときれいに直線になるのですよね。考察待ってます。

グラフの頂点で微分係数が不連続になる理由については推測ができます。データはマスターボール級の人だけ(ランクマ参加者全体で234,437人に対してマスターボール級到達者は72,682人)です。一定以下の実力の人がグラフに反映される確率は大きく減衰することになります。
つまり一定のレートを境に次のように関数形が変わってきます。
$$
f(x)=\begin{cases}
レートがxの人の数& (x > x_0)\\
レートがxの人の数\times xの人のマスボ到達率 & (x< x_0)
\end{cases}
$$
関数形が閾値で急に変わるからグラフの傾きも不連続に変化するねって理屈です。
モデルの作成
何はともあれシミュレーションのためにも分布関数を作成します。
$$
\ln f(x) = \begin{cases}
-a (x-1500) +b & x<x_0\\
a (x-1500)+b & x > x_0
\end{cases}
$$
ここで、$${a}$$はシーズンによって変わらない定数、$${b}$$は参加トレーナー数に応じてスケールする定数とします。
$$
f(x) = \begin{cases}
C\times e^{-a (x-1500) } & x<x_0\\
C\times e^{a (x-1500)} & x > x_0
\end{cases}
$$
f(x)の積分値がプレーヤー数Nに一致するように定数をスケールすると次式でモデル化できます$${x_0}$$をマスボ級プレイヤーの平均レートとします。
$$
f(x) = \begin{cases}
\frac{Na}{2} \times e^{-a (x-x_0) } & x<x_0\\
\frac{Na}{2} \times e^{a (x-x_0)} & x > x_0
\end{cases}
$$
グラフにフィティングしてa=0.01となるので次回以降のシミュレーションではこれらの関数を使います。
モデルの検証
上記のモデルはS17のグラフを見て考察しました。他のシーズンのグラフに対しても上記のモデルで作成したグラフが実測値を再現できるか検証します。
パラメータは$${a}$$を0.01で固定してプレイヤーの人数やレート平均は実測値から定まるので調査するシーズンを決めるだけで分布関数は計算できます。グラフに合わせるようにパラメータを調整するとかはナシです。
シーズン19について作成したグラフは以下。橙と緑の曲線が上述のモデルの分布関数、青がシーズン19のヒストグラムになっています。

なお、分布関数そのものではなくヒストグラムとの比較なのでヒストグラムのビン幅をモデルの分布関数にかけてます。
というわけで、次の計算式でレートの人口分布をかなりよく近似出来ることがわかりました
$$
f(x) = \begin{cases}
\frac{0.01N}{2} \times e^{0.01 (x-x_0) } & x < x_0\\
\frac{0.01N}{2} \times e^{-0.01 (x-x_0)} & x > x_0
\end{cases}\\
=\frac{0.01N}{2} \times e^{-0.01 |x-x_0|}
$$
