
レーティングの仕組みから見る「最終日」の重要性 part1:レーティングの定義と実際に使われている計算式
初めに
ぴらーん!いつも見てくれてる方はお久しぶり、初見さんは初めまして。最近さぼってたので久しぶりの投稿になります。
ほらそこ、いきなり痛い挨拶見て回れ右しない。
さて、本題ですがポケモンをやってるとランクマッチの最終日付近がやたらと重要視されてることに気づきます。対人ゲーは数あれどここまで終盤偏重なゲームはあまり出会ったことがない気がします。
今回はレーティングの観点から最終日の重要性を考察していきたいと思います。ポケモンSV想定ですが、Eloのレーティングを用いているゲームは多いので他のゲームでも参考になる部分はあるといいなと思います。
一記事じゃ全然収まらないのでシリーズものになりますが、長い目で見てもらえればと思います~。ちなみにpart1は事前調査とその解説になるので最終日うんぬんはまだありません。
1. 要約
ポケモンSVにおけるレーティングの計算式について計算式を検証し、Eloのレーティングを線形近似した簡易式が用いられていることを確認しました。
レーティングの計算式について、レートが定義できる条件や数値的に推定する方法などの面から解説をおこないました。
2. ポケモンSVにおけるレーティングの仕様
さて、シミュレーションによりレートの増え方を調べるにあたり、実際のゲームのレーティングがどのような計算式を使っているか調べる必要があります。
仲間大会では一戦ごとに少数点以下3桁までレートが表示されますし相手のレートがわかるためこれを記録して対戦前後のレート変化を調べることでレートの計算式を検証します。

使用するデータはテツポンドさんに提供いただいたデータと自分でもチョッッッッッットだけ集めてみたデータ併せて35戦分。
適当な計算式だと小数点以下まで合うことはなかなか続かないためこれだけのデータがあれば十分でしょう。
検証する候補の式としては次の2式について調査します。(a,bは対戦する二人のレート)
$$
{\frac{32}{1+10^{(b-a)/400}}}
$$
$$
16+0.04(b-a)
$$
これらの式はEloレーティングと言ってチェスなどにも用いられる有名な式です。
また、過去作のレーティングでも2番目の式が使われていたようです。[1]
式についての解説は後の章でおこないます。
これらの式を使って計算したレートの変化量と実際の対戦前後のレート変化を比較したのが次のシートになります。
シートを見ると上述のEloレーティングの式とレートの変化が合致しており、特に二つ目の簡易的な式の方で精度よくあっていることがわかります。
完全にぴったりあっているわけではないため、念のため誤差の程度を見積もっておきます。
相手のレートの小数点以下が不明なためレートの差(上式b-a)は0~0.999までの範囲の誤差を含みます。間をとって0.5の誤差があるとして対戦前後のレート変化にどれだけ影響があるかを見積もると0.04×0.5=0.02前後の誤差が出ることが予想できます。
実際、2つ目の式の理論値と実際のレート変化の差は0.02前後であり誤差の原因も特定できました。
まとめるとレートの増減に関して次の計算式が使われていることがわかりました。
$$
勝者の増加レート=16-0.04(勝者の対戦前レート-敗者の対戦前レート)\\
敗者の減少レート=-16+0.04(勝者の対戦前レート-敗者の対戦前レート)
$$
3. レーティングの計算式解説
さて、ゲーム内で使われている計算式がわかりましたが、この式はどこから出てくるのでしょうか?簡潔に解説していきます。
「レートとはそもそも何か?」と「どうやって計算するか?」は分けて考えた方が理解が深まると思っているので次のような流れで進めていきます。一般論としてそもそも強さを数字で表せるのはどういうときか?→さらに条件を追加してゲーム内で使われているレートを導出という流れで解説していきます。
3-1. 強さを数値化できる条件
そもそも一般的には一つの数字だけで強さを表すなんてことできないはずです。
まずはプレイヤーの強さを一つの数字だけで表せる条件について考えていきましょう。
一つの数字だけで強さを計ろうとするときにまず問題となるのは相性が存在するようなときです。グーはチョキに勝てるからチョキより強さの数字が大きい、パーはチョキに勝てるからもっと数字が大きい、みたいになってしまい強さをうまく定義できなくなります。
このようなケースを除外するために次のような推移律を導入して相性がない場合を考えてみましょう。
AさんがBさん強い、かつBさんがCさんより強いならばAさんがCさんより強い

このような関係があるとすると相性の問題はなくなりプレイヤーの強さを数値化しやすくなります。プレイヤーの強さを数値化するためには他にどのような問題があるでしょうか?
ちゃんと調べてみると実はそれ以上の条件は必要なく、上記の推移律だけの条件で強さを数値化できることがわかります。
具体的には基準となるプレイヤーを決めてそのプレイヤーに対する勝率を強さの指標として使えるようになります。
推移律がない時は基準のプレイヤーに対する勝率と目の前のプレイヤーに対する勝率がなんの関係性も持たないので強さの基準としては使えないのですが、推移律があることにより基準のプレイヤーにより高い勝率で勝てる人は基準以外のプレイヤーに勝ち越せる可能性も高いことがいえるようになります。つよい!!

ちなみにちゃんとした証明と主張もClaudeくん(AI)に書いてもらったので添付しておきます。
証明の中に出てくる文字は次のようなイメージで使っています。
$${x,y}$$:プレイヤー
$${w(x,y)}$$:xさんの勝率/yさんの勝率の比
3-2. レートからの勝率逆算
さて、前節で推移律があれば強さの指標が作れることは説明しました。
ところがこの指標、先ほどの条件だけだとどっちが強いかまではわかるのですが、どのくらい強いかまではわからないのです。
レートから勝率を逆算するためにはゲームの性質に合わせてさらに具体的な条件を設定していく必要があります。
脱線 -勝率とオッズ-
ちなみに脱線ですが計算するにあたってプレイヤーが別のプレイヤーに勝つ確率Wよりもその比であるオッズwを計算した方が便利がことがあります。
$$
オッズ=w=W/(1-W)
$$
1-Wは相手が勝つ確率ですので相手が勝つ確率と自分が勝つ確率の比をとったものになっています。
勝率とオッズは1対1に対応するので勝率が~%ですっていうのもオッズが○○ですっていうのもあまり変わらないのですが
以下この勝率を表すのにこのオッズを使っていきたいと思います。あまり変わらないので説明では勝率って言ってるかもですがオッズのこと指してます。
計算式の検証の際に出てきたEloレーティングの勝率①はこのオッズを使って書くと次のようにシンプルな式になります。
$$
勝率=W=\frac{1}{1+w}=\frac1{1+10^{\frac{(b-a)}{400}} }\\
オッズ=w=10^{\frac{(b-a)}{400}}
$$
シンプルに書けますね。
乗算的に推移するケース
話を戻して、単純なケースとして次のように積の形で定義される場合を考えましょう。
$$
w(x,z) = w(x,y) × w(y,z)
$$
ここで$${w(x,y)}$$はxさんの勝率とyさんの勝率の比、上で説明したオッズです。先に述べておくとポケモンの計算式はこの条件を仮定した結果として導出されます。
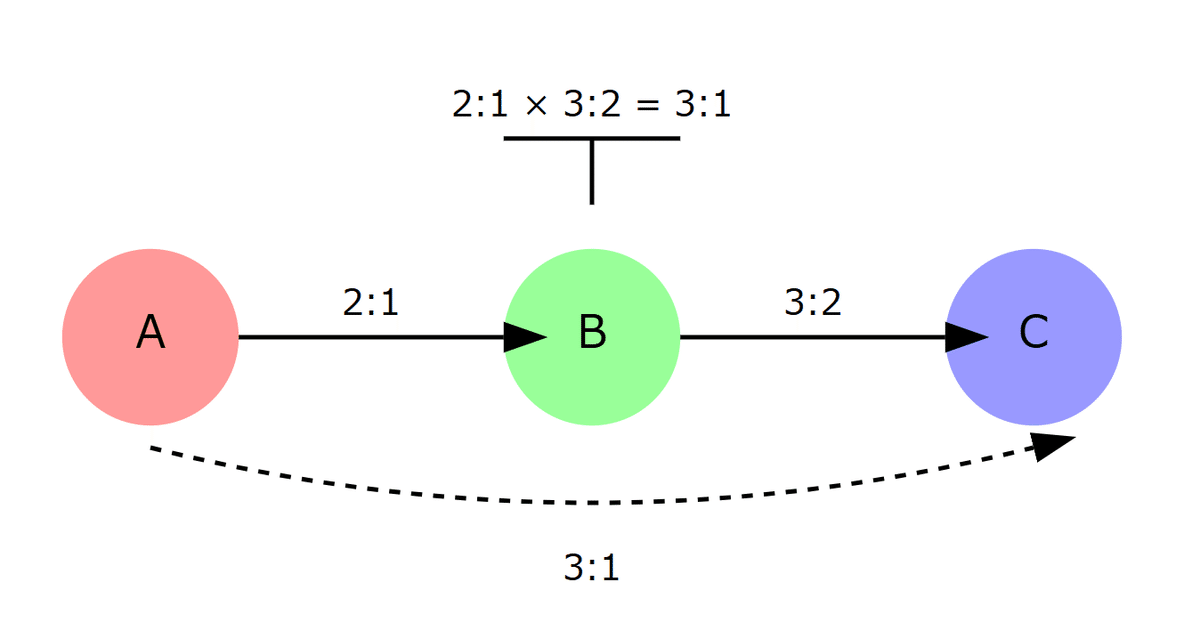
この場合、プレイヤーxとyの対戦の勝率は基準のプレイヤーpとの勝率を使って次のようにかけます
$$
w(x,y) = w(x,p) × w(p,y) = w(x,p)/w(y,p)
$$
wは変数を入れ替えるとどっちのプレイヤーが分母になるかが入れ替わるので逆数になります。
w(x,p)を強さの指標として採用することでxさんとyさんの勝率をそれぞれのプレイヤーの強さから計算することができます。
ちなみに強さの指標としてwを使ったので上のような式で勝率を計算しましたが、wを2倍したり定数足したり対数とったり指数とったりしても強さの指標として使えますし、適当に計算式を修正すれば勝率の計算もできます。せっかく強さの指標を定めるなら計算楽になるように定めたいですよね。wの対数を取ったものを強さの指標にすると強さの差を使って勝率を計算することができます。
強さの指標として次のRのように対数をとったものを使ってみましょう。このRのことをレートと呼ぶことにします。pは基準のプレイヤーとします。
$$
R(x)=400\log_{10}(w(x,p)) +1500
$$
重要なのは対数を取ることなので、400とか1500とかはあまり気にしなくていいです。
この時オッズwと勝率WそれぞれRを使って表すと次のようになります。
$$
w(x,y)=10^{\frac{R(x)-R(y)}{400}}\\
W=\frac{1}{1+10^{\frac{R(x)-R(y)}{400}}}
$$
したがって、レートから勝率への変換の公式をつくることができました。
この際ゲームの性質として$${w(x,y)×w(y,z)=w(x,z)}$$という条件を使いました。これらの関係が満たされなくなるとレートから勝率への変換ができなくなります。
レートの推定
さて、上までは互いの勝率が完全にわかっているという時に強さの指標を定義できるかという理論上のお話でした。
実際のゲームで強さを決めるには対戦結果から上で定めたレートを推定しなればなりません。
どうやって計算していけば対戦結果から推定できるでしょうか?
最もシンプルな方法として、「プレイヤーに推定用に仮のレートを与えておいて一戦ごとに変化させる。推定用のレートが正しいものになったらそのレートの変化量が0になるように計算式を工夫する」という方法が考えられます。
例えば勝率が$${50\%+(本当のレートの差)}$$で決まるようなゲームであればpを勝ったら1,負けたら0となる勝敗を表す量として
$$
レートの変化量=なんか定数×(p-50\%-推定用のレートの差)
$$
でレートを変化させ続ければ色んなレートをうろうろした末にレートの変化量の期待値が0になるところでレートの変化が落ち着きます。
そして、pの期待値が勝率になることを考えるとその「推定用のレートが最終的に落ち着く点」は本当のレートと同じ値になるのです。
上の例と違って勝率の式はもう少し複雑な式$${W(x,y)=\frac{1}{1+10^{\frac{R(x)-R(y)}{400}}}}$$を考えていますからそれを使って書くと次のようになります。ついでになんか定数のところもかっこ悪いのでKという文字に置きなおしておきましょう。
$$
Rの変化量=K(p-W(x,y))\\
=\begin{cases}\frac{K\times10^{\frac{R(x)-R(y)}{400}}}{1+10^{\frac{R(x)-R(y)}{400}}} & (勝った時)\\
-\frac{K}{1+10^{\frac{R(x)-R(y)}{400}}} &(負けた時)
\end{cases}
$$
このようにしてレートの推定を行うのをEloのレーティングといいます。最初に計算式を検証した時の候補の一つでもあります。
Kは32で使われることが多く、実際ポケモンでもK=32でもっとも計算式に合致します。
さらに線形近似といって複雑な関数を$${y=ax+b}$$のように一次関数で近似する手法があります。これとK=32を使って有効数字一桁で上記の式を近似すると次のようになります。
$$
Rの変化量
=\begin{cases} +16+0.04(R(y)-R(x)) (勝った時)\\
-16+0.04(R(y)-R(x)) (負けた時)
\end{cases}
$$
これは最初に調査したゲーム内で使われている式そのものです。
つまりポケモンのレートはEloのレーティングを線形近似で簡易的に計算したものだったのです!
もちろんこれは本当のレートに収束させる方法の一つでしかないので他にもより高度な方法は多数あります。
ただし注意しておきたいのはこの章は収束させる方法の一つでしかないため、あくまで収束先がどこになるかとかレートと勝率の変換公式というのは前の章、つまり$${ w(x,y)\times w(y,z)=w(x,z) }$$などの条件を決めた段階で決まってくるということです。
「もっと高度な方法あるのでポケモンのレートの決め方はダメ」みたいな悪口は収束の遅さには当てはまっても収束先のレートが変な数字になる部分に当てはまらない可能性があるので注意が必要です。
レートの説明まとめ
勝率に関して推移律があると強さの指標(=レート)が作れる
推移に関する具体的な関係式があるとレートから勝率の逆算ができる
特に勝率の比wに対して$${ w(x,y)\times w(y,z)=w(x,z)}$$という条件が満たされていると勝率は $${ W(x,y)= 1/(1+10^(R(x)-R(y)/400))}$$という式で表すことができる
一試合ごとにレートを変化させることでレートの推定を行うことができる。推定のための計算式はいろいろあり収束の速さ等も異なる。
4. 結論
今後シーズン後半のレート調査に入る際に重要な、「そもそも実際のゲームはどうなってんの?」という点について調査し、レートの計算式を検証しました。結果として過去作と同様次のようなEloレーティングの簡易式が使われていることがわかりました。
$$
勝者の増加レート=16-0.04(勝者の対戦前レート-敗者の対戦前レート)\\
敗者の減少レート=-16+0.04(勝者の対戦前レート-敗者の対戦前レート)
$$
また、レートが定義できる条件やレートから勝率を計算できる条件について計算・説明を行いました。これらについての理解は今後の調査を行う中で、計算式の修正・拡張を行う際に有用だと考えています。
5. 終わりに・次回予告
お疲れさまでしたー。長い記事ですが見てくれてありがとうございます。
シミュレーションに入る前の事前調査の内容を簡潔に書くつもりがあれも書きたいこれも書きたいで膨れ上がってしまいました。これで本命のシミュレーションがしょぼい結果になったら恥ずかしいですね///
前半の結果は過去作の資料が既にあるので2番煎じ感があるのは否めません。ただ、SVになって計算式が変わってる可能性も否定できないのでシリーズ変わるたびにこういう地道な検証は必要だと思っています。
後半のレーティング解説ではレーティングの定義の部分とそれを求めるための計算の部分で明確にわけてみたつもりです。いかがだったでしょうか?
ネットに落ちてるEloレーティングの解説は対戦によるレート変化の計算式でレートを定義していることが多く、それが定義なのか別のところから求められる計算式なのかがあいまいになりがちです。今後のシミュレーションの拡張のためにも理論上定義される「真のレート」と「現在の推定値」をわけて解説していく記事がたまにはあっても良いんじゃないかなと思って書きました。却ってわかりにくくなってたらゴメンナサイ。
次回はシミュレーションに入っていきます。まずはひねりのないEloレーティングで計算をおこない、終盤環境でレートが伸びやすくなるのかどうかといった部分を見ていきたいと思います!乞うご期待!!
6.参考文献
ポケモンデータまとめwiki https://w.atwiki.jp/poyon/pages/24.html#id_603403c9
フォロワーのテツポンドさんにはデータや画像の提供で多く協力いただきました。感謝!
