益川先生の業績のこと1: カイラル対称性の自発的破れに関わる研究

【概要】
先日亡くなられた益川先生の業績で、CP対称性以外の興味深い研究の紹介。1回目はカイラル対称性の自発的破れに関する研究。全2回の予定。

前置き： 「CP対称性の破れ」の研究

先日、益川敏英先生が亡くなられました。81歳でした。
2008年に協同研究者の小林誠先生と共にノーベル賞を受賞されています。

ノーベル賞の対象となったCP対称性の破れに関する論文

[1] Makoto Kobayashi and Toshihide Maskawa, “CP-Violation in the Renormalizable Theory of Weak Interaction,” Progress of Theoretical Physics 49 (2): 652–57, 1973.

はgoogle scholarで調べると引用数14000回を超えています。INSPIREという素粒子・原子核・宇宙関連の論文データベースによると、同分野の論文全体で2021年9月9日現在9番目の引用数です。理論分野に限れば（数値計算プログラムの使用法に関する論文も除く）引用数第3位です。1位はMaldacenaさんのAdS/CFT対応に関する論文、そして2位はやはり先日亡くなられたWeinbergさんの電弱統一理論に関する論文です。Ref.[1]ではWeinbergさんの作った電弱統一理論が重要な役割を果たすので、これを以降「Weinberg模型」と呼ぶことにします。

Ref.[1]はそれほど長いものではありません。全部で6ページです。また、フォーマットもゆったりしたものです。そして、ノーベル賞の対象となった「3世代以上のクォークの存在によるCP対称性の破れ」に関しては、最後6ページ目最上段から半ページに記述されています。該当部分は短いです。

この論文の基本的な結論は「CP対称性はその当時までに見つかっていた粒子から構成される、Weinberg模型に基づいたまともな理論（=実験と無矛盾な理論）では破れようがない」というものです。CP対称性は粒子と反粒子の"同じさ"に関わるもので、CP対称性が完全に成り立っていれば、粒子と反粒子の性質が同じであると言えます。実験的にはこの対称性が破れていることは、1964年のCroninらの実験でわかっていました:

[2] J. H. Christenson, J. W. Cronin, V. L. Fitch, and R. Turlay. 1964. “Evidence for the $${\pi}$$ Decay of the $${K^{20}}$$ Meson.” Physical Review Letters 13 (4): 138–40.

このような背景のもと、Weinberg模型に基づきどのようにそれを拡張したらCP対称性が破れうるかを小林・益川両先生は考えました。そして上記の結論を得ました。

Ref.[1]が素晴らしいのは、それにとどまらず、ではどう理論を拡張したらCP対称性が破れうるかを考察したことです。まず未知の（擬）スカラー場を導入すると破れうることに言及しています。そして次に、ノーベル賞の受賞理由となるアイディアを提示しています。その主張は、未知のクォークが存在すれば、しかも第３世代目というそれまでに（たぶん）予言もされていないクォークが存在すればCP対称性が破れうるというものです。クォークは素粒子の一種で、当時u、d、sクォークという粒子が存在していることは実験でわかっていました。また、未知のクォークであるcクォークというのがあることは「フレーバーを破るニュートラルカレント（FCNC）の抑制」という実験事実から示唆されていました。しかし小林・益川が予言したクォークはudcsのどれでもなく、さらにもう2つ（以上）の別のクォークです。彼らはそのようなクォークが存在すれば、ラグランジアンに現れる場の係数に虚部が現れ、CP対称性が破れうることを示しました（クォークが3世代以上あると、クォークの位相変換の自由度ではラグランジアンの虚部を消すことができなくなることにより示される）。

この論文は1972年にProgress of Theoretical Physicsという日本の雑誌に掲載されたのですが、このあたりの年が素粒子物理の激動の時代であり、混沌としていた素粒子の理論の中で、ゲージ理論が一躍主役に躍り出た時期でした。電弱統一理論のくりこみ可能性が証明されたのが1972年、ポリッツァー、グロス・ウィルチェックさんらが量子色力学が漸近的自由であることを証明したのが1973年なので、まだ混沌の時期だと思います（以前の記事"すごい人：トホーフト" 

をご参照ください）。どの模型が正しいか完全にはわかっていない状況で、くりこみ可能な模型に関してCP対称性の破れの可能性を探り、そしてそこで提案されたモデルが現実の世界で実現されていたというのは、驚異的に思えます。ちなみに、本論文ではいくつかのCP対称性の破れの可能性を議論していますが、３世代クォークによる破れの議論が最終ページの冒頭から改めて始まっていることから察するに、やはりこの可能性がいちばん重要だと思っていたのだと思います。

他にもある、益川先生の興味深い重要な研究

上記のCP対称性の破れはいわゆる弱い相互作用に関することです。これに対し、強い相互作用という別の力に関連した研究も益川先生はされています。この記事では、益川先生の強い相互作用に関する研究に関して述べたいと思います。

先生が関わられた研究の題目をあげると

・クォークの質量の起源
・$${\eta}$$-$${\eta’}$$ mixingに関する研究
・Gribov問題に関すること
・SUSYの非線形表現に関する研究
・原子核のcollective coordinateに関わる研究
・格子QCDによるテクニカラーに関する研究
...

などがあります。これ以外にもきっとあると思いますがご容赦ください。

強い相互作用には非常に重要な２つの側面「カイラル対称性の自発的破れ」「カラー閉じ込め」がありますが、これらに関わる
・クォークの質量の起源（と$${\eta}$$-$${\eta’}$$ mixingの話もちょっとだけ）
・Gribov問題に関すること
に関して紹介したいと思います。この記事では「クォークの質量の起源に関わる研究」を紹介し、次の記事で「Gribov問題に関すること」を紹介します。これらは益川先生と、宇都宮大学で教鞭を執られた中島日出雄先生（残念ながら中島先生もお亡くなりになっています）お二人の研究です。

ひとつ言っておくべきことがあります。多くの分野では最もcontributionが高い人が論文の最初に名前を乗せるfirst author制度をとっているのではないでしょうか。しかし素粒子分野は基本的にはfirst author制ではありません。名前はアルファベット順になっていることが多いと思います。これは、素粒子分野では、研究に関わった人は皆、役割は違えどequal contributionをするべきという理念があり、逆にそうでない人はそもそも論文に名前が載るべきではないという精神を表しているのだと思います。あとリベラルな思想とも関わっている気がします。何が言いたいのかというと、この論文はMaskawa, Nakajimaという順で名前が載っているので益川先生がfirst authorに見えますが、たぶんそうではなく、equal contributionだということです。ただ、益川先生が英語が苦手というのは有名な話なので、論文の英語作成に関しては中島先生が行ったのかもしれません笑

物質の質量の起源にかかわる研究

ここから以下の論文

[3] Maskawa Toshihide and Hideo Nakajima, “Spontaneous Breaking of Chiral Symmetry in a Vector-Gluon Model,” Progress of Theoretical Physics 52 (4), 1326–54., 1974; “Spontaneous Breaking of Chiral Symmetry in a Vector-Gluon Model. II,” Progress of Theoretical Physics 54 (3), 860–77, 1975.

を紹介したいと思います。ちなみに論文での益川先生の名前の綴りはMasukawaではなくMaskawaなのでご注意ください。

小林先生・益川先生は、南部陽一郎先生と共にノーベル賞を受賞されました。南部先生は「対称性の自発的破れ」に関する研究が受賞理由ですが、ここで紹介する益川先生の業績は、まさにこの「対称性の自発的破れ」に関する研究です。

2種類のクォーク質量

クォークは陽子・中性子の構成粒子です。陽子・中性子はu,dクォークという2種類のクォークからできています。

ここでu, dクォークの質量を調べてみましょう。Particle Data Group(2019年版)では、それらの質量の中心値はuクォーク2.16MeV、dクォーク4.67MeVです（最後の[注]参照）。次に陽子の重さを調べてみましょう。googleで"proton mass"と入れると一番上にデーンと表示されます（SI単位系なのでキログラム表示ですが）。これはだいたい938MeVです。938MeVはuクォークの質量の400倍、dクォークの200倍くらいなので、陽子はおおざっぱに200コから400コくらいのu, dクォークでできているように思えます。

しかしWikipedia等調べてみればわかりますが、陽子はuクォーク2つ、dクォーク1つからできていると書かれています。この食い違いはなんでしょうか。

「クォーク」「クォークの質量」というとき、実は２種類あります。強い相互作用の基礎理論であるQCDのラグランジアン（=粒子間の相互作用を決定する関数）に現れる質量を「裸の質量」とか「カレントクォーク質量」とよび、これをもつクォークを「カレントクォーク」といいます。この質量が前述のu, dクォークの質量です。一方で「構成子クォーク」「構成子クォーク質量」という概念が存在し、これはクォークが強い相互作用に現れるグルーオンという粒子の衣を纏い、カレントクォーク質量より重くなったものを指します。この質量がu,dともに938MeV/3〜300MeVくらいになるので、陽子の重さが説明できます。

ちょっと脱線ですが、世の中よく言われる「素粒子の質量はヒッグス粒子によりもたらされる」と言うのは正確ではありません。地球の質量は、原子核の重さ、すなわち陽子・中性子の重さが大半を占めています。カレントクォーク質量はヒッグス粒子によりもたらされます。しかし上述のとおり、それは陽子の質量のわずかな部分にしか寄与しません。実質グルーオンの衣、すなわち強い相互作用こそが地球の質量を担っているのです（※ややこしいのですが、宇宙全体の質量となるとダークマターが大部分を占めるのでまた異なります）。このようなグルーオンによる質量の獲得はヒッグス機構になぞらえ"dynamical Higgs phenomenon"と呼ばれることがありますが、決していわゆるヒッグス粒子によるものではありません。

しかしこの「構成子クォーク質量」、実際にQCDからその質量を計算してみろと言われると至難の技です。なぜかというと、詳しいことは省きますが、陽子内部ではクォークとグルーオンが非常に強く相互作用しあっていて、QCDから直接物理量を計算する"正当な"方法である摂動論が使えないためです。いまでこそ格子ゲージ理論・格子QCDと呼ばれる、QCDの数値計算手法により、このグルーオンの衣の質量を評価することができますが、1974年当時にはそんな方法は存在しませんでした[注2]。

この構成子クォーク質量生成のメカニズムに関して研究したのが上記の論文
です。これらはCPの破れの論文と比較して非常に長い論文です。IとIIがあり、どちらも28ページ程度です。またRef.[1]は式は多くなく、数学的には代数学の議論が主ですが、こちらは解析学バリバリで式も大変多く、かつ物理にしては珍しく定理と証明の連続で、数学の色が濃いです。

この論文では、vector gluon modelという、くりこみ（=量子場の理論に現れる発散を系統的に除去する操作）が可能なモデルを用い、クォークが伝播する間にグルーオンが無限に交換されることでクォーク質量が得られることを証明しています。その際重要なのは、カイラル対称性をこわさないような近似を使うことです。そしてそのような近似のもと得られた、クォークの質量に関する積分方程式の解に関して詳しく議論しています。

カイラル対称性の自発的破れと構成子クォーク質量の関係

論文のタイトルをみると"Spontaneous Breaking of Chiral Symmetry"とあります。日本語にすれば「カイラル対称性の自発的破れ」。これは素粒子の質量生成に大変重要な概念なので、以下に概要を記します。

クォークのようなフェルミオンと呼ばれる粒子には「巻き方」の概念が存在し、右巻きと左巻きの粒子が存在することが可能です。そして粒子に質量がないとき、右巻き粒子と左巻き粒子が独立して存在します。そしてこのとき「カイラル対称性」と呼ばれる対称性が存在しています。逆に言えば、フェルミオンに粒子が存在する時、左右の巻き方の粒子は独立には存在せず（正確にはディラックフェルミオンに対してこれが成り立つ）、カイラル対称性は破れています。この対称性は裸のクォーク質量が存在するため正確に言えば完全にはなりたってませんが、裸のクォーク質量がハドロンの典型的な質量より十分小さいことにより、強い相互作用では近似的に成立しています。

しかしこの対称性が成立している量子場の状態は不安定です。わずかな裸の質量の存在により、対称性が破れた状態で落ち着きます。これを対称性の自発的破れといいます。ちょうど山のてっぺんにボールを置くようなものです。左右にちょっとでもずれれば、どちらかのスロープに落ちていきます。この現象には次のような違うアナロジーがあります（例えば南部陽一郎先生の名著「クォーク」（ブルーバックスシリーズ）にこの説明があります）。

[図1] テーブルにならんだナイフとフォークのセットの図。焦げ茶の小さい円は人の配置を表し、白い長方形はナイフ・フォークセットを表す。

上の図をみてください。レストランで複数の人が円形のテーブルにつき、豪華な夕食を食べようとしています。テーブルに人数分ナプキンに巻かれたナイフとフォークのセットがあるのですが、どの椅子からみてもちょうど左右均等に配置されているため、自分の右と左のセット、どちらを使えばよいかわかりません。しかしある人が自分の使うナイフ・フォークのセットを決定した瞬間、他の人の使うものも決定されます。もともと左右どちらも対称であったけど、たったひとりの小さな行動が、全員のつかうセットを決定し、結果ディナーを食べる行動は左右の対称性を壊しています。100人いようが1000人いようが1人の行動で壊れてしまいます。

このような現象が対称性の自発的破れです。量子場の理論の言葉と対応させると次のようになります。もともとカイラル対称性は存在しているのだけど、力学的なセットアップにより、実際に実現される状態においてカイラル対称性が成立すると不安定な状態になり（↔ナイフ・フォークセットが椅子の真ん前に存在せず左右に均等に配置されているが、食事をするためには必ずどちらかを選ばなければならない）、結果量子場の状態（↔テーブルの人々がディナーを食べている状態）は何らかのちょっとしたきっかけで（↔だれかが最初にどちらのセットを使うかを決めることで）カイラル対称性を破ってしまう（↔左右の対称性を破ってしまう）のです。そして、「上記したこと=カイラル対称性が成立していると質量が存在しない」の裏返しで、カイラル対称性が自発的に破れることで質量が生まれます。

しかしここで、もともと対称性が存在していたことの名残が生じます。それが「南部・ゴールドストンモード(NGモード)」です。先程の例におけるアナロジーをつかうと、すでにディナーを食べ始めたのち、だれかがそれまで使っているものと逆側のナイフ・フォークを誤って使うと、そのとなりの人も逆側のナイフを使い出し、その隣の人も逆側のナイフを使い出し...と影響が続々と伝わるような動き（=モード）が生じます。この影響は波のようにつたわっていきますが、これが量子場の理論では粒子として現れます(本当は連続的な対称性でしか起きません。あくまでアナロジーなのでご容赦ください)。これを「南部・ゴールドストン粒子(NG粒子)」と言います。このモードの「波長」はいくらでも長くなれます。あるひとの逆側のナイフ・フォークを使う影響は、場合によっては皆ほとんどいっしょにとなりのナイフ・フォークを使うでしょう。このような状態は「波長が長い」状態で、このようなモードを作りだすのに、量子場の理論では無限に小さいエネルギーですみます。相対論ではエネルギーは質量と等価であり、この事実は質量がゼロのNG粒子をもたらします。そしてNG粒子は現実に存在します。もっとも有名なNG粒子はπ中間子・パイオンと呼ばれる粒子です。パイオンは中性子・陽子同士を結合する媒介役になっています。強い相互作用の到達距離から、パイオンの存在と質量を湯川秀樹先生が予言したのは有名です。強い相互作用は、非常にミクロな目で見ればクォークとグルーオンの相互作用の結果です。しかし、もっと引いた視点=粗視化した視点からすると、強い相互作用の世界は、中性子・陽子とそれらを結合させるパイオンからなっています。

まとめると
・カレントクォークはカイラル対称性の自発的破れの為構成子クォーク質量を得る。
・その結果質量ゼロのNG粒子が現れる
ことになります。

益川・中島論文でやったこと

さて、ではQCDからどうやってカイラル対称性が破れ、そしてNGモードが生じるのでしょうか。上記したように強結合のQCDにおいてこれを調べるのは容易ではありません。この問題に、vector-gluon modelというくりこみ可能な模型において、クォークとグルーオンのダイナミクスにある近似を施し、Schwinger-Dyson方程式というものを立ててその解を考察することで挑んだのが益川・中島の上記の論文です。

vector gluon modelにおけるSchwinger-Dyson方程式と呼ばれる方程式は、以下のような自己無撞着方程式です：

詳細は省きますが、グルグルと巻いた線がグルーオンの伝播関数D_{μν}を表しています。伝播関数とはどのくらいの確率で粒子が伝播するかを表す関数のことです。ここで用いているグルーオンの伝播関数は相互作用の効果を含まない伝播関数です。ただしゲージ固定関数およびグルーオンの質量項を含みます（ゲージ固定に関しては詳しいことは省きますが、次の記事で説明する予定です）。直線で表した$${S}$$がクォークの伝播関数です。$${\Sigma}$$は自己エネルギーと呼ばれる量です。$${\gamma_\mu, \gamma_\nu}$$はガンマ行列と呼ばれるもので、これに関しては「裸の頂点=なんの相互作用も含まない頂点」を採用しています。$${S }$$と$${\Sigma }$$が定まります。

さて、形式的な議論で、この方程式の解としての$${S}$$がどのようなダイアグラムなるかを考察しましょう。下記の図の一番上のダイアグラムのように、初期のiSを、直線にバツがついているもの（$${iS=}$$の式の右辺第一項）にして、上記の式により逐次的に$${\Sigma}$$と$${S}$$を構成していきます。すると

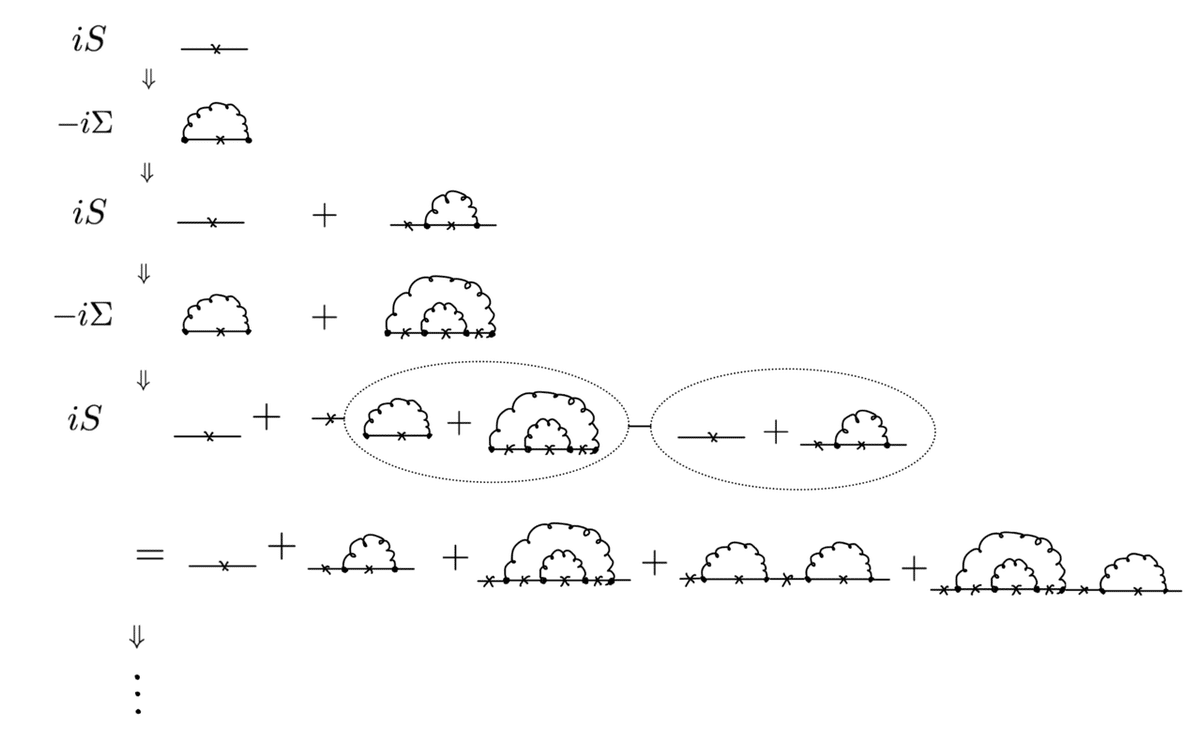
のようになります。詳細はともかく、クォークを表す線にどんどんグルーオンが追加されていくことがわかると思います。このようにこの方程式の解は、まさにクォークがグルーオンの衣を着るという描像を実現します。ただし気をつけてほしいのは、このような逐次的な過程を繰り返して解を求めるのではなく、実際にはこの方程式を完全に満たす解＝自己無撞着な解を求めます。そしてこのような方程式の解は摂動的に求める（=結合定数の展開をどこかで止めて求める）ことはできません。この解は無限次の結合定数の影響を含んでいることが重要です。実は対称性の自発的破れは摂動的には起こらず、必ずこのような非摂動論的な扱いが必要です。

そして実は、クォークの伝播関数にこのような近似を施すこととNGモードには関係があります。益川・中島は、このようなグルーオンのレインボーダイアグラム（上のグラフが虹のように見えるのでこう呼ばれる）の足し上げがカイラル対称性を尊重する（＝カイラル対称性が成立する）ことを、軸性カレント$${j_p}$$と軸性ベクトルカレントに$${j^5_\mu}$$に対するWard-Takahashi恒等式

が成立することを確かめ、そのうえで解を考察しています。

実はグルーオンダイアグラムの足し上げによってNGモードを記述することができます。Bethe-Salpeter方程式という自己無撞着方程式により、クォーク・反クォークの間にグルーオンが無限に飛ぶダイアグラムを足し上げたものがこのNGモードになります。Schwinger-Dyson方程式とBethe-Salpeter方程式は密接に関係しています。上記した軸性（ベクトル）カレントに関するWard-Takahashi方程式が成立していないと、クォーク・反クォークの束縛状態として生じるパイオンのような中間子=NGモードが、裸のクォーク質量がゼロの極限でゼロになる保証がありません。つまり、NGモードが軽くなることにWard-Takahashi方程式が重要であり、これが成立するような近似を用いることは、強い相互作用の模型を作る上で重要な指針となります。

ここでひとつ注意しておきます。上のほうで、カイラル対称性が破れるから質量が生じると書きました。そしていま陽子などを記述する際にはクォークは質量をもってほしいのです。ならカイラル対称性を尊重する必要などないではないか、と思うかもしれません。しかし、ここで言っているカイラル対称性の尊重というのは、カイラル対称性があからさまには破れないことを意味します。上記の会食におけるテーブルの例で言えば、カイラル対称性を尊重しているというのは、フォーク・ナイフセットが椅子の前に左右対称におかれている状況に対応します。そして、パイオンのようなNGモードの存在を保証しながら質量を生成するには、カイラル対称性が自発的に破れることが重要です。テーブルの例で言えば、誰か1人がどちらかのナイフ・フォークセットを取ることで、全員のセットがどちらか決定されなければなりません。

vector-gluon modelのよい点は、上述のようにクォークがグルーオンの衣を着て構成子クォーク質量を獲得するという描像を実現していると共に、カイラル対称性を尊重する近似を用いればNGモードがちゃんと軽くなることも実現している点です。

ちなみに、この論文のイントロダクションには、vector gluon modelの利点がもうひとつ示されています。実験的には、NG粒子と考えられる粒子はパイオンのほかに7つ、計８つあります。ところが、理論的な対称性の議論からは、NG粒子は9つなければならず1つ足りませんでした。$${\eta’}$$という粒子が本当はもっと軽くNG粒子になってほしいのに、実際にはNG粒子とみなせないくらいに重いのです。これは$${{\rm U}_A}$$(1)問題と呼ばれ大問題だったのですが、最終的に「$${{\rm U}_A }$$(1)対称性の量子異常による破れ」という機構により、$${\eta’}$$だけ重い理由が理解されました。そして$${\eta’}$$が重くなる機構がvector-gluon modelには自然に備わっているのです。ちょっとむずかしいのですが、vector-gluon modelでは原理的にはAdler-Bardeen anomalyという量子異常をもたらすダイアグラムが存在し（この論文の取扱いではそのようなダイアグラムは入りませんが）、そのため$${\eta’}$$が重くなる機構が自然に実現しています。一方で、NJL模型という、やはり自発的対称性の破れを実現する模型では、6クォーク頂点という当時としては出所不明の相互作用を特別に導入しないと、$${\eta’}$$だけ重い理由を説明できませんでした。

少し脱線なのですが、実は、小林・益川は1970年にProgress of Theoretical Physicsの"Letters to the Editors"において"Chiral Symmetry and $${\eta}$$-X Mixing"という論文を書いています。この論文では $${\eta’}$$の質量が6クォーク頂点相互作用の導入により重くなることを実現できることを示しています。これも小林・益川の大変重要な研究です。ただし、上に述べたように、その存在理由はわからず、とにかくそれを導入することで$${\eta’}$$の質量が説明できることを論文では述べています。そしてその後トホーフトという研究者により、このような相互作用が非可換ゲージ場の理論のトポロジカルな配位であるインスタントン（当時はpseudoparticleと呼ばれていました）によりもたらされることが1976年にわかりました:

[4] Gerard ’t Hooft, 1976. “Computation of the Quantum Effects due to a Four-Dimensional Pseudoparticle.” Physical Review D: Particles and Fields 14 (12): 3432–50. ; “Erratum: Computation of the Quantum Effects due to a Four-Dimensional Pseudoparticle.” Physical Review D: Particles and Fields 18 (6): 2199–2200.

この仕事により、NJL模型に6クォーク頂点相互作用を入れることにQCDの理論的なバックグラウンドができ、正当化されました。そしてこの相互作用には"Kobayashi-Maskawa-'t Hooft interaction"という名前がついています。3人ともノーベル賞受賞者というのはなかなかすごいですね。

ひたすら解の存在を数学的に考察する

上記の方程式の解は、自発的に対称性が破れたものとそうでないものが存在し得ます。そこで、どのようなときに対称性の破れた解が存在するかを調べています。この論文が長いのは、方程式が複雑なため、これを解析するのに、方程式に存在するパラメータで場合分けをして解析しているのがひとつの原因です。裸のクォーク質量$${m_0}$$がゼロか否か、結合定数が大きいか否か、またゲージ固定関数というものがあるのですが、これに関する場合分け等がなされています。そしてそれぞれの場合に関数方程式の解の存在・一意性を数学的に厳密に議論しています。その際不動点定理

[定理1]
Banach空間において、コンパクトで閉じた凸集合における自分自身への連続写像は、少なくともひとつの不動点をもつ

[定理2]
Banach空間において、境界を持つ閉じた集合における自分自身への連続写像$${\psi}$$が厳密な意味で縮小写像であるとき、すなわち、集合の任意の2点$${α_1}$$と$${α_2}$$に対し、以下の条件

を満たす$${α_1}$$と$${α_2}$$に依存しない定数kが存在するとき、この写像にはただ1つの不動点が存在する

を用いています。不動点とは

のことです。
この定理における「点」は、それがこの定理における条件を満たすなら、通常の点だけでなく写像（関数）でもいいです。そしてこの論文では、関数空間における「点」に関してこの定理を利用することで、関数方程式の解の存在、一意性を議論しています。数学屋さんは非常に便利な定理を用意してくれているものです。この論文では、ゲージ関数、裸のクォーク質量、結合定数の様々なケースで解の存在を数学的に議論しています。

当時数値計算はできた？

またまたちょっと脱線。

今ならこのような方程式の解に関する論文では、方程式の解析のため、必ず数値計算をするといってよいです。実際、1980年代以降のこの系統の研究論文では、だいたい数値計算が載っています。しかし本論文には数値計算はありません。本論文は1974年出版ですが、所属先の京都大学では1969年よりFACOM230-60という汎用コンピュータが導入されています（1974年よりFACOM 230-75（1CPU, 512KW, 5MIPS）が導入されてはいますが、1974年3月2日に受理された論文でこれを使用することはできないでしょう）。計算能力は0.8MIPSです。対して、現在家庭用パソコンで普及しているCPUの計算能力は300,000MIPSを超えるものも珍しくありません。今や上記の方程式を解くコードは例えばPythonで簡単に作成できます。実際解いてみると、うまく書けばPythonだと0.4秒程度で信頼のおける解が求まります。Fortranだとgfortranに-O2オプションをつけて0.03秒程度でした。もし当時FACOM230-60を使って数値計算を行っていたとしたら、1つのパラメータセットに対し解を得るのに6時間から10時間程度かかるのではないかと思います。解を考察するには、さまざまなパラメータセットに対して計算を行わなければならないので、ひととおり解を調べるには少なくともパラメータ50セット分くらいの計算はしなければならないのではないでしょうか。しかしコンピュータは共用なので自分だけが使うわけにもいきません。ミスもするでしょう。そもそもまだまだ数値計算は当時それほど行われてなかったので、コードを書くのも一苦労でしょう。さらに当時はパンチカードによる記述であり、かつ遠隔でコードを動かすこともできないため、苦労はひとしおです。数値計算ではなく、厳密な数学的考察を行ったのもうなずけます。

論文の主要な結論

さて、この論文の結論に関して。主な結論として

「自発的に対称性が破れ、クォークが構成子クォーク質量をもつような解が、弱い結合領域ではなく強結合領域に存在する」

ということを示しました。強結合領域にそのような解が存在することは大変重要です。その重要性は、「QCDは漸近的自由性という著しい性質を持つ」ことに由来します。

1960年代の終わりに、ビョルケン・スケーリングという強い相互作用の"意外な"性質がみつかりました。これは、非常に高いエネルギーの仮想光子を使って陽子内部を見ると（顕微鏡で中を見るようなものです）、ほとんど自由に動く粒子"パートン"が存在することがわかりました。これは強い相互作用を記述する理論が、高エネルギーでは相互作用が弱くなることを意味しています。逆に言えば、低エネルギーでは相互作用が強くなるということです。このような性質を「漸近的自由性」と呼びます。いまから考えれば、これはまさにQCDが強い相互作用の理論であることの証左だったのですが、実は漸近的自由性を持つ理論はなかなか見つけることができなくて、一時は「漸近的自由性をもつ理論は作れない」という定理ができたほどです。もちろんこれは間違っており、ポリッツァー・グロス・ウィルチェックさんらによるQCDの漸近的自由性の発見により、QCD=強い相互作用の基礎理論であることが強く示唆されました。

本論文で示された結果は、漸近的自由性と関係しています。カイラル対称性が破れた解が、この世界、すなわち低エネルギーの世界に存在することを示しました。この研究は、クォーク・グルーオンからなる理論において、うまい近似を入れグルーオンのレインボーダイアグラムを足し上げれば、実験で観測されている現象と無矛盾な形でカイラル対称性が自発的に破れうるという重要な結果を、数学的に厳密に示しています。

ただ、この結果はいくつかのQCDにはない仮定に基づいています。たとえば、この論文では運動量に人為的なカットオフを入れて計算を行っています。その後、そのようなカットオフなしに、漸近的自由性をQCDの走る結合定数の形でSD方程式に反映させることで、対称性が自発的に破れた解を構成した研究（東島、Miransky、'83）が現れました。これは益川・中島より更にQCDに忠実に基づいた模型と言えると思います。このようなSD方程式、また2体のクォークの束縛状態（=中間子、メソン）に関するBethe-Salpeter方程式は、現在でも有力な研究手法として使われています。

そして現在では、上記したように、格子QCDという数値計算により、強い相互作用の多くの実験事実がQCDから説明できるようになっています。いまやQCDが強い相互作用の基礎理論であることは殆ど疑いようがありません。

こんなところで本論文の解説は終わりにします。

次回予告

閉じ込めに関わる可能性が指摘されているGribov問題のお話を、益川・中島両先生の以下の２つの論文

Toshihide Maskawa and Hideo Nakajima. 1978. “How Dense Are the Coulomb Gauge Fixing Degeneracies? Geometrical Formulation of the Coulomb Gauge.” Progress of Theoretical Physics 60 (5): 1526–39.

Toshihide Maskawa and H. Nakajima. 1980. “Structure of the Gauge Transformation Group in the Square Integrable Space and Gribov’s Ambiguity in the Coulomb Gauge.” Progress of Theoretical Physics 63 (2): 641–55.

を通して紹介したいと思います。

おしまい

[注] MeVはメガ(M)エレクトロンボルト(eV)の略。eVは電子1つを1ボルトの電位差で加速したときに電子が得るエネルギーです。そしてここでは自然単位系というのを使っています。この単位系は、光速$${c}$$およびプランク定数を$${2\pi}$$で割った換算プランク定数$${ħ}$$を1とすることで、すべての単位を質量・時間・距離のいづれか1つの単位のべきで表すものです。クォークの質量はもちろんエネルギーではなく質量の単位をもつのですが、この単位系では、MeVを$${c}$$と$${ħ}$$のべきを適切にかけることにより質量の単位にします。MeVを質量にするにはMeV/$${c^2}$$とすればいいです（これは有名な$${E=mc^2}$$をつかってエネルギーを質量に換算するのと同じ）。よって

$$
\begin{align*}
1{\rm MeV}（自然単位系において質量の単位）&=1{\rm MeV}/c^2\\
&\simeq 1.78\times 10^{-30}{\rm kg}
\end{align*}
$$

になります。

[注2] ちょうどRef.[3]が出版された年、K.G.Wilsonが格子ゲージ理論のアイディアを発表しています。