メタアナリシス:リスク差評価には、モデリングと二変量ランダム効果モデルが望ましい
方法3(モデリング)と方法4(二変量ランダム効果モデル)のRプログラムソース:
GitHub - linlf/RD: Methods for estimating absolute risk reduction derived from meta-analyses of binary outcomes

Murad, M Hassan, Zhen Wang, Ye Zhu, Samer Saadi, Haitao Chu, and Lifeng Lin. “Methods for Deriving Risk Difference (Absolute Risk Reduction) from a Meta-Analysis.” BMJ, May 5, 2023, e073141. https://doi.org/10.1136/bmj-2022-073141.
まとめポイント
絶対的なリスク低減やリスク差は意思決定のための重要な指標である。しかし、リスク差を推定するための利用可能な方法には限界がある
複数の研究から生成されたリスク差のメタアナリシスにおけるプーリングは、ベースラインリスクの違いによるリスク差の変動によって制限される
プールされた相対効果(リスク比やオッズ比など)をリスク差に変換する方法は、最も一般的に使用され推奨されている。しかし、この方法ではベースラインリスクの不確実性が考慮されていないため、逆に高リスク集団ではリスク差推定値が不正確になり、低リスク集団では正確になる。
モデリングは、試験による相対的効果と観察研究によるベースラインリスクを組み入れることができ、両方の不確実性を考慮することができるため、ベースラインリスクの不確実性に関する情報がある場合には、好ましいアプローチである
二変量ランダム効果モデルは、ベースラインリスクに基づく条件付効果を計算するもので、十分な研究が利用できる場合には好ましい。
Translated with DeepL
要約:ベネフィットとハームをトレードオフするためには、絶対的なリスク低減やリスク差の知識が必要であり、リスク差は意思決定において重要な指標となる。リスク差の信頼区間は、ガイドライン作成者が行う不正確さ判断の基礎となる。しかし、リスク差の推定は簡単ではなく、利用可能な方法には様々な限界がある。本稿では、4つの方法について議論する。1つ目の方法は、複数の研究から得られたリスク差をメタアナリシスでプールする方法であるが、ベースラインリスクの違いによるリスク差の一貫性のなさが大きな限界である。第二の方法は、プールされた相対効果(リスク比やオッズ比など)をリスク差に変換する方法であるが、その信頼区間にはベースラインリスクの不確実性が組み込まれていないことが大きな限界である。この信頼区間は、ベースラインリスクが増加するにつれて直線的に広がり、高リスク集団のリスク差推定を不正確にし、ベースラインリスクが低い場合には、誤解を招くほど正確なリスク差につながる可能性があります。2つの代替法により、これらの制限を軽減することができる。単純なマイクロシミュレーションアプローチは、相対効果とベースラインリスクの両方における不確実性をモデル化することができる。二変量ランダム効果モデルは、治療群と対照群のリスクを共同で分析し、ベースラインリスクに基づく条件付効果を計算する。これら4つの方法をケーススタディに適用し、各アプローチをどのような場合に使用するかについての推奨事項を示す。また、メタ分析者やガイドライン作成者によるリスク差の推定を容易にするための実践的なアドバイスとオープンソースのRコーディングを提供します。
Translated with DeepL
重要性とリスク差のトレードオフの他に、リスク差の信頼区間は推定値の確実性と決定の確実性に関する判断の基礎となります。GRADEアプローチに従って、リスク差の信頼区間が意思決定の閾値を超えない場合、治療効果は正確(つまり、より確実)と見なされます。リスク差は対象population基準リスクに基づいて変化するため、この精度の判断は、関心のある結果の異なる基本リスクを持つ対象populationに対して別々に行う必要があるかもしれません。 したがって、特定の基本リスクを持つ患者グループに対応するリスク差と関連する信頼区間を推定するための堅牢な方法が必要です。
単一の研究からリスク差を推定することは簡単です。個々の研究で各グループのリスクを計算するだけです。リスク差は、2つのグループのリスクの差として計算され、その標準誤差と信頼区間もリスクとサンプルサイズを使用して導出することができます。ただし、実際のところ、問題のトピックに関して複数の研究が発表されていることが一般的です。複数の研究からリスク差を推定することは簡単ではなく、利用可能な方法にはいくつかの制限があります。
この文では、メタアナリシスからリスク差を推定するための4つの方法を説明します。
第1の方法は、個々の研究から得られたリスク差のメタアナリシスです。
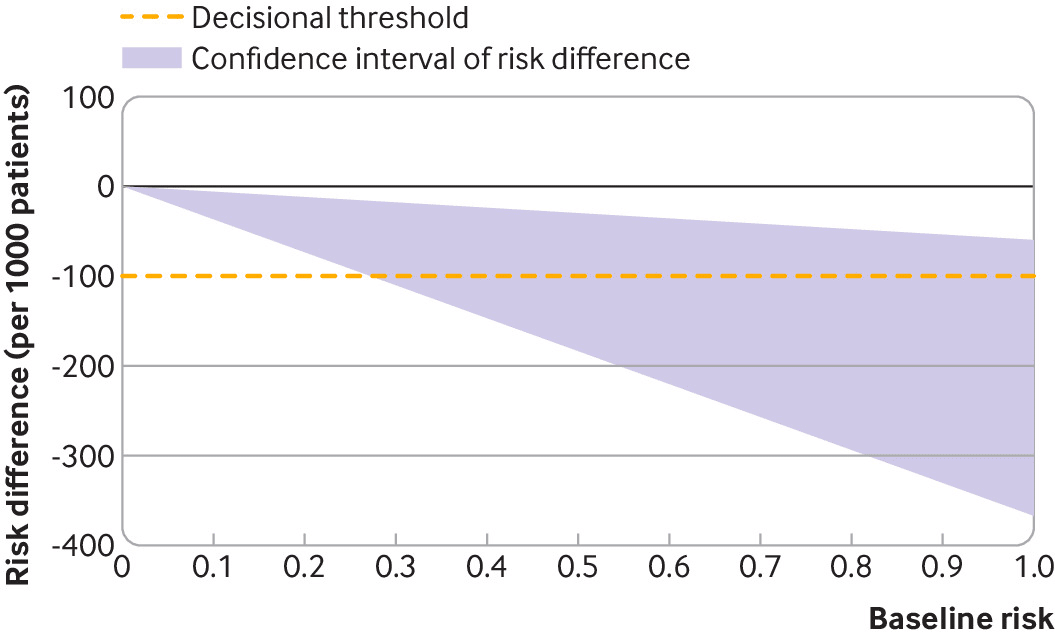
第2の方法は、想定される基本リスクを使用して相対効果を絶対効果に変換する方法です。この第2の方法は、最も一般的に使用され、Cochrane CollaborationとGRADEによって推奨されています。2つの元の方法のいくつかの制限を減らすことができる他の2つのあまり知られていないアプローチを紹介します。
1つは、相対効果と基本リスクの不確実性を考慮したモデリングアプローチです。
もう1つは、個々の研究の基本リスクに条件付けたリスク差を推定する二変量ランダム効果モデルです。メタアナリストやガイドライン開発者がこれらの2つの方法を使用してリスク差を推定できるように、Rソフトウェアを使用したオープンソースコーディングを提供します(コードは付録に記載されており、https://github.com/linlf/RD からデータと共にダウンロードできます)。これらの4つの方法は、頸動脈内膜切除術と頸動脈ステント留置術の比較において、事例研究に適用されています。
要約:
リスク差の信頼区間は、推定値および決定の確実性に関する判断の基礎です。
基本リスクに基づいてリスク差が変化するため、精度の判断は異なる基本リスクを持つ集団に対して個別に行う必要があります。
リスク差と信頼区間を推定するための堅牢な方法が必要です。
メタアナリシスからリスク差を推定する4つの方法が提案されています:個々の研究から得られたリスク差のメタアナリシス、相対効果を絶対効果に変換する方法、相対効果と基本リスクの不確実性を考慮したモデリングアプローチ、個々の研究の基本リスクに条件付けたリスク差を推定する二変量ランダム効果モデル。
これらの方法は、頸動脈内膜切除術と頸動脈ステント留置術の比較において、事例研究に適用されています。
written with Chat-GPT4
方法2:想定される基本リスクを使用して相対効果を絶対効果に変換する方法
BR=ベースラインリスク
RD=リスク差
RR=リスク比
OR = オッズ比
長所:この方法はシンプルで直感的である。
どのようなタイプのメタアナリシスにも使用できる。
コクラン共同計画やGRADE作業部会など、ほとんどの方法論部会で推奨されている。
欠点:この方法は、ベースラインリスクの変動性を考慮していない。
ベースラインリスクの不確実性を想定していない。
結果としてのリスク差の変動は、相対効果の変動のみから導かれる。
全体として方法2は、想定されるベースラインリスクを用いて、プールされた相対効果をリスク差に変換する簡単で直感的な方法である。ほとんどの方法論グループによって推奨されている。しかし、この方法ではベースラインリスクのばらつきが考慮されていないことに注意する必要がある。
written with Chat-GPT4
方法3:ベースラインリスクの不確実性をシンプルなマイクロシミュレーションを用いてモデル化
このアプローチは、同時に2つのエビデンスを考慮する必要がある場合に特に役立ちます。比較効果に関するエビデンスの最もバイアスの少ない推定値は、通常、ランダム化試験のメタアナリシスから導かれますが、実世界のベースラインリスクは、対象とする集団に対してより一般性と適用性が高い別の情報源(例えば、集団ベースの研究やレジストリ)から導かれることが望ましいです。
この方法の適用では、プールされたリスク比またはオッズ比、およびその信頼区間と、ベースラインリスクとその信頼区間が必要です。一般的な統計ソフトウェアが必要であり、通常、メタアナリシスソフトウェアでは実装されていません。付録では、このシンプルなマイクロシミュレーションのRコードを提供しています。
この方法は、個々の患者の試験をシミュレーションし、個々の結果を集計してグループの平均と分布を生成することでリスク差を推定する(モンテカルロシミュレーションに似ている)。したがって、この方法の主な特徴は、「個人のサンプリングから目的の患者群を構築する」ことであり、一度に一人の個人をシミュレーションし、集約された個人のシミュレーション結果すべてからコホート全体の平均結果を算出する22。モデルを実行するたびに、利用可能なベースラインリスクの平均値と標準偏差で定義される分布からランダムに引き出されたベースラインリスクの患者を選択する。この情報は通常、対象となる患者群に最も近い特徴を持つ研究または一連の研究から得られたものである。この患者はまた、利用可能なリスク比(又はオッズ比)の平均と標準偏差によって定義されるリスク比(又はオッズ比)の分布から無作為に引き出されたシミュレーションリスク比(又はオッズ比)を持つことになる
Translated with DeepL
written with Chat-GPT4
方法4:二変量ランダム効果モデル
二変量ランダム効果モデルに基づく一段階のメタ分析モデル
治療群と対照群のリスクを共同で分析し、ベースラインリスクに基づいて条件付き効果を計算
この方法で使用されるモデルには、二変量一般化混合効果モデルや二変量ベータ二項モデルが含まれる
方法の適用
分析に必要なデータは、方法1で必要なデータと同様
このアプローチは現在メタアナリシスソフトウェアでは利用できず、一般的なソフトウェアパッケージと統計コーディングの知識が必要
利点と欠点
二変量アプローチを使用することで、平均ベースラインリスクでリスク差の信頼区間が狭くなる
方法2で指摘された問題を解決し、ベースラインリスクが増加するにつれてリスク差の信頼区間が広がることがない
方法2とは異なり、ベースラインリスクにわたる相対効果の可搬性を仮定する必要がなく、方法1とは異なり、個々の研究から推定されるリスク差に正規分布を強制する必要がない
事例研究への適用
内頸動脈内膜剥離術とステント留置術の効果を比較した8件の試験のデータに二変量一般化混合効果モデルを適用
図4では、平均ベースラインリスク8%で信頼区間が最も狭く、ベースラインリスクが増加または減少するにつれて広がることが示されている
このモデルは特定のベースラインリスクに対するリスク差と95%信頼区間を提供する

