
サンプリングレートは表現したい周波数の倍で足りるのか?
少し前に量子化 bit 深度の note を書いたので、次はサンプリング (標本化) の話かな?というところなのですが、こちらは量子化よりも根が深く物議を醸しそうな危険があります……。
また、「サンプリング定理 (標本化定理)」など理論的な面が目立つ分野になっていて、しっかり紐解こうとすると一気に難解な記述になってしまうため、そこにも注意する必要があります……。
そんな闇の深いテーマの入口を気楽めに覗けないかといろいろ検討した結果、「サンプリングレートは表現したい周波数の倍で足りると言われるけど実際問題どうなの?」という端的なところに絞ったものを書いてみることにしました!
量子化に引き続き実用への直結は難しい話ですが、デジタルオーディオへの向き合い方を再考するきっかけになれば嬉しいです!
サンプリング定理
今回のテーマの「サンプリングレートは表現したい周波数の倍で足りる」の部分は、「サンプリング定理 (標本化定理) 」を元にした主張になっています。サンプリング定理は要約すると下記のようなものです。
サンプリング定理 :
ある信号が fs/2 (Hz) より小さい周波数に帯域制限されているとき、サンプルレート fs (Hz) でサンプリングするとそこから元の信号を完全に再構成することができる。また、この場合の fs/2 は「ナイキスト周波数」と呼ばれる。
本稿では証明などの定理自体に深く触れる内容は、話がややこしくなるので一旦避けることにします。
この定理が現実的なデジタルオーディオでもそのまま適用されると受け入れるなら「サンプリングレートは表現したい周波数の倍で足りる」という結論になり、本稿は終わってしまうように感じると思います。
しかし、実際に確かめてみるとどうなっているのでしょうか?
実際に確かめてみる
いろいろな「ナイキスト周波数より低い周波数のみを含む音源」について、どう表現されるのか確かめていきます。
サンプリングレートは 48kHz とします。Wav ファイルとしては 48kHz 16bit LPCM を使いますが、量子化 bit 深度に関してはあまり気にしません。(影響があることはあるのですが……)
今回見ていく音源の Wav ファイルを先に下記にまとめて用意しておきます。非常に高い周波数の音も含まれるので再生音量などはご注意ください……。
周波数確認 Wav ファイル集
それではいくつか例をみていきましょう!
23999.9Hz の Sin 波
まずはギリギリの例です。しかし、当然 23999.9 < 24000 = fs/2 なので、ギリギリとはいえサンプリング定理上は完全に再構成されるはずの音源です。
ここまでの周波数になってくると多くの人類の可聴域の外なので、耳で聴くのは諦めて「波形の形状を目で確認」「ピークメーターや RMS メーターで確認」などをやってみます。
まず、波形は下図のようになります。波形の振幅が 0 に近くなったり戻ったり 5 秒間かけて変化しています。所謂「うなり」のような状態です。

ピークメーターや RMS メーターも、その変化に合わせて大きく値が変化します。
これは音量が一定の Sin 波だったはずの波形なわけですが、果たして「元の信号に完全に再構成されている」と言えそうでしょうか?
11999.9Hz の Sin 波
23999.9Hz は聴こえないので実感が無かったかもしれませんが、今度は 11999.9Hz と常人でも聴こえる周波数になります。また、11999.9 < 12000 = fs/4 なので、ナイキスト周波数の更に 1/2 の周波数までしか含まれていません。サンプリング定理上の完全な再構成も余裕?のはずです。
さてまずは聴いてみましょう。「11999.9Hz の綺麗な Sin 波」が聴こえるでしょうか……?
聴くファイル : [Tone01_Sin11999_9.wav]
比較ファイル : [Tone01_Sin12000.wav]、[Tone01_Sin11999_5.wav]
よく聴くとゆっくり音量が揺れるのが分かりますでしょうか……?比較しやすさのために揺れの無い 12000Hz 版と揺れの速い 11999.5Hz 版も用意していますので聴き比べてみてください。揺れが多少速いほうが若干認識しやすい気がします。
波形の形状も確認してみると、こちらも振幅が揺れているのが観測できます。周期は先程の半分の 2.5 秒になっています。

メーターを見てみると、ピークメーターは振幅に合わせて揺れるものの、RMS メーターはあまり揺れません。この理由は波形を拡大してピークが大きいところと小さいところを比べてみると形状の違いでなんとなく想像がつくかもしれません。(本題では無いので詳細は端折ります……)


さて、RMS メーターの揺れは小さいものの、音としては認識できる揺らぎが存在することが分かりました。こちらに関しても「元の信号に完全に再構成されている」と言えそうでしょうか?
7999.9Hz の Sin 波
さてさて……、徐々にどういう話か分かってきたでしょうか?どんどん周波数は低くなります!7999.9 < 8000 = fs/6 まで来ました。もう殆どの人が聴こえると思います。また、ナイキスト周波数に対しても十分にマージンが取れているといえます。
こちらも比較のために 8000Hz、7999.9Hz、7999.5Hz を用意しました。聴いてみましょう。
聴くファイル : [Tone02_Sin7999_9.wav]
比較ファイル : [Tone02_Sin8000.wav]、[Tone02_Sin7999_5.wav]
やはり、音量が揺れているように聴こえるのではないかと思います。これも揺れが速いほうが認識しやすいでしょうか……?
波形としては下記でピークの揺れは少し減ってきていますが、まだ見てすぐ分かるくらい揺れています。

さて、「元の信号に完全に再構成されている」と言えそうでしょうか?
5999.9Hz、3999.9Hz、2999.9Hz、1999.9Hz、999.9Hz の Sin 波
こうなってくると、どこまで低い周波数まで影響があるのか確認したくなってきます。面倒になってしまったので一気に聴いてみましょう、笑。それぞれ綺麗な Sin 波が聴こえるでしょうか……?
聴くファイル : [Tone03_Sin5999_9.wav] ~ [Tone07_Sin999_9.wav]
比較ファイル : [Tone03_Sin6000.wav] ~ [Tone07_Sin1000.wav]、[Tone03_Sin5999_5.wav] ~ [Tone07_Sin999_5.wav]
個人差もあるかもしれませんが、999.9Hz でも十分揺れの認識ができそうです。おぉ……?
また、999.9Hz では波形の視覚的なピークの揺れは大分収まっています。それでも聴感上の違いを感じられることに人間の聴力の凄さ?を感じますね。

というわけで、なんとナイキスト周波数の 1/24 でさえ「元の信号に完全に再構成されている」とは言いづらい状況です。一気に行ったハズなのに底が見えません……。
479.9Hz、239.9Hz、119.9Hz、59.9Hz の Sin 波
こんな低周波数の音まで比較することになるとは想像できたでしょうか……?そろそろ区別が付かなくなってくるでしょうか……?
聴くファイル : [Tone08_Sin479_9.wav] ~ [Tone11_Sin59_9.wav]
比較ファイル : [Tone08_Sin480.wav] ~ [Tone11_Sin60.wav]
だんだん揺れは分かりにくくなっているものの、59.9Hz での揺れでさえ割と認識できそうです……。
59.9Hz というと 59.9 < 60 = fs/800 でナイキスト周波数のなんと 1/400 です。「元の信号に完全に再構成される」とは一体何だったのでしょうか……?
なぜ完全には再構成されないのか?
確認してみた結果としては、「ナイキスト周波数から大幅にマージンを取ってさえ元の信号に完全には再構成されない場合がある」となるのですが、これはサンプリング定理と矛盾するのでしょうか?
完全には再構成されない理由についてしっかり掘り下げると一気に難解になってしまうのですが、何も補足無しでは流石に納得するのが難しいところになると思うので、ここもなんとか端的に説明してみましょう……!
まず、サンプリング定理上の「再構成」はどのようなものなのかを確認します。
サンプリング定理上の「再構成」手順 :
各サンプルを「サンプリング関数 (sinc 関数)」に各サンプル値を掛けたもので置き換える。
サンプリング関数は下記のような形で、2 sample を周期とした sin(x)/x の形の関数です。
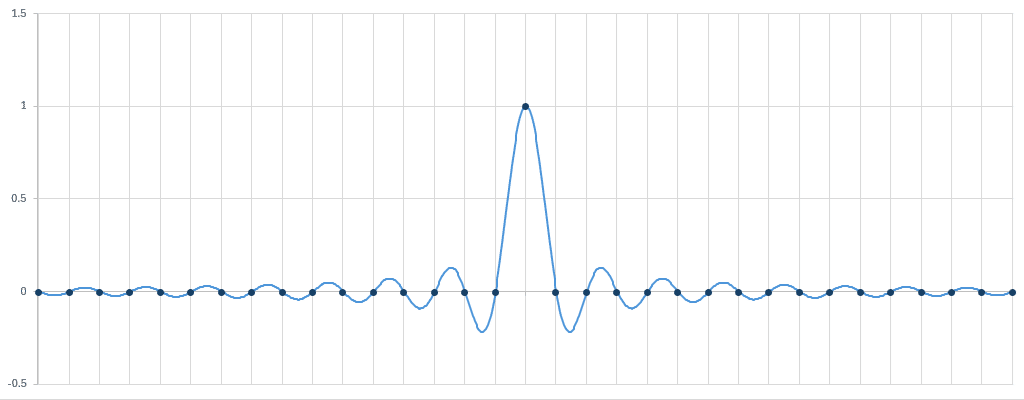
また、サンプリング関数は下記の特徴を持ちます。
時間軸の前後に無限
収束が遅い (1/x 的な収束)
まず、時間軸の前後に無限であることから、この関数をそのまま実際の DA 処理に採用するのは不可能です。そのため近似的な処理をすることになるのですが、そうなると重要なのは近似の精度になります。
サンプリング関数を途中で打ち切る場合、どの程度の精度が期待できるものなのでしょうか?
精度を保ちづらい簡単な例として、サンプリングレート 48000Hz 上での 23999.9Hz のようにナイキスト周波数より少しだけ小さい周波数の Sin 波が挙げられます。まずは、サンプリングレート 32Hz 上での 15Hz の Sin 波という例で見てみましょう。

サンプリングの様子を見ると、元の Sin 波の山谷付近にサンプル点が来る場合 (図中の A) と、山谷付近にはサンプル点が無い場合 (図中の B) があることが分かると思います。
ここで、「元の山(谷)はどのサンプル点からの影響によって再構成されるのか?」を考えます。
図中の A 地点のようにサンプル点と山が重なっている場合、元の山の高さは山の位置のサンプル点によってのみ再構成されるといえます。つまり、サンプリング関数の打ち切りの影響を受けません。
一方で、図中の B 地点のようにサンプル点の間に山がある場合、山の再構成には非常に広い範囲のサンプル点が使用されるといえます。直感的にも B 付近には山に近いサンプル点が存在しないことから、付近のサンプル点だけでは殆ど再構成できないことが分かると思います。
こういったケースではサンプリング関数の打ち切りの影響がとても大きく、この例では B から A 地点に届かない 0.25s 未満程度の長さで打ち切ってしまうと、大きく精度を落とすことになります。
サンプリングレート 48000Hz 上での 23999.9Hz の Sin 波の例で考えると、この長さは 2.5s です。(もっと極端に 23999.99999Hz とかを考えると、25000s ≒ 7hour とかになります……)
2.5s のサンプリング関数を DA に使用しようとすると再生遅延が 1.25s 発生するなど恐らく使い物にならないので、実用上を考えると再生周波数によっては精度が落ちてしまうのが避けられないということになります。
また、A のような山谷と B のような山谷が交互に現れると精度の低下が音量の揺れのような形で現れ、認識しやすくなります。そうなる条件は、「ナイキスト周波数と簡単な整数比の関係にある周波数から少しだけずらした周波数」となっていて、これを元に Sin 波の周波数を選定して「実際に確かめてみた」ということでした。
サンプリングレートは表現したい周波数の倍で足りるのか?
ということで、実際に確かめてみるとナイキスト周波数から大幅にマージンを取っても元の波形の周波数によっては音の乱れが生じることが分かりました。
この結果からの結論としては、現実的なデジタルオーディオ上では「サンプリングレートは表現したい周波数の倍で足りる」とは言えないことになります。
適正なサンプリングレートを考える (中締め)
一方で、適正なサンプリングレートを考える意味では、「足りる」と言えそうな位までとにかくハイレートにするほうが良いとは思っていません。
サンプリングレートを上げていくと (厳しい条件下での) 表現が保たれるメリットの割にデータ容量や処理負荷などのデメリットが目立ってきてしまいます。実際に使用するサンプリングレートを考える場合は状況に合わせてバランスを取る必要があります。
結局のところ物事はシンプルではなく「何を捨てて何を得るか?」という話にしかならないので、大切なのは表現と真摯に向き合うことですね!
(何この締め……)
「理想的な LPF」が時間軸に与える影響
中締めしましたが、もうちょっとだけ続きます……。ここからは余計に納得が難しい内容になってくると思うのですが、一応触れておかないとタイミングを逃しそうなので書くだけ書きます……。
今回は「倍で足りない」原因として現実の DA 処理がサンプリング定理に沿った時間軸の前後に無限な処理ではないことを挙げたのですが、それなら仮にサンプリング定理に沿った処理をデジタルオーディオに持ち込むことができればきちんと「倍で足りる」のか?という疑問が湧きます。
サンプリング定理に沿った DA 処理は各サンプルのサンプリング関数への置き換えと説明しましたが、これは「理想的な LPF」の適用を意味します。
また、サンプリング定理に沿った AD 処理を考える際にも「理想的な LPF」が必要です。現実の様々な波形は帯域制限されてはいないので、帯域制限をするために使用します。
「理想的な LPF」は前後に大きな時間軸への影響が存在します。フィルターの時間領域への影響が音にどう響くのかは以前 EQ について書いた時に少し触れています。
つまり、「理想的な LPF」が理想的なのはあくまで周波数領域にとっての話であり、時間領域にとっては前後の無限の時間に影響を与えてしまう理想的とは言えない処理になっています。
仮にサンプリング定理に沿って「理想的な LPF」を組み込んだ AD/DA 処理が可能だとして、その処理は時間領域も含めた元の「音」を再現する処理にはならないということです。
「リサンプリング」と「エイリアシング」
関連して結構重要な話として「リサンプリング」と「エイリアシング」が残っています。
認識できる音の乱れが生じやすい条件を、リサンプリングも含めて拡張すると下記のようになります。
正確に等間隔なサンプリング (大体のデジタルオーディオではそう)
正確に規則正しい波形
波形の周期と(リ)サンプリングの間隔が丁度良い比率から僅かにズレている
こういった条件に該当する例は少ないように思われるかもしれませんが、オーディオ処理を行う際に非常に該当しやすいパターンが存在します。
「わずかな再生速度(ピッチ)の変更」です。
わずかな再生速度変更での音質劣化は、実感した経験がある人もそれなりにいると思います。個人的にはこのあたりの現象は「時間領域エイリアシング」として捉えています。
「エイリアシング」はナイキスト周波数以上の高周波数領域が低周波領域へと折り返す現象として知られていますが、時にもう少し広い意味で取られていると思います。以前に少し触れました。
この「時間領域エイリアシング」は最初に挙げた 3 つの条件下で目立ってくるので、対策としてわざと条件を微妙に崩すような処理が有効になることが考えられます。サンプリング軸のディザリングとも例えられるかもしれません。
おわりに
読み返してみてもなかなか納得の難しい内容だなぁと思うのですが、、、実例として音の乱れの発生を示せたということを起点に、いろいろと理解が広がっていくと良いなと願うばかりです。
また、毎度のことですがこんなノリでも間違ったことは書かないように凄く気をつけているので、お気付きの点があればお気軽に (あとどうかご丁寧に……) お知らせくだされば嬉しいです!
あと、しばらく Sin 波聴きたくないです……笑
参考
標本化定理 - Wikipedia
