見出し画像

EQ を IR で知る

Prismaton

EQ(equalizer) は音の質感を調整する上でほぼ必須のものになっていますが、それでいてとても奥が深く、しっかり理解するのは難しいものだと思います。

EQ の作用の捉え方としては、「周波数(振幅)特性を調整するのが主作用で、副作用として位相ずれや群遅延が起こる」のように考えている人が多いかと思います。もちろんこれは間違いと言うわけではないです。

ですが、EQ の作用には重要な別の捉え方があります。それは、「EQ は IR(Impulse Response) の適用であり、その結果として周波数(振幅)特性の調整が出来る」というもので、これを知る事をテーマとして本稿を書きました。

この捉え方の何がポイントかというと、アタック感など「周波数特性では表現されない音の変化」に対しての認識解像度が上がります！重要な人には重要ですね！笑

噛み砕き気味に書いているので、細かい正確さとしては多少不足がありますが……、全体感としての誤解がなく実用的な知識として使ってもらえるように頑張ってみましたのでよろしくお願いします〜〜

ディレイの集合体と IR

EQ は短いディレイの集合体です。例えば、簡単なローパスフィルターの一種として移動平均フィルターが挙げられます。

移動平均ローパスフィルターのディレイ構成

この例では 0 ～ 3 sample のディレイを 0.25 倍ずつ組み合わせています。高い周波数の波形が小さくなり、低い周波数の波形は概ね残るローパスフィルターになっています。

移動平均フィルターで高い周波数の波形が小さくなる様子
移動平均フィルターで低い周波数の波形が概ね残る様子

ハイパスフィルターは、例えば元波形からローパスフィルターの値を引くような形にするとできたりします。 (位相の関係で上手くいかない場合もあります)


「元波形 - 移動平均」ハイパスフィルターのディレイ構成

ハイパスフィルターの場合も移動平均フィルターと同様に、「ディレイの集合体」と見なせることが分かると思います。バンドパスフィルターやノッチフィルターなど他のものに関しても、EQ は全て「ディレイの集合体」として表現することができます。

更にこの「ディレイの集合体」というものですが、実のところ「IR の適用」と全く同じ概念で、図に示した各ディレイ構成がそのまま IR になっています。

EQ のように「ディレイの集合体」で表せるオーディオ処理について分類すると下記のようになります。

  • ディレイの集合体で表せるオーディオ処理

    • IR の適用(同じ概念)

    • EQ

    • フィルターと呼ばれるもの (オールパスフィルター、コムフィルターなど)

    • ディレイ / リバーブ (歪みやモジュレーションを含まないもの)

  • ディレイの集合体で表せないオーディオ処理

    • ディストーション / エンハンサー など歪みを含むもの

    • コンプレッサー / ダイナミック EQ など

    • モジュレーションを含むもの全般

    • その他、複雑なエフェクトや自然界に由来する処理など

実は周波数特性の分析などは、この「ディレイの集合体で表せる」ことを前提にしています。

(定義的には「線形時不変 (Linear Time-Invariant)」と呼んだりしますが、専門的な話になっちゃうので省略です。)

(例えばアンプの歪みを再現するのに周波数特性分析するのって本来的にはちょっと変なんですね……。)

ここまでをまとめると、 「ディレイの集合体」と「IR の適用 」は同じ概念で、EQ はその中に含まれるということになります。

FIR / IIR

FIR / IIR はそれぞれ Finite Impulse Response / Infinite Impulse Response の略で、IR が有限か無限かによって呼び分けられます。

EQ などフィルター系の信号処理の話をする際には良く出てくる用語だと思いますが、既に EQ の話なのに自然に IR の話になっていて、本当に繋がりが深い概念だということが分かると思います。

先程の例の移動平均フィルターは FIR ですので IIR の例を紹介します。下記は 1 sample 毎に 0.5 倍になっていくようなフィードバックディレイで、IIR のローパスフィルターになっています。(この考え方はオーディオ以外にも時間変化する値の急変動を抑える場合などに重宝します)

IIR のローパスフィルターの IR

フィルターの設計・実装面での FIR と IIR の違いは、処理負荷などに影響するため重要なものなのです。ですが、処理の都合を無視して音質評価のみに絞った話であれば、FIR は IIR でも表現できますし、IIR を FIR で近似することも十分な長さの IR として表現すれば可能なので、これがどちらかというのは実は気にしすぎなくて良いです！笑

IR の分析

というわけで話は本筋に戻ります。EQ の分析のためにはその IR の分析が有用ということが、なんとなく想像が付いてきたかなというところで、具体的な IR の分析方法について一気に触れていきます！

分析したい EQ の IR

例えば、上記のような IR を持つ EQ があるとします。ここで注目するのは下記の点です！

  • (1) IR 時間

  • (2) 最大ピーク位置

  • (3) ピーク回数

IR の分析

まず、IR 時間についてです。これは IR の影響で元波形がどの程度時間軸方向に広がってしまうか？を表します。これが長い場合、周波数特性が調整されるのとは別に、少しずつリバーブがかかったような音に変化していきます。

IR 時間は EQ のカットオフ周波数が低いほど長く (波長に比例するような形)、またきついカーブのものほど長くなります。

IR 時間はある程度目視などで確認もできますが、スレッショルド以上になっている時間を数値化してもいいかも知れません。(RT60 のように IRT60 などとして -60dB をスレッショルドとするなど)

次に最大ピーク位置です。これが後ろのほうに位置している場合、プリリンギングと呼ばれる現象が発生します。極端なケースでは元波形のアタック位置より手前に音が鳴り出すのがはっきり分かってしまい、不自然なアタックになってしまいます。

最大ピーク位置は後に解説する Linear Phase / Minimum Phase の違いによって大きく変わります、

最後にピーク回数についてです。ピーク回数が多いほど元波形のアタックが分散して、崩れやざらつきを感じる音になっていきます。(細かく言えば回数だけでなくピークの数値や鋭さなども影響します)

ピーク回数は、カーブのきつい EQ や複数のカットオフを持つ EQ で増えることがあります。

この 3 つの要素、特に後の 2 つは基本的にはアタック感への悪影響に相当します。更にこれらの効果は別の EQ で相殺することはできず、EQ をかけるたびに積もっていくことになります。

Linear Phase

Linear Phase は EQ の特性を語る上で頻出する言葉だと思います。言葉の意味からすると位相特性が線形ということなのですが、そうはいってもよく分からない感がありますよね？

しかし Linear Phase EQ を IR の特徴で見ると非常にわかりやすく、その IR は時間軸で前後対称になっています。Linear Phase EQ の強みはこの対称軸でタイムアライメントを取ることによって位相特性が揃うことで、複数 EQ を並列使用する際の周波数特性コントロールが容易であったり、チャンネル毎に別の EQ を使用する場合に位相特性を揃えることができたりする点です！

Linear Phase EQ の IR 例

(IR 全体の時間をずらすのが位相の線形変化に相当し、位相特性が線形ということは IR 全体の時間をずらせば位相特性が揃うということになります)

逆に Linear Phase EQ には (特に今回注目している話題にとっては) 大きな弱点があります。前後対称の形状のため、最大ピーク位置がかなり後ろのほうに来てしまっている点です。IR 時間の半分程の位置に来ることになるため、IR 時間の影響を受けて最大ピーク位置が後ろに来ることになります。

カットオフ周波数が低かったりカーブがきつかったりする Linear Phase EQ はプリリンギングが大きいというのは聞いたことがある人もいると思いますが、完全に事実です！笑

Minimum Phase

Minimum Phase は Linear Phase の問題点が一部で指摘されるようになってきて、一部で注目され始めた言葉です。

定義は若干ややこしいですが、平たく言うと最大ピーク位置が 0 sample 目にきて、徐々に弱くなっていくような IR を指します。つまりプリリンギングが発生しないということです。

Minimum Phase EQ の IR 例

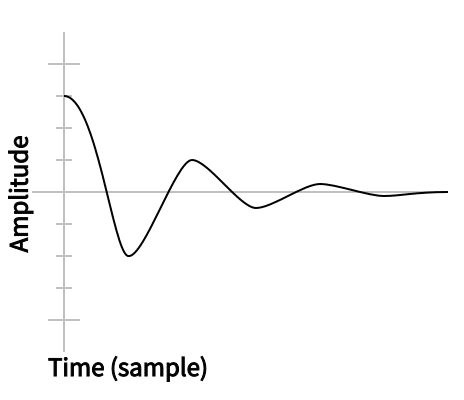
もちろん位相特性は揃わないのですが、位相特性が揃う特性を活かす必要がない場面では、特に問題にはなりません。

アタック感を大事にする EQ の使用法

ここまで駆け足で来ましたが、アタック感を大事にするという視点でまとめると意外とシンプルな話になり、下記のようになります！

  • EQ 使用は必要最低限に！

  • きついカーブの EQ はなるべく避ける

  • なるべく Minimum Phase EQ を選ぶ

  • Linear Phase EQ は本当に必要な場合に絞る

多分、良いエンジニアさんが教えてくれるようなこととほぼ同じ内容だと思うので、是非参考にしてもらえばと思います～

おわりに

EQ の IR の分析についてまとめてみましたが、今回はなかなか有用な情報になったのではないかなぁと思っています。

分量的に前提としてしまった知識があったり、端折った中にも興味深いトピックがあったりはしますので、疑問質問などはお気軽に聞いてもらえたらと思います！


この記事が気に入ったらサポートをしてみませんか？