
【コンピュータの内側】第3回 「論理演算」
前回の予告通り、今回は、論理演算によって四則演算のうちの「加算」が可能であることを示します。
二進法
私達は、数を「0, 1, 2, 3, 4, 5, 6, 7, 8, 9」という10の記号を使って表します。これを十進法と呼び、記号中の最大数である9の次は「繰り上げ」をおこない10とすることで、どこまでも大きな数を表現することができます。
コンピュータのように巨大なシステムを設計する際、無駄な複雑さはできるだけ回避したいところです。10もの記号を用いて数を表現するというのは愚策です。
ということで、なるべく数の表現方法を単純化し、2つの記号「0, 1」のみで完結するようにしてみましょう。十進法と基本的には同じですが、記号中の最大数が1となるため、1の次は繰り上がって10となります。

2つの値のみで表現が可能ということは、モノの有無、扉の開閉、スイッチのオンオフ、電圧の高低など、明らかに単純な機構で実装できそうです。これは二進法の大きなメリットでしょう。
コラム「二進指数え法」
もう一つ、我々が利用している身近な数の表現として一進法が挙げられます。私達は指で数を数える際に、折った指の数(または立てた指の数)で数値を示します。これは一進法と言えます。
しかし、指は「立てる」「折る」という2値の表現ができるので、二進法で数えることもできます。指が10本あれば、2の10乗、つまり1024もの数値を表すことが可能です。
二進法の足し算
今回の目的は四則演算ですので、まずは単純な加算(足し算)について考えます。
a: 1 + 0 = 1
b: 11+ 5 = 16
これは二進法では次のように表現します。
A: 1 + 0 = 10
B: 1011 + 101 = 10000
見ての通り、二進法は十進法と比べて桁数が大きくなります。コンピュータを作るには、もっと単純化したいところです。
ところで、私達は桁数の多い計算を単純化する方法を知っています。そう、「筆算」です。筆算は、桁数の多い計算を一桁ずつに分解して行うため、コンピュータが求める「単純化」と相性が良いのです。早速やってみましょう。

今更言うこともありませんが、筆算では右の桁から順に計算していきます。この場合、一番右の桁はともに1ですので1+1=10となり、この桁の解は0、繰り上げが1です。
次桁は1と0ですが、前桁の繰り上げ分があるため1+0+1=10となり、同じくこの桁の解は0、繰り上げが1です。
半加算器
さて、これで私たちが作りたい「加算器(足し算を行う機械)」の全貌が見えてきました。筆算のように1桁のみを計算する機械を作成し、無数に繋ぎ合わせれば良いのです。繋ぎ合わせる機械の数は、計算できる桁数の上限を表します。

さて、単純化できたとはいえ、いきなり完全な加算器を作るのは大変なので、まずは最も簡単なバージョンである「一桁しか計算できない加算器」について考えます。このバージョンでは一桁のみにフォーカスするため、繰り上げという概念を無視できます。
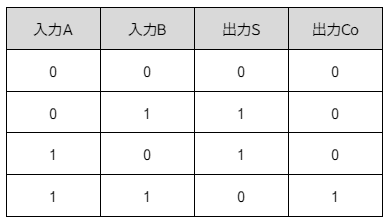
計算対象となるデータ(以後オペランドと表記する)が2つの場合、二進法一桁の加算では以下4つのバリエーションがあります。

この表をみると、出力が1となるのは中間の2パターンであることがわかります。ここで数理論理学を思い出しましょう。真を1、偽を0とすると、これは次のように言い換えることができます。
(Aでなく かつ Bである)または(Aであり かつ Bでない)ならば 真
もうおわかりでしょうか。これを論理式になおしてみます。
出力S: (¬A ∧ B) ∨ (A ∧ ¬B)
この論理式こそが「一桁しか計算できない加算器」です!言い換えれば、論理演算によって1桁の加算を行うことができました。
次に、繰り上がり桁の出力について考えましょう。4つのバリエーションの内、繰り上がりが発生するのは2つのオペランドが共に1となった時のみです。
出力Co: A ∧ B
これで、繰り上がりを出力するロジックが完成しました。2桁以上の加算を行うには、前の桁の繰り上がり出力を入力として加える必要がありますが、実は最小桁の加算は現状のままで利用できます。前の桁が存在しないためです。これを「半加算器(Half adder)」と呼びます。

全加算器
前述の通り、半加算器に出来るのは最小桁の加算のみです。ここからは、2桁以上の計算を行えるよう、入力Ci(前桁のCoの入力ポート)を追加していきます。
といっても、やることは半加算器と同様です。まずは真理値表を作成しましょう。入力が3つあるため、バリエーションは8通り(2の3乗)になります。

次に、出力Sの論理式を組み立てます。出力Sが真となるのは、3つの入力のうち1の数が奇数個である4通りです。
・¬A ∧ ¬B ∧ Ci
・¬A ∧ B ∧ ¬Ci
・A ∧ ¬B ∧ ¬Ci
・A ∧ B ∧ Ci
抽出した4つを or(∨) で繋げば完成です。
(¬A ∧ ¬B ∧ Ci) ∨ (¬A ∧ B ∧ ¬Ci) ∨ (A ∧ ¬B ∧ ¬Ci) ∨ (A ∧ B ∧ Ci)
= ¬Ci (¬A ∧ B ∨ A ∧ ¬B) ∨ Ci (¬A ∧ ¬B ∨ A ∧ B)
出力Coの論理式についても同様です。
(¬A ∧ B ∧ Ci) ∨ (A ∧ ¬B ∧ Ci) ∨ (A ∧ B ∧ ¬Ci) ∨ (A ∧ B ∧ Ci)
= A ∧ B (¬Ci ∨ Ci) ∨ Ci (¬A ∧ B ∨ A ∧ ¬B)

あとは簡単。n桁の加算器を作るには、半加算器1つと全加算器n-1個を組み合わせるだけです。

まとめ
今回の目的は、「論理演算によって四則演算が可能である」を示すことでした。四則演算のうち、加算については達成できたかと思います。
減算、乗算、除算については後回しにして、次回は、今回導いた論理式をもとに論理回路を作成します。論理回路はコンピュータ上で視覚的にシミュレーションすることが出来るので、実際の動作を理解するのに役立ちます。
