
方眼紙の上で線分を分割
方眼紙の上で図形を描いている時に、ある斜めの線分をn等分したいときはどうしたらいいでしょうか。
目盛をかぞえて、ちょうど中央をさがす、というのももちろんありです。でも、末端が方眼にちょうどのっかっていないと、かなり面倒ですよね。方眼紙の上では垂直や水平な線を描くのが簡単なので、それをつかって手早く等分する方法を紹介します。(老眼には1 mm方眼を数えるのがつらい、というのもあるのですが…)
方眼紙のうえにてきとうに引かれた、紫の直線を2等分する場合には、
(1) まず、その右側に、方眼を使って3本の平行線を等間隔に引きます。

(2) 次に、紫の線の上下端から、水平線を引いて、平行線と交わらせます。

(3) 上下の交点をななめにつなぐ直線を引き、

(4) まんなかの交点から水平線を引き、もとの線分に戻すと、そこが二等分点です。

(5) 同じ要領で、3分割も簡単にできます。こんどは平行線を一本増やし、斜めの線を引いて、

(6) また水平線を引くと、もとの線分は3等分になります。
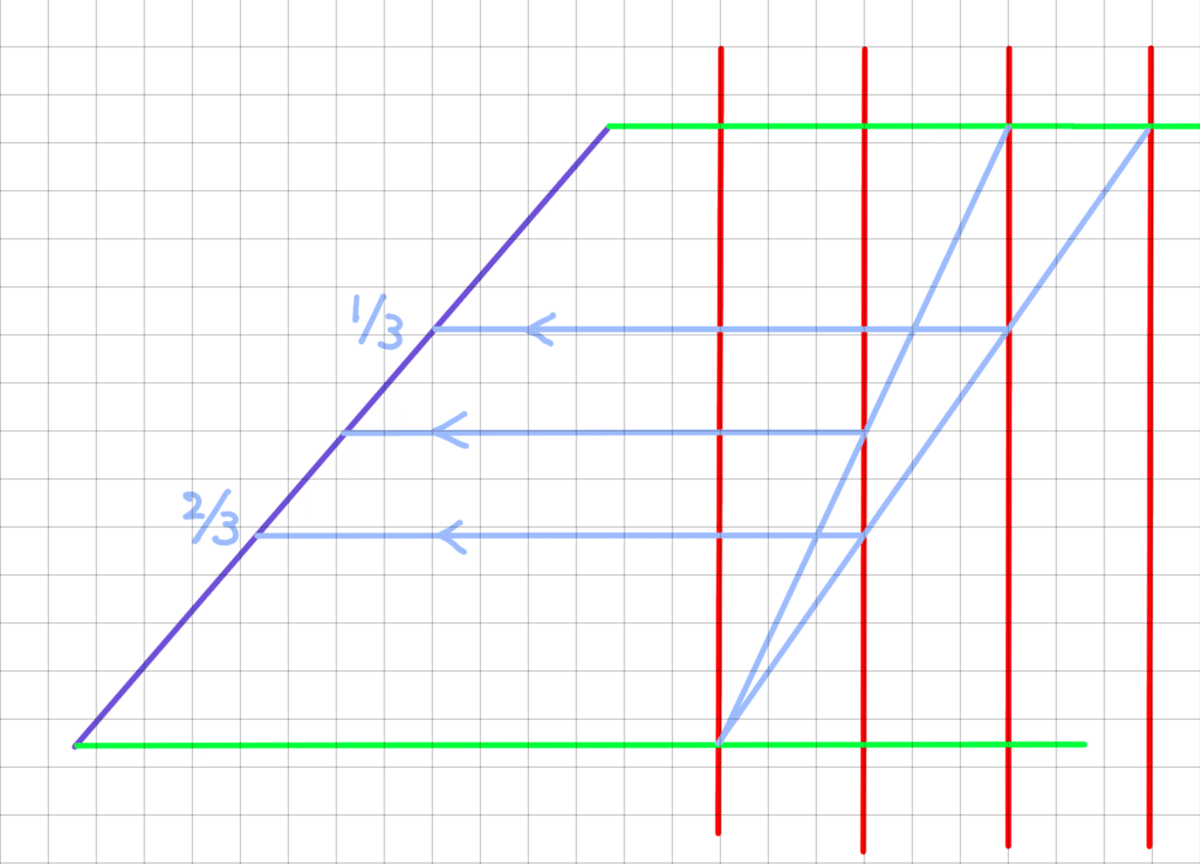
うまい補助線をひくことで、等間隔に引かれた平行線の比率を、任意の線分に「写しとる」ことができました。
この発想を応用すると、任意の線分を黄金比分割するのも簡単です。あらかじめ黄金比間隔で平行線を引いておいて、それを線分に写しとればいいのです。
ただし、黄金比は1:1.618...という中途半端な比率なので、そんな中途半端な間隔の平行線を引くのも面倒です。
ここでは思いきって、黄金比を整数比で近似してしまいます。例えば、円周率3.14159...は、22/7あるいは355/133でかなりよく近似できることが知られています。

同じように、黄金比は、いろんな分数で近似できます。(ただし、黄金比はあらゆる数字のなかで、一番分数で表しにくい数なので、あまり正確ではありません)

見ての通り、黄金比はフィボナッチ数列の隣りあう項の比で近似できます(フィボナッチ数列は、0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...という風に、0と1からはじめて、隣りあう項を足すと次の項になるような数列です)。
もともと、手描きの精度で図を描こうという試みなので、あまり厳密に正確に描く必要はありません。ここでは、φ=13/8=1.625で近似することにします。(0.4%だけ大きくなりますが、これは25 cmに対し1 mmほどずれる、と考えると、手作業の精度としては十分すぎるぐらいです。)
(1) 分割したい線の横に、5:8の間隔で平行線を引きます。

(2) 線分の上下端から、水平線をひいて、平行線と交わらせます。

(3) 上下の交点を結ぶ斜線を引き、
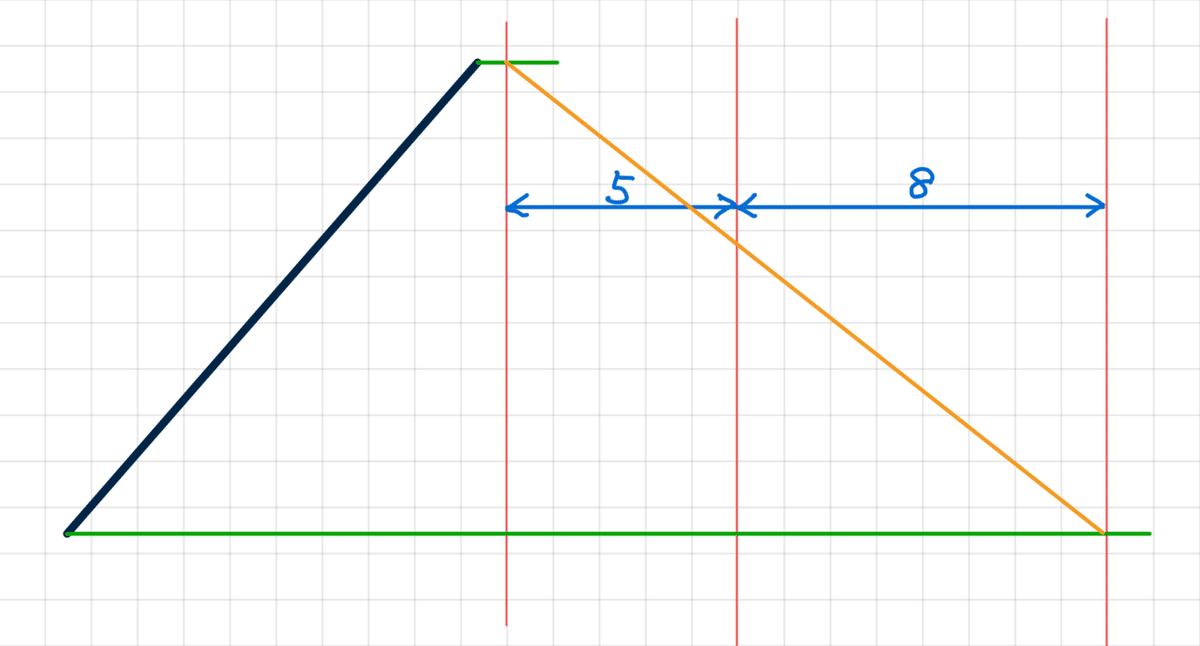
(4) 中央の線との交点から、水平線で元の線分に戻すと、おおよそ黄金比で分割できました!

(5) やや精度は落ちますが、次の図のように見ることもできます。

このようにして、方眼紙の右端と下端に、平行線をいくつか引いておくと、それを手掛りにして線分を自在に分割できます。
