2018 京都教育大学 教育学部 数学領域専攻 学校推薦型選抜 小論文 模範解答
Ⅰ.
下の表は0から15までの10進数を、2進数で示したものである。
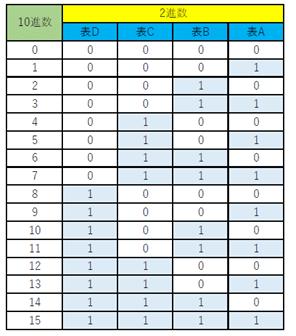
(1)問題のカードDに書かれている数字は、2進数の4桁目が[1]である数字の集まりである。4桁目には、23=8の重みがある。
(2)問題のカードCに書かれている数字は、2進数の3桁目が[1]である数字の集まりである。4桁目には、22=4の重みがある。
(3)問題のカードBに書かれている数字は、2進数の2桁目が[1]である数字の集まりである。4桁目には、21=2の重みがある。
(4)問題のカードAに書かれている数字は、2進数の1桁目が[1]である数字の集まりである。4桁目には、20=1の重みがある。
(5)さらに問題カード内右下の数は、2進数から10進数への変換の際に用いる各桁の「重み」が配置されている。したがって、カードAからカードDまでに該当する数字があるか、ないかを問いかけることにより、2進数の各桁が[1]であるか、[0]であるかを知ることができる。その4桁の2進数について、右下の「重み」の和を得る(=ようするに、2進数を10進数に変換する)ことで数を言い当てることができる。
カードが5枚ある場合には、1~31(24=16を1から15に加える。つまり、2進数で5桁目が[1]になる数を加える)までの範囲の10進数を用い、カードにはそれぞれ2進数の桁の重み(24=16、23=8、22=4、21=2、20=1)ごとに分けた10進数の数を記載し、さらに各カードの右下には(1、2、4、8、16)という2進数の桁数の「重み」を示す数を配置されたカードを用意すればよい。
参考)0から31までの10進数を、2進数で示した表。

Ⅱ.
問1.A=人間である, B=動物である
A⇒B:「人間ならば動物である」
B⇒A:「動物ならば人間である」
問2.
選択 ⑨一つの例で「すべて」と思ってしまう
きれいに切られた三角形の折り紙の各頂点を重ならないように一つの点に集めると、その点を通る直線ができる。それゆえ、三角形の内角の和は180度だと証明できる。さらに、この証明はどの三角形にも当てはまることから、一つの例で「すべての三角形が180度だ」ということが一般化される。したがって、一つの例で「すべて」が説明されうる事象もたしかにある。しかし、正三角形は線対称な図形であるけれども、この一事例をもって、すべての三角形が線対称な図形だとは言えない。このように算数・数学を学ぶ上では、一つの具体例から一般化が可能な事柄と不可能な事柄がある。ある例で上手くいったことが、他の例でも上手くいくかを個別に検討するには、いわば無数の実験が必要となる。それゆえ、理論的に一般化が可能かどうかを見定めるために、証明という手続きがある。以上より、一つの例で「すべて」と思ってしまうことはダメなのである。(393字)
