
【過去問】共テR03 物理 第3A(光学)
その場で「ダイヤモンドが明るく輝く理由」を考えさせる良問です。
当然誘導問題になっています。ちゃんと誘導サーフィンにのりましょう。
特に、どの受験生も初めて見るであろう問3の入射角-臨界角のグラフを冷静に読み解けるかどうかが全問正解への鍵となっています。
問1
光学の常識を問う問題です。
まず、異なる媒質に光が進むとき何が変化するか、しないか。
結論:振動数$${f[1/s]}$$は変化しません。
なぜなら、媒質と媒質の境界面で振動数が変わるとしたら、そこで波はぶつ切りになってしまいますがそんなことはありえない。強制的に同じ振動数を保つことになります。なので答えは
$${\fbox{ ア }}$$ 振動数
$${\fbox{ イ }}$$ 波長
$${v=f\lambda}$$
これがご存知、光の速度$${v[m/s]}$$・振動数$${f[1/s]}$$・波長$${\lambda[m]}$$の関係式です。
1波長の長さ$${\lambda=2[mm]}$$が1秒間に$${f=5}$$回通過したとしたら、1秒間に通過する波の長さは$${\lambda=2\times{5}=10[mm]}$$であり、これが波の速度になるのは割とピンときますよね。
$${v}$$:velocity
$${f}$$:frequency
$${\lambda}$$:lengthのlのギリシャ文字
が記号の由来です。
$${\fbox{ ウ }}$$ですが、「波長の短い光ほど屈折率が大き(い)」とあるので、答えは、より屈折している(i)となります。
問2
絶対屈折率の問題です。
絶対屈折率については、別の記事で詳述していますのでご覧ください。
まず用語。入射角$${i}$$と屈折角$${r}$$はそれぞれ、
incidence angle
reflection angle
が由来です。
この問題では、空気の絶対屈折率が1(真空と同じとみなす)、ダイヤモンドの絶対屈折率を$${n}$$とするとあるので、入射角$${i}$$と屈折角$${r}$$を用いて
$$
n_{空気→ダイヤモンド}=\dfrac{\sin{i}}{\sin{r}}=\dfrac{n_{ダイヤモンド}}{n_{空気}}=\dfrac{n}{1}
$$
これにより関係式は、
$${\fbox{ エ }}$$ $${\sin{i}=n\sin{r}}$$
$${\fbox{ オ }}$$の臨界角の問題は、ダイヤモンド→空気での屈折率で、空気に出るときに90度となる場合であるから、
$$
n_{ダイヤモンド→空気}=\dfrac{1}{n_{空気→ダイヤモンド}}=\dfrac{1}{n}=\dfrac{\sin{\theta_{c}}}{\sin{90^\circ}}={\sin{\theta_{c}}}
$$
よって、
$${\fbox{ オ }}$$ $${\sin{\theta_{c}}=\dfrac{1}{n}}$$
となります。
実は、$${\fbox{ オ }}$$は計算しなくても$${n}$$か$${1/n}$$かは一瞬で判別できます。
なぜならば、明らかに$${n>1}$$なので、1より大きくなることのない$${\sin\theta}$$が$${n}$$になるわけがありません。
ちなみに、$${\sin{\theta_{c}}}$$のcは、臨海角 critical angleが由来です。
問3
さてここから「ダイヤモンドが明るく輝く理由」となります。
「屈折率が大きいので、全反射になる光が多いことが理由だろうな」と推測できればしめたものです。


まずダイヤモンド。左下の$${0^\circ<{i}<{i_c}}$$のとき全反射か部分反射かを問うのが$${\fbox{ カ }}$$$${\fbox{ キ }}$$。
考え方:直角に近い角度では全反射はまず起こらないことを考えると、$${i_c}$$の左側$${\fbox{ カ }}$$の浅い角度が全反射エリアであると推測がつく。$${i_c}$$の右側$${\fbox{ キ }}$$$${90^\circ}$$までは部分反射。
ここで、下の赤丸部分が全反射エリアであることに気付こう。
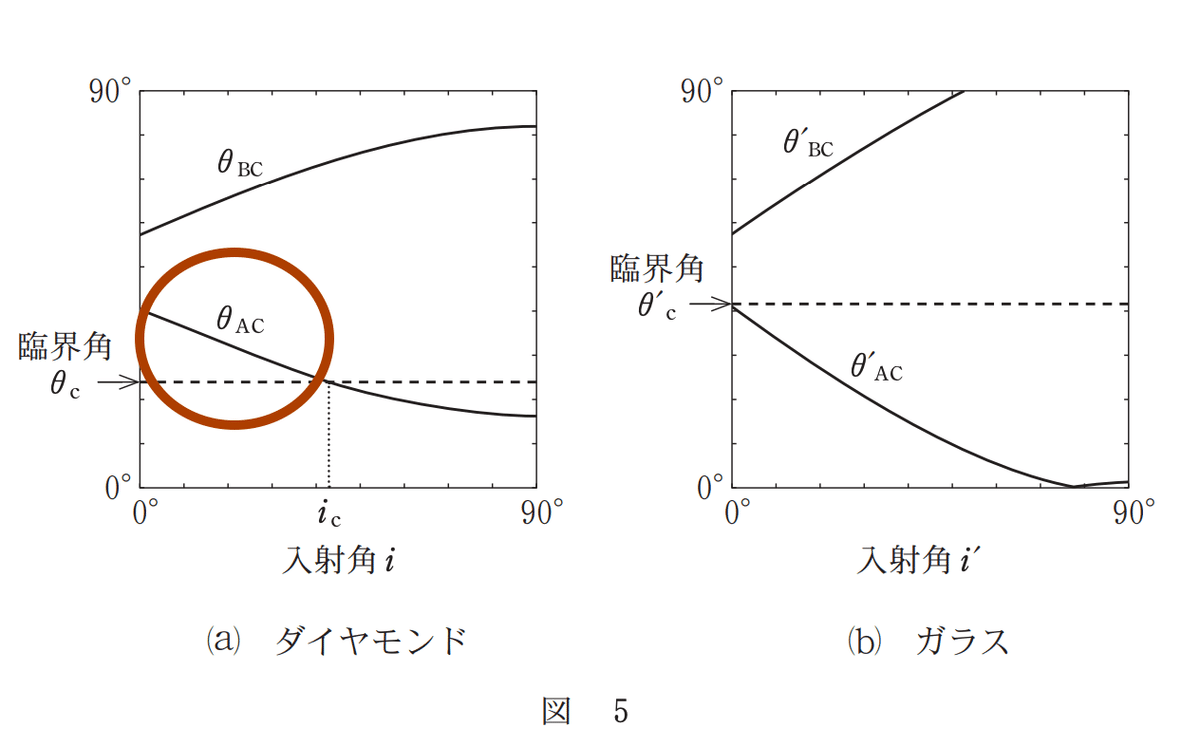
より改変
そうすると、右のガラスでは、赤丸部分が存在しないので、まるごと部分反射とわかります。$${\fbox{ ク }}$$は$${\textcircled{4}}$$。
$${\fbox{ ケ }}$$$${\fbox{ コ }}$$は従って$${\fbox{大きい}}$$$${\fbox{全反射}}$$となります。
やや深堀り
解答は以上ですが、グラフに関してなんだか釈然としないものが残ります。
下図は、角度や光量は正確ではありませんが、30°で入射した光がどう戻ってくるかを概念的に示しています。赤い線です。ダイヤモンドでは、左下のACで全反射が起こっている分、上方向に光が結構戻ってきます。一方ガラスでは、ACから光がダダ漏れで、ほとんど返ってきません。

また、ガラスのグラフの右上は線が消えています(赤丸)が、ここでは入射角をどうしようが最終的に右下BC面に平行か、逆方向の角度になるので、BC面での反射自体が起こらないようです。
ここまで、問題を素材にしての素人の考察でした。調べれば専門的な宝石用の光学があると思います。
ダイヤモンドのカットの角度や寸法比率は全反射に最適化されたものになっているようです。下記をご参考に。
