【統計学】標本の大きさ(サンプルサイズ)の決め方のまとめ
授業での質問:「母集団に対していくつ標本を取れば十分なのかがよくわかりません。どうやって決めるんですか」。
実務上大事な論点です。
改めて調べてみると、結論としては主に2通りの決め方があるようです。
許容誤差から逆算
検出力から逆算
用語確認
「標本数」と「標本の大きさ」
「大きさって何、採取した物の大小?」と思っても仕方がないと思います。
一般的な感覚とズレる統計用語の代表かなと思い、あらゆる記事・文献で言及されていますが、自分なりの解釈を加えて説明してみます。
標本数(サンプル数) 英語:number of samples 別名:群数 要するに:一回の標本採取を1群として、採集回数つまり群の数
標本の大きさ(サンプルサイズ) 英語:sample size 別名:「n数」 要するに:各群に属する個体数
わかりにくい。どちらも数には変わらないので。
例えば、発育状況の調査のために全国の30の各小学校から10人ずつ選んで調査した場合、標本数は30、各小学校の標本の大きさは10です。
日本語では数量を「サイズ」という習慣は余りありませんし、データを提供した小学生の誰それ君も標本と言える気がします。間違っているらしいが「標本数=300」とされても日本語的には違和感がありません(個人の感想)。
翻訳する時に「標本群数」「各標本個数」とでもしてくれれば良かったのにと思いますが、まあ、仕方ない。慣れましょう。
「信頼区間」と「信頼係数」
標本平均$${\bar{x}}$$は、標本が母集団の一部であるという宿命によりブレます。それが標本平均の分布です。
$$
{\bar{x} \sim N(\mu,\sigma^2/n) }
$$
標本平均は母平均$${\mu}$$の周りで、母分散$${\sigma^2}$$を標本の大きさ$${n}$$で割った分散の大きさでブレる訳です。
ここで、標準正規分布表に準えて検定するため、この標本平均の分布を翻訳(標準化)して、無理やり平均ゼロ、分散1に持っていくために、$${\bar{x} }$$を
$$
z=\dfrac{\bar{x}-\mu}{\sigma / \sqrt{n}} \sim N(0,1)
$$
と変数変換してあげます。
分母の$${\sigma / \sqrt{n}}$$は、標本平均の分散のルート、つまり標本平均の標準偏差であり、これを標準誤差(standard error: SE)と言います。
これで、標準正規分布を利用する準備が整いました。
さて、標本を使って母平均をピンポイントで当てることは不可能であり、ある程度のブレは覚悟しなくてはならないことは述べました。実は、唯一ピンポイントで当てる方法はあります。全数調査です。しかし、それは最早標本ではありません。
しかし、観測を何度も繰り返した場合に一定の確率でその中に母平均が収まる範囲を求めることは可能です。その設定する確率を信頼係数(confidence coefficient)といい、通常は95%とされます。
標準正規分布を使うと、確率95%の範囲が$${[-1.96,+1.96]}$$であることがわかります。
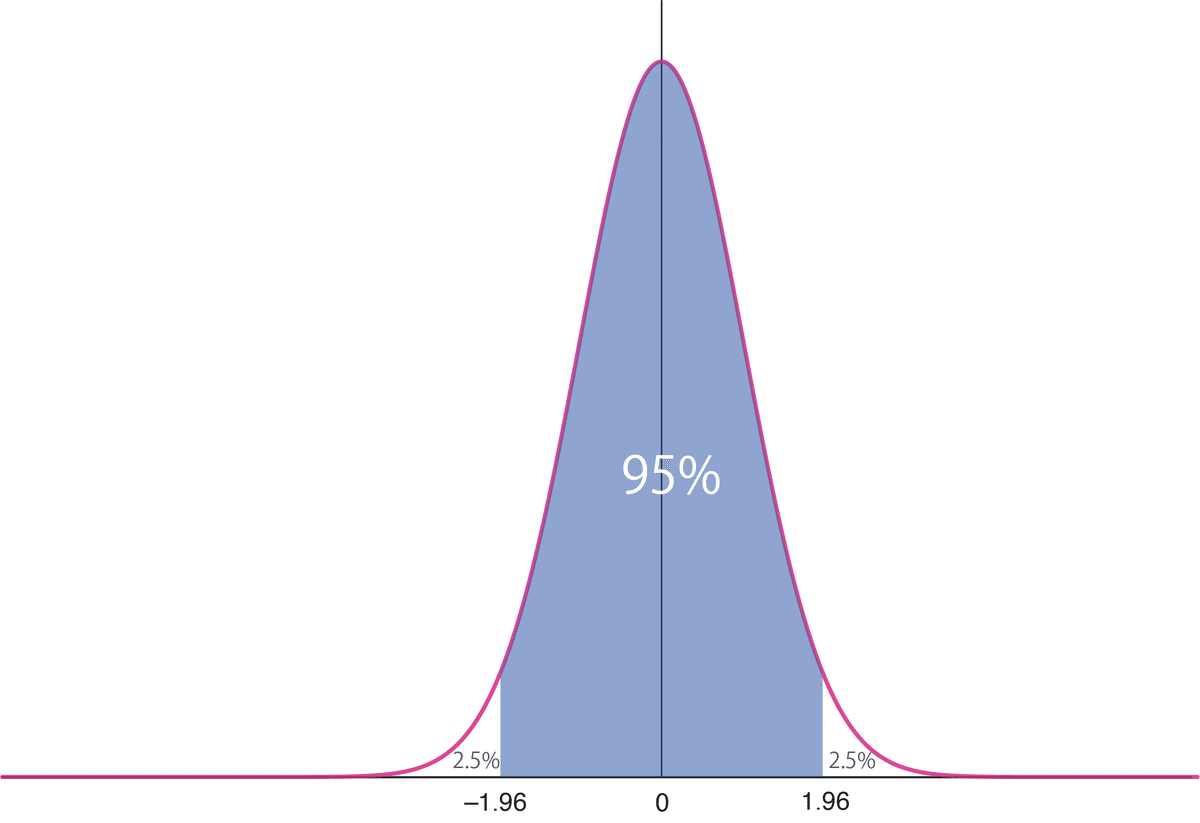
言い換えると、「$${z}$$がその中に95%の確率で収まる範囲は$${[-1.96,+1.96]}$$である」いうことになります。
$${z=\dfrac{\bar{x}-\mu}{\sigma / \sqrt{n}} }$$なので、その範囲を示すと、
$$
-1.96 \leq z=\dfrac{\bar{x}-\mu}{\sigma / \sqrt{n}} \leq +1.96
$$
主役を$${\mu}$$にするために変形すると、
$$
\bar{x}-1.96\dfrac{\sigma}{ \sqrt{n}} \leq \mu \leq \bar{x}+1.96\dfrac{\sigma}{ \sqrt{n}}
$$
ある観測値$${\bar{x}}$$が得られ、その値を上式に入れた場合、95%の確率で母平均$${\mu}$$がこの範囲にいる、と言うことになり、この範囲を95%信頼区間(confidence interval)と言います。
方法1:許容誤差から逆算
許容誤差とは
許容誤差とは、どれくらいの精度で結果を知りたいか、と言うことです。
例えば、ある県の10歳男子の平均身長を知りたい、と言うときに、誤差が±10cmもあったら無意味です。せめて±0.1cmくらいの精度がないと統計をとる意味がありません。
ここで、許容誤差を$${\pm d=\pm0.1}$$とし、観測結果から95%の確率で正しい母平均を算出するには、何人分のデータ(標本の大きさ)が必要になるでしょうか。
計算式
結論として、95%信頼区間の振り幅$${\pm 1.96 \dfrac{\sigma}{\sqrt{n}}}$$と許容誤差の振り幅が一致すれば良いので、
$$
1.96\dfrac{\sigma}{ \sqrt{n}} =d
$$
標本の大きさ$${n}$$を主役にすると、
$$
n=\left( \dfrac{1.96\sigma}{d} \right)^2
$$
未知の数値の取得と標本サイズの算出
ここで問題になるのは、標準偏差$${\sigma}$$は理論値からは求まらないことです。予備調査を行いおおよそのアテをつけるか、過去の類似の事例や文献のデータを利用するしかありません。
政府のe-Statの2019年、10歳男性のデータから、人数26人、平均身長138.1cm、標準偏差7.5が得られます。このデータから許容誤差を計算すると、
$$
SE={1.96\times\sigma / \sqrt{n}} = 7.5/\sqrt{26}\simeq 2.88
$$
と、3cm近い誤差を許容しているようですが、これ以外にデータがないのでそのままの標準偏差7.5を利用すると、
$$
n=\left( \dfrac{1.96 \times 7.5}{0.1} \right)^2=294
$$
となり、300人ほどのデータがないと±0.1cmの95%信頼区間は得られないと言うことになります。
方法2:検出力から逆算
検出力とは
検出力とは、ざっくり言うと、
実際は対立仮説が正しい(帰無仮説を棄却する)時に、間違って第二種過誤(消費者危険)を起こさず、ちゃんと対立仮説が正しいと検出(判断)できる確率
のことです。図で見る方が分かりやすいでしょう。
なお、この図は、標準化済みです。
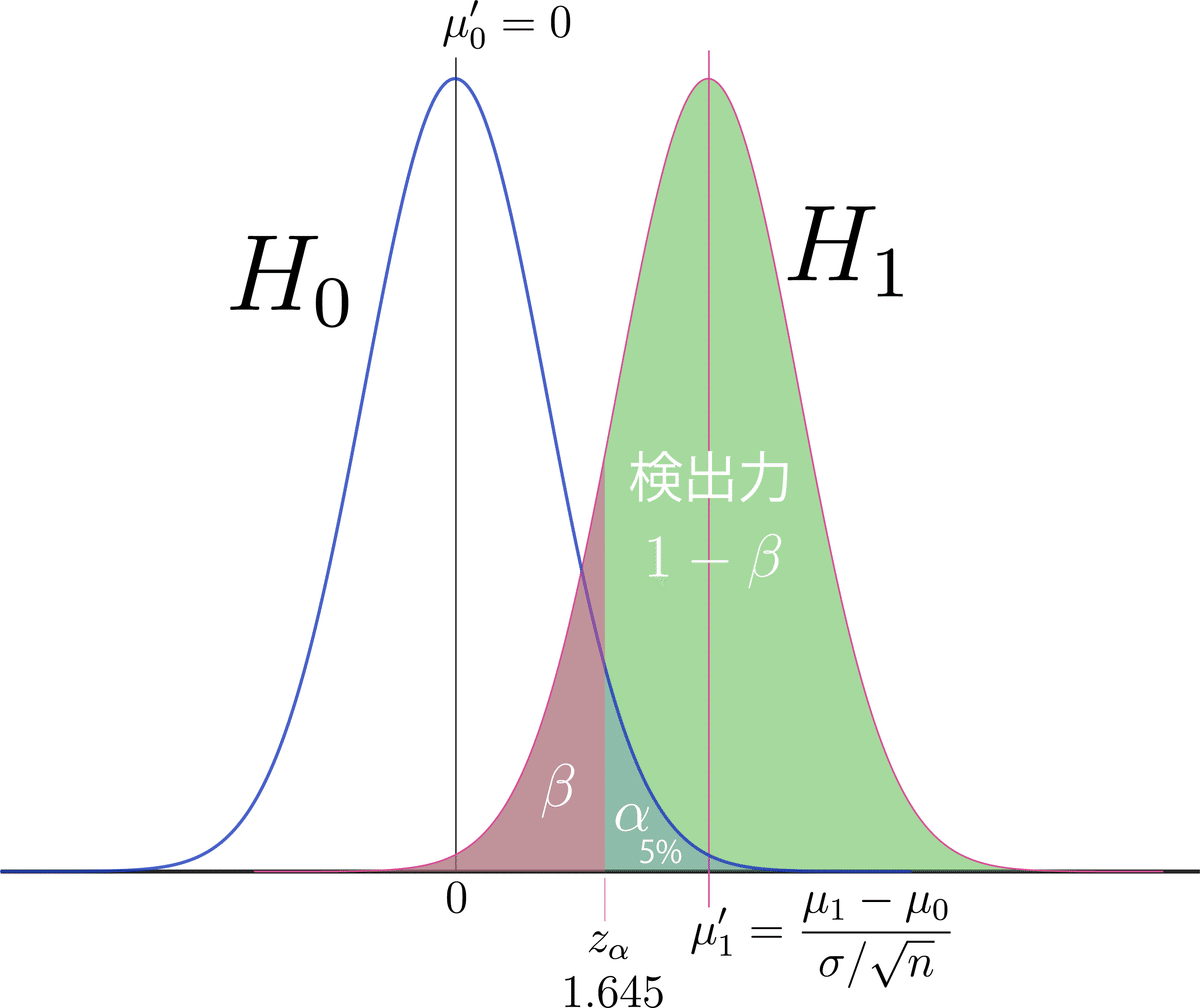
nが大きいと、検出力は上がります。
有意水準$${\alpha}$$を小さくすると、検出力は下がります。
標本サイズの算出
通常、検出力は80%が目安と言われています。
このときの$${\beta}$$の大きさは、標準正規分布の中心ゼロから$${z_\alpha-\mu'}$$だけ離れた値の上側確率であり、80%であれば$${z_\alpha-\mu'=0.8416}$$です。
$${n}$$の算出には、標準偏差$${\sigma}$$、想定される対立仮説の平均値$${\mu_0}$$などが必要ですが、これも、予備調査を行ったり文献から調達したりすることになります。
