【統計学】仮説検定の基本中の基本

2023年1月14日 05:55

　統計学の仮説検定を勉強すると、帰無仮説・対立仮説、z検定・t検定・母比率検定、母平均・母分散が既知・未知、等しい・等しくない、そして2標本問題の対応のある・なし、とまあ初心者が迷子になるようにしているのかと疑ってしまうような、初学者の行手を阻むような語感の用語と大技が次々と繰り出されて来ます。統計学に通じている人には当たり前の事なのでしょうけど、初心者からすると慣れない数式の上に聞いたこともない単語が並ぶだけで目が虚ろになること間違いなしです。

　当方の仕事は、迷子にならないよう手を引き、気がつくと目が虚ろになった生徒を引き戻し、なんとか基本のイメージを授けることと自負しています。

　上の色々な検定手法は、ド基本であるz検定の変種（様々な修正を施したもの）と割り切り、この回では、とにかくz検定の基本を「なんだ、そんなことか」と思ってもらうことを主眼に構成します。

仮説検定の予備知識

正規分布

　統計学の王様、正規分布について簡単に復習と確認を行います。

$$
f(x)=\dfrac{1}{\sqrt{2\pi\sigma^2}} \exp \left\{ -\dfrac{(x-\mu)^2}{2 \sigma^2} \right\}
$$

　これが確率密度関数（要するに上軸が確率となる関数）$${f(x)}$$です。
　母数（その形を決定する変数）が平均と分散なので、$${N(\mu,\sigma^2)}$$と表されます。
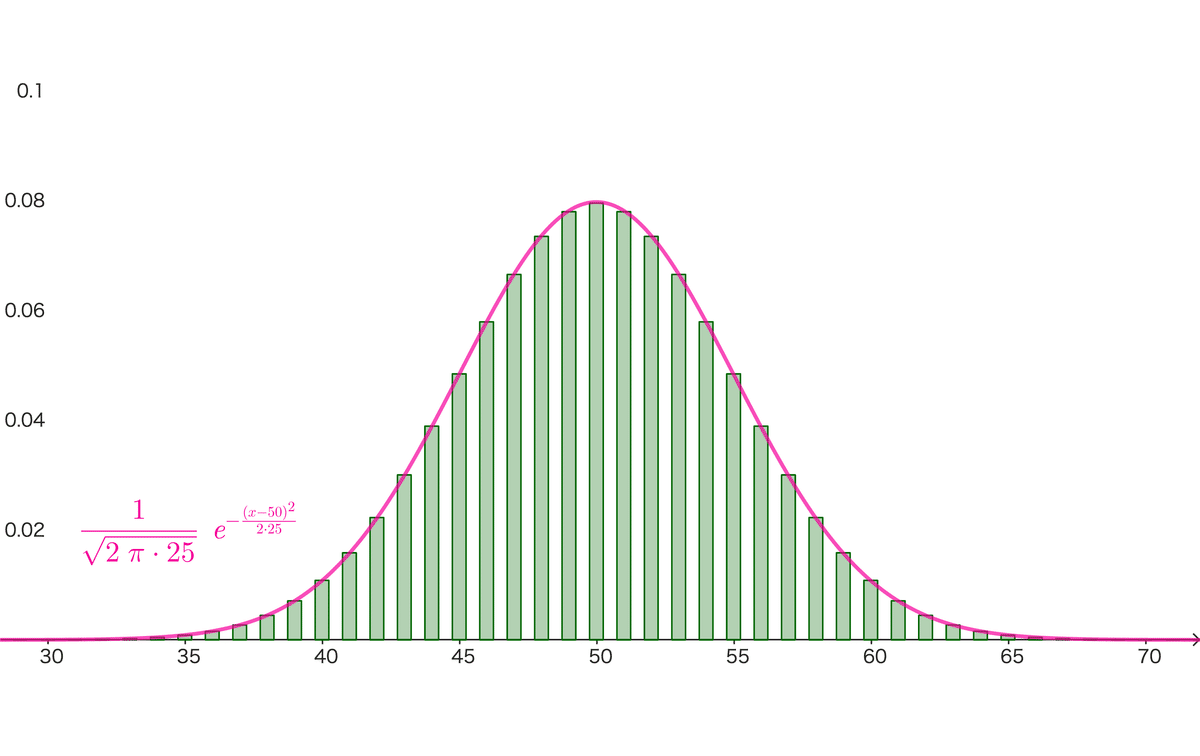
　典型的な例としては、コイン投げ（二項分布）やサイコロ投げ（多項分布）をメチャクチャ頑張れば、正規分布にどんどん近づきます。
　例えば、コインを100回投げたデータ（$${\mu=50,\ \sigma^2=25}$$）は以下の通り。ポイントは、コイン投げのような離散データであっても、平均と分散さえ分かれば、それを上のややこしそうな式に代入すれば大体同じ形になるという事実です。

標準化得点

　明日（執筆時は2023年1月13日）、大学入学共通テストが始まります。
　配点は、国語200点、理科は1科目（例えば物理）100点だそうです。
　さて、結果、平均点が国語97点、理科63点だったとして、国語の方が高得点だから問題が簡単だった、なんて判断するのは馬鹿げてますよね。
　また、テストというのは毎回得点のばらつきが異なるので、試験結果全体の中で自分の位置を確認したくても、点数が高い低いだけでは判断できません。
　そこで、標準化得点という考え方が登場します。

$$
Z=\dfrac{X-\mu}{\sigma}
$$

　標準化得点とは、実際の得点$${X}$$と平均点$${\mu}$$との差（偏差）を標準偏差$${\sigma}$$で割ったものです。この操作により、元々正規分布に従っているが平均や偏差がまちまちであったデータを、平均$${0}$$、分散$${1}$$に無理やり合わせる事ができます。

　尚、テスト等で使われるいわゆる「偏差値」は、平均50、分散10にしたものです。恐らくテストっぽい雰囲気を出すのと、「あなたの点数マイナス20点」と言われて気分を害されるのを避けるためにこうしているのでろうと邪推しています。

演習　次のデータを標準化し、標準化後の平均と分散を確認せよ。

$${ 0,1,1,1,2,2,2,3}$$（コイン3回投げ得点）
$${ 0,1,1,1,1,2,2,2,2,2,2,3,3,3,3,4}$$（コイン4回投げ得点）

標準正規分布

　正規分布$${N(\mu,\sigma^2)}$$を標準化（$${\mu=0,\ \sigma^2=1}$$）したものを標準正規分布(standard normal distribution）といい、$${N(0,1)}$$と表します。その確率密度関数は、正規分布の式に$${\mu=0,\ \sigma^2=1}$$を代入して

$$
\psi(z)=\dfrac{1}{2\pi} \exp(-\dfrac{z^2}{2})
$$

となります。だいぶスッキリしましたね。グラフはこのようになります。

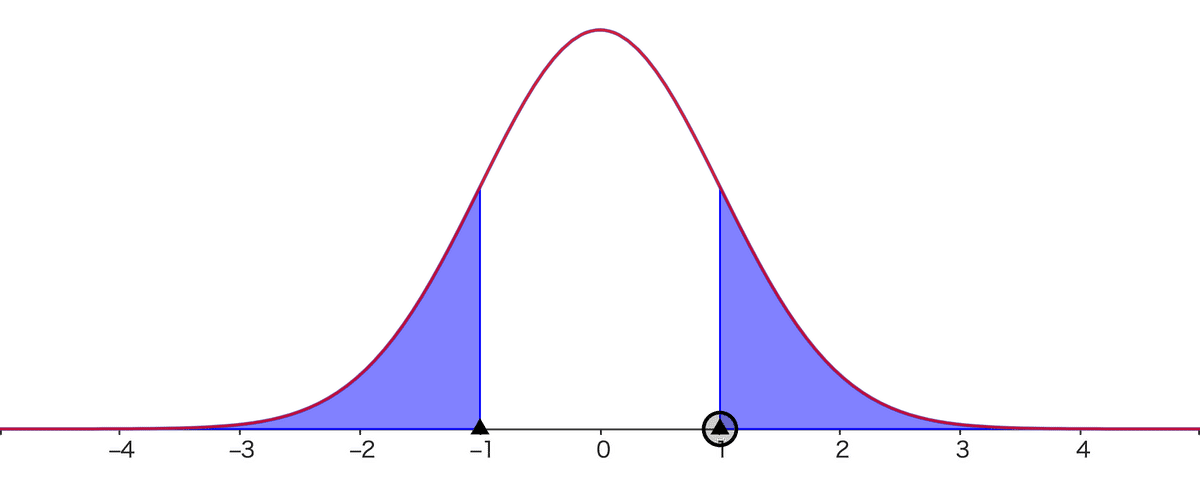
　グラフでは、$${\pm 1\sigma}$$範囲を示しています。外側の青い部分は片側約16%、両側合わせて約32%になります。後述する標準正規分布表から得られます。
　$${\sigma=\pm 1}$$なので、$${\pm 2=\pm 2\sigma}$$、以下同様です。
　品質管理で有名なシックスシグマ（3.4ppm）に相当するのは、実は$${4.5\sigma}$$であり、$${6\sigma}$$ではありません。これは、平均値の一般的な揺れ$${1.5\sigma}$$を加味しても尚3.4ppmが実現される数値を設定しているということです。

https://ja.wikipedia.org/wiki/シックス・シグマ

　実は今後、正規分布に従う様々なデータを、まずは標準化して、標準正規分布を用いて判断していくことになります。
　別にわざわざ標準化しなくてもいいのではないかと思うかも知れませんが、理由があります。
　実はこの関数には原始関数（不定積分）が存在しないので、普通に定積分を計算することができません。なぜか$${-\infty \sim +\infty}$$の積分だけはできますが。
　そのため、標準正規分布のある範囲の値（面積）を求めたい時は、統計学の本には必ず巻末付録についてくる標準正規分布表を参照して近い値を探すことになります。または、今なら統計ソフトや表計算ソフトを操作すれば勝手にデータを出してくれます。

　じゃあ、その標準正規分布表の値はどうやって計算したのか？とお考えの向きもあろうかと思いますが、これは、関数をマクローリン展開という方法で無理やり多項式（$${ax+bx^2+cx^3+,\cdots}$$みたいな形にして気合いで計算します。無限の足し算なのでいいぐらいのところまで力技で計算することになりますが、毎回こんなことをしていると日が暮れるので、超メジャーな標準正規分布等については数字が前もって用意してある、という仕組みです。

仮説検定の基本の基本：二項検定と考え方の肝

【問】滅多に起こらない稀な出来事が起こる確率を5%以下と前もって設定し、それが起こった場合は普通ではないと判断することにします。

　サイコロを5回振りました。次の結果が得られた場合、サイコロは普通ではない(イカサマ)と判断できるでしょうか。

4回偶数が出た
4回連続偶数が出た
5回とも偶数が出た

　さて、これらは普通に確率が計算できます。
　我々は、前もって、5%以下が「偶然起こらないレアケース」と判断すると約束しました。なので、上の確率が5%以下であれば「イカサマ」と判断されます。
　但し、注意が必要なのは、「4回偶数が出た」場合の確率は、「4回偶数、1回奇数が出た」場合とそれよりレアな「5回とも偶数が出た」確率を足し合わせないとフェアではないということです。
　もしこれに「5回とも偶数が出た」確率を足さなかったばかりに5%を切ってレア判定が出たとしたら、単に「4回偶数が出た」という特定の場合の確率をピンポイントで切り出して判定することになるからです。それが許されるなら、「2回6が出る確率=1/36」で、5%を下回ってしまいます。

　大まかな考え方はこれだけです。二者択一の場合のこのような検定を二項検定といいます。

仮説検定の基本：z検定

　次に、連続確率（二項検定のように飛び飛びの値を取らない確率）の仮説検定の基本であるz検定について説明します。

仮説検定の考え方

　どの検定にも通じる考え方です。
　ざっくり言うと、標本で得られた統計量（平均や分散など）が、

許される揺れの範囲（まあ、そんなこともあるよねくらい）→別に何もない
それを超えてレアな数値を叩き出した（おっと、これはちょっとあり得ない数字だ）→何か意味がある

　例えば、ある薬を飲んだ人たちとそうでない人たちで血圧を調べて差が出たとき、その差が偶然の揺れの範囲かどうかを判定し、範囲を外れるほど大きな差が出たらその薬には効果あり、みたいなことです。
　もちろん色んなバリエーションがありますが、基本的にはレアかどうか、レアならたまたまではないので何かあるぞ、そんな感じです。

z検定とは

　まず、流れを示します。

【母集団・標本設定】母集団から標本（母集団の一部）を取り出す。母集団の平均$${\mu_0}$$と分散$${\sigma^2}$$が既知（数値がはっきり分かっている）で、何もなければどの標本も$${N(\mu_0,\sigma^2)}$$に従うはずであることが前提。
【仮説設定】帰無仮説$${H_0:\mu=\mu_0}$$（平均の違いは偶然の範囲内なので特に意味はない）と対立仮説$${H_1:\mu \ne \mu_0}$$（偶然では済まないほど珍しいのでこの標本は母集団とは違うものだ）を定める。
【検定統計量設定】検定統計量として、標本平均$${\bar{x}}$$を採用する。標本平均は、帰無仮説$${H_0:\mu=\mu_0}$$が正しければ、母平均と何ら変わらないはず。一方、標本平均には揺れがあり、標本平均の分散は、$${\sigma^2/n}$$なので、$${\bar{x}}$$は$${N(\mu_0,\sigma^2/n)}$$に従うはず。
【有意水準設定】有意水準（通常$${\alpha=0.05}$$）を定める。5%以下の発生確率のものは滅多に起こらないので、偶然ではなく何らかの意味があると考える。慎重を期する場合は、$${\alpha=0.01}$$とする流儀もある。
【両側・片側設定】両側検定か片側検定かを定める（今回は両側検定を採用）。大小どちらでも意味がある場合は両側、どちらかでいい時は片側。
【棄却域の最小値取得】標準正規分布の上側確率（滅多に起こらないことが起こる範囲）が$${ P(|z|\geq \beta)=0.025}$$となる$${\beta=1.96}$$を見つける。両側を合わせた確率は$${0.025 \times 2 = 0.05}$$。
【棄却域設定】棄却域($${H_0}$$を棄却し$${H_1}$$を採用する範囲)を設定。標準化した$${\bar{x}}$$を用い、$${\dfrac{|\bar{x}-\mu_0|}{ \sigma/ \sqrt{n}} \geq 1.96}$$を設定する。
【検定】標本平均$${\bar{x}}$$が棄却域の範囲内かどうかを判断する。範囲内なら帰無仮説$${H_0}$$を棄却し対立仮説$${H_1}$$を採用（つまり有意）、そうでなければ受容（判断保留。帰無仮説$${H_0}$$を積極的に否定するまでの材料はないということ）。

　いわゆる「P-値」は、「統計量がその観測値（ここでは標本平均$${\bar{x}}$$
）か、それより極端な値をとる確率」と定義され、棄却域と似ているが異なっている。
　例えば棄却域が5%であっても、観測値又はそれより極端な値をとる確率（を足し合わせたもの）が3%であれば、P-値は3%となる。
　両側検定の場合のP-値は、単純に2倍するか、観測値より小さい確率の事象を足し合わせるという二つの流儀がありやや曖昧である。

　レアケースではあるが$${H_0}$$が実は正しい（不良品ではない）のにたまたま5%以下で棄却することを第1種過誤（生産者危険）、逆に、$${H_0}$$が間違い（不良品）なのに棄却しないことを第2種過誤（消費者危険）という。

検定してみよう

　ネジを作る工場のラインでの抜き取り調査を行います。

1.【母集団・標本設定】
　母集団：これまでの経験から、以下の統計値が得られているものとします。
　　平均長さ(cm)$${\mu_0=1}$$、標準偏差$${\sigma=0.03}$$

　標本：検査の結果：標本数$${n=16}$$、標本平均$${\bar{x}=1.015}$$

2.【仮説設定】帰無仮説$${H_0:\mu=\mu_0}$$、対立仮説$${H_1:\mu \ne \mu_0}$$

3.【検定統計量設定】標本平均$${\bar{x}=1.015}$$を採用する。
　帰無仮説$${H_0:\mu=\mu_0}$$が正しければ、標本平均は母平均と何ら変わらないはずなので、$${N(\mu_0,\sigma^2/n)}$$に従うはず。

4.【有意水準設定】$${ \alpha=0.05 }$$

5.【両側・片側設定】長くても短くてもアウトなので、両側検定とする。

6.【棄却域の最小値取得】$${1.96}$$

7.【棄却域設定】 $${ z=\dfrac{|\bar{x}-\mu_0|}{ \sigma/ \sqrt{n}}}$$

8.【検定】棄却域に$${x}$$が入っているかどうかを確認し、$${H_0}$$を棄却あるいは受容を決定する。

結果はどうなりましか？

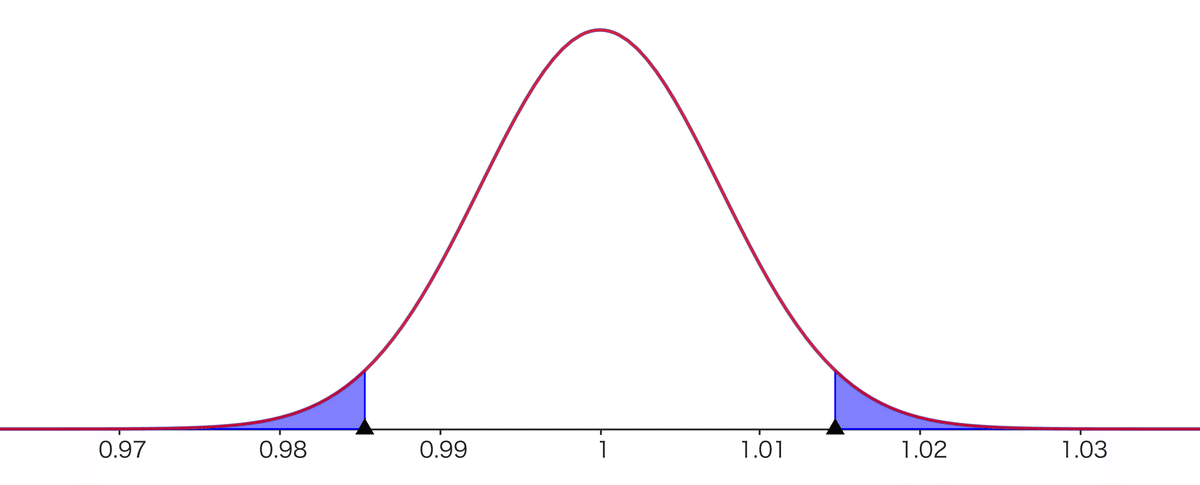
因みに、棄却域を長さに直したものを置いておきます。このグラフが、平均の揺れを表しています。

この記事が気に入ったらサポートをしてみませんか？