セル看護提供方式®による転倒・転落防止効果の検証
セル看護提供方式®とは
セル看護提供方式®の定義は、以下の内容です。
ナースの「動線」に着目し、改善手法を用い動線のムダを省き、「患者のそばで仕事が出来る=患者に関心を寄せる」を実現する看護サービス提供システムです。これは飯塚病院が開発した看護提供方式です。
これまでは、患者さんの処置が終了するとそばを離れ、スタッフステーションに戻って看護記録や情報交換のカンファレンス、ケアに必要な物品の準備などを行っていました。現在は、看護に必要な物品を積み込んだカートを活用し、できるだけ患者さんのそばを離れることなくケアが行えるようになりました。そのため、患者さんのことがよくわかるようになり、必要なケアの提供が可能となっています。
飯塚病院看護部HP
今回、セル看護提供方式®の転倒・転落防止効果を検証するため、介入前期間と介入後期間でで得られたデータの検定を行いました。
結果データ
共通項目
時間帯:日勤帯(8:30〜17:00)
対象:65歳以上の入院患者
期間:介入前:2019年度、介入後:2020年度
月別データ
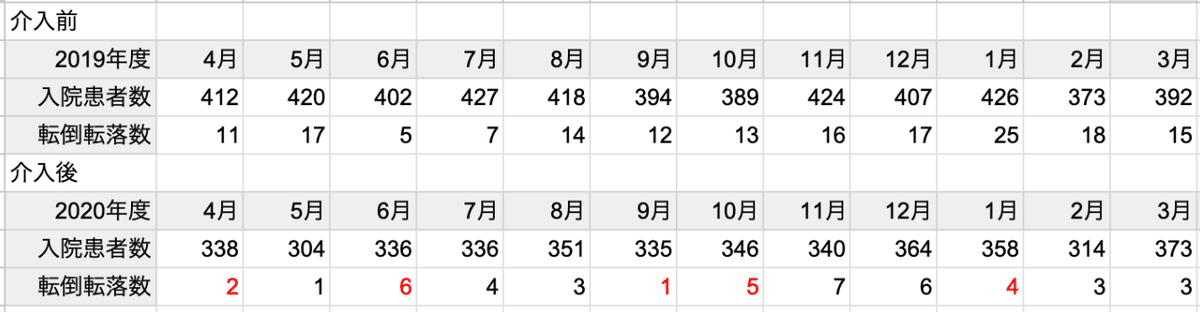
データの要約
介入前 転倒転落数170 なし4714 計4884 転倒転落率 3.48%
介入後 転倒転落数45 なし4050 計4095 転倒転落率 1.10%
独立性の検定
この検定は、二つの属性に対し、それぞれ複数の結果が得られたものを集計した分割表を利用します。
今回は、縦軸に介入前・介入後、横軸に転倒転落有り・無しとします。
表から計算したズレの値がカイ二乗分布に従うことを利用し、データが偶然の範囲かどうかを検定する流れとなります。
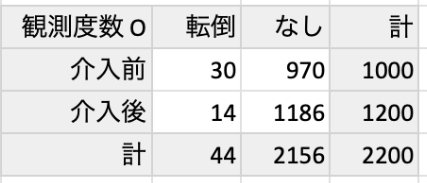
観測度数
実際に得られたデータを観測度数といいます(下記は練習用のモデルデータです)。

期待度数
両者に関係がない(帰無仮説$${H_0}$$:偶然の範囲)と仮定した場合のデータを期待度数$${E}$$といいます。
実際には、それぞれの観測度数を合計欄の比率で割り戻した数値となります。つまり、介入前と介入後で転倒転落の比率が変わらないようにします。
練習:空欄を埋めよ。

カイ二乗値の算出
観測度数$${O}$$が期待度数$${E}$$からどれだけズレているかを計算します。
ズレの計算は、それぞれ対応する項目において$${(O-E)^2/E}$$を計算し、足し合わせます。この値を$${\chi^2}$$値といいます。
練習:空欄を埋め、$${\chi^2}$$値を算出せよ。
尚、網掛けの行和・列和部分の合計値は必要ない。

別解:この計算は、以下の数値だけですぐに計算できることが分かっています。

$$
\chi^2=\dfrac{N(ad-bc)^2}{pqmn}
$$
練習:別解の方法で$${\chi^2}$$値を算出せよ。
モデルデータの検定
この$${\chi^2}$$値は、$${\chi^2}$$分布に従うことが分かっています。
今回は、自由度$${df=(2-1)\times (2-1)=1}$$、つまり自由度1の$${\chi^2}$$分布に従います。
$${\chi^2 \leq 3.8415}$$の細い部分が5%の棄却区間であり、観測値から計算した$${\chi^2}$$がこの値を超えるとレアケースと解釈されます。つまり、帰無仮説$${H_0}$$が正しいと仮定した場合には5%以下の確率でしか起こらない事象が観測された訳なので、これは偶然ではなく有意であるとされます。
練習:このモデルデータを検定せよ。

$${\chi^2}$$分布については、拙文で少し解説しています。
$${(O-E)^2/E}$$を合計したものがなぜ$${\chi^2}$$分布に従うのかの証明は、高度な線形代数を用いたものもありますが、こちらの記事によると、ほとんど説明がされていないそうです。
http://joe.bayesnet.org/?p=4895
この記事の著者の鈴木譲氏による証明が、最もシンプルで明快と個人的に思います。後日引用して紹介したいと思います。
http://joe.bayesnet.org/wp-content/uploads/2017/05/2017-5-25-1.pdf
少しは頭を使ったらどうか: 分割表の適合度検定の証明。 投稿者: 鈴木 譲 | 2017年5月26日
実際のデータの検定
練習:以下の実際のデータを検定せよ。

母比率検定(参考)
介入前 転倒転落率 3.48%
介入後 転倒転落率 1.10%
母比率の検定は、得られた比率の差が正規分布に従うことを利用して行います。
実際のデータを用いて母比率の検定も行ったところ、ほぼ同じ結果が得られました。別途機会を見て解説します。
皆様。長い間お越しいただきありがとうございました。引き続きよろしくお願いします。
