
【統計学】カイ二乗分布。なぜこんな形?手作業でやってみた。
独立に標準正規分布に従う k 個の確率変数$${X_1, …, X_k}$$ をとる。
このとき、統計量
$${ Z=\sum _{i=1}^{k}{X_{i}}^{2} }$$
の従う分布のことを自由度 k のカイ二乗分布と呼ぶ。
この説明に「こんなグラフになります」と見せて、平均が自由度と一致、分散は自由度の2倍。これで大概の教科書のカイ二乗分布の説明は終わり。

ふーん、そうなるのか。なるほど。山が低くなりつつ右に移動するのね…
ちょっと待て。
…皆さん、どうしてこんな形になるのか、納得していますか?
少なくとも私は、この説明だけでは全く分かりません(でした)。
$${X^2}$$の確率密度?普通$${X}$$でやるところを、例えば$${X=3}$$なら$${X=9}$$のところを読みに行くのか?それとも、$${X=3}$$の確率を$${X=9}$$によいしょと持っていくのか?そこからピンとこない。
この、統計学の割と早い段階で出てくるカイ二乗分布。多分、なぜこうなるか分からずに使っている方が多いと思い(そうでなければ申し訳ない)、正規分布から手作業で再現してみました。
ミニチュアを用意
二項分布B(4,1/2)を用意
まず、$${X}$$は正規分布に従うとのこと。そして正規分布のミニチュアとして二項分布が手頃であろう。離散分布と連続分布の違いはあるものの、挙動は同じに違いない。きっとそうだ。
そこで、このコイン4回投げ(表1点裏0点の得点の期待値)$${B(4,1/2)}$$データ16個を用意しました(4回にしたのは、実は3回だと計算がめんどくさいからです)。
個数が度数そのもので、度数を16で割ったものが確率となります。泥臭いやり方ですが、これしか思いつかない。
$${X=\{\underbrace{0}_{1個}, \underbrace{1,1,1,1}_{4個}\ \underbrace{2,2,2,2,2,2}_{6個},\ \underbrace{3,3,3,3}_{4個} ,\underbrace{4}_{1個} \} }$$
標準化
このデータを標準化しましょう。
平均は$${\mu=np=2}$$、分散は$${\sigma^2=np(1-p)=1}$$なので、正規化後のデータ$${Z}$$(以下、Wikipediaの記号とは少々異なりますのでご注意ください。)は$${(X-\mu)/\sigma}$$を用いて、
$${Z_1=\{\underbrace{-2}_{1個}, \underbrace{-1,-1,-1,-1}_{4個}\ \underbrace{0,0,0,0,0,0}_{6個},\ \underbrace{1,1,1,1}_{4個} ,\underbrace{2}_{1個} \} }$$
となります。念の為確認しても明らかに平均$${0}$$、分散$${1}$$で正規化されています。
自由度1のカイ二乗分布を作る
さて、この$${Z_1}$$を用いて$${Z_1^2}$$を作れば、自由度1のカイ二乗分布($${\chi^2 (1)}$$)になるはず。やってみよう。
$$
\begin{align*}
W&=Z_1^2=\{4,1,1,1,1,0,0,0,0,0,0,1,1,1,1,4 \} \\
&=\{\underbrace{0,0,0,0,0,0}_{6個},\underbrace{1,1,1,1,1,1,1,1}_{8個},\underbrace{4,4}_{2個} \}
\end{align*}
$$
こういう解釈で良いのか、やや不安は残るが、勇気を出して進めてみよう。
まず教科書には「自由度$${n}$$の$${\chi^2}$$分布の期待値は$${E[W]=n}$$、分散は$${V[W]=2n}$$とある。今回自由度は$${1}$$なので$${ E[W]=1, \ V[W]=2 }$$となるはず。果たして、
$$
\begin{align*}
E[W]&=\dfrac{1}{16} \sum_{i=1}^{16} W_i =\dfrac{16}{16}=1\\
V[W]&=\dfrac{1}{16} \sum_{i=1}^{16} W_{i}^{2}-E[W]^2=\dfrac{0^2 \times 6 + 1^2\times 8+4^2 \times 2}{16}-1=\dfrac{3}{2}
\end{align*}
$$
平均はバッチリだが、分散が$${2}$$にならない。恐らくこれは離散分布のせいで少し小さいのだろう。とりあえず放置して、グラフを描いてみよう。確率は、度数を16で割れば良いので、$${0,1,4}$$それぞれ$${6/16,8/16,2/16}$$となる。

本物と重ねてみよう。

なんか違う。不安だ。
しかし、ここでやめる訳には当然行かない。
シミュレーション
自由度2のカイ二乗分布を作る
さて本番。$${Z_2^2}$$を用意しよう。
$${Z_1}$$と$${Z_2}$$は「独立」とのこと、その意味するところは何だろうか。
コインを4回投げた1回目の、出た目を標準化して二乗したのが$${Z_1^2}$$。
コインを4回投げた2回目の、出た目を標準化して二乗したのが$${Z_2^2}$$。
得られる数値は、どちらも$${\{ 0,1,4\}}$$の3種類で、頻度はそれぞれ$${\{ 6,8,2\}}$$。
独立であるということは、2回の結果について、万遍なく組み合わせが発生するということであろう。ならば、$${Z_1^2}$$と$${Z_2^2}$$を足し合わせた結果は、
$$
\{0+0=0\},\{0+1=1\},\{0+4=4\}\\
\{1+0=1\},\{1+1=2\},\{1+4=5\}\\
\{4+0=4\},\{4+1=5\},\{4+4=8\}
$$
となり、結局、$${ W=\{ 0,1,2,4,5,8\}}$$の6通りの結果が、それぞれの確率(頻度)に応じて得られる、ということになるはずだ。図にしてみよう。

世間ではこれを同時確率分布(joint probability distribution)とか同時分布とかいうらしい。要するに万遍なく組み合わせる、それだけのことですね。
上の結果をまとめると、
$$
\left[\begin{array}{rrrrrrr}
Z_1^2+Z_2^2= & 0 & 1&2&4&5&8\\
p= & 36 & 96 & 64 & 24 & 32&4 \\
\end{array}
\right]
$$
さて、まだ数字が凸凹しているが、描画してみよう。今回は本物込みで。

おっと、少しは近づいたような気がする。
自由度3のカイ二乗分布を作る
同じ容量で、3つ目を組み合わせます。
本来は3次元で表されるものですが、流石に複雑過ぎるので、自由度2でまとめたものと、新たな$${Z_3^2}$$を組み合わせます。

結果をまとめるとこの表のようになります。
$$
\left[\begin{array}{rrrrrrrrrrr}
Z_1^2+Z_2^2+Z_3^2= &0&1&2&3&4&5&6&8&9&12\\
p= &216&864&1152&512&216&576&384&72&96&8 \\
\end{array}
\right]
$$
さて、今度はどうだろうか。

うーん、近づいているのか。悪くはない感じはする。
自由度4のカイ二乗分布を作る
はい。要領は同じです。

$$
\left[\begin{array}{rrrrrrrrrrrrrrr}
Z_1^2+Z_2^2+Z_3^2+Z_4^2= &0&1&2&3&4&5&6&7&8&9&10&12&13&16\\
p=&1296&6912&13824&12288&5824&6912&9216&4096&864&2304&1536&192&256&16 \\
\end{array}
\right]
$$
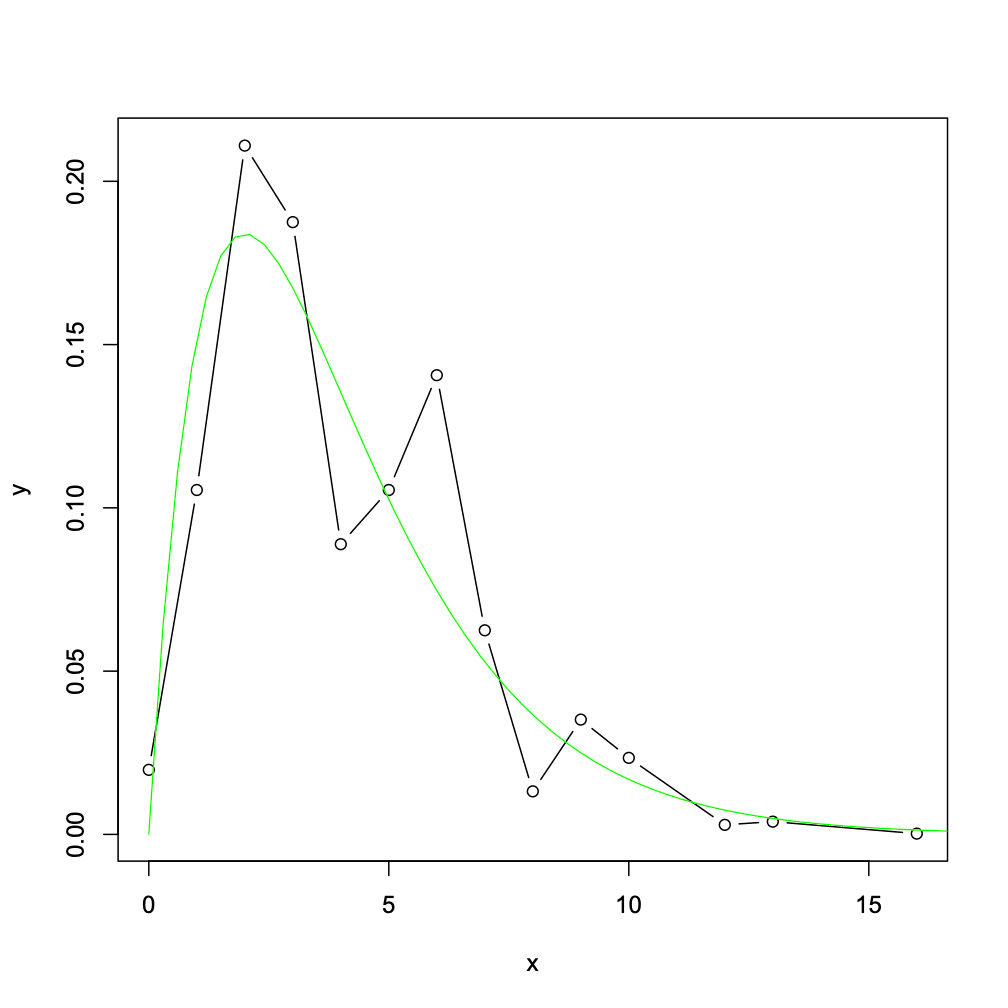
前とそんなに変わらないが、少し近づいたようだ。
しかし少なくとも、離れてはいないし、最大値や尻尾も大体押さえている。
自由度5のカイ二乗分布ではどうだ
同様に自由度5。結果のみを示します。

悪くはない。恐らくこれを繰り返せばもっと近づく(に違いない)。
結論
離散的なデータからなのでどうしても初めは凸凹しますが、新たな$${Z^2}$$が加わることでどんどん隙間が埋められていきました。
山のてっぺんが移動することも確認できました。要するに、初め大きかった0の度数は、新たなメンバーによりどんどん上に引き上げられ、残るのはほんのわずかになっていっていくようです。
とにかくも、考え方は合っているようです。しかし疲れた。
