
アロエヨーグルトの日
まえがき
12月10日は、アロエヨーグルトの日とされている。
ヨーグルトについては別で書くとして、今回は、上記のnoteで宿題となっているエイダ・ラブレスについて、書いてみたいと思う。
エイダ・ラブレス
エイダ・ラブレスは、19世紀イギリスが生んだ卓越した数学者であり、世界最初のコンピュータープログラマーとして歴史に名を残した人物である。1815年12月10日、ロマン派の詩人として名高いジョージ・ゴードン・バイロンの一人娘として生を受けたが、その運命は波乱に満ちたものとなった。
生後わずか1ヶ月で父との別離を経験した彼女は、母アナベラの厳格な教育方針の下で育てられることとなる。この教育は、後の彼女の数学的才能の開花に重要な礎を築いた。母アナベラは、当時としては珍しく、娘に対して数学や科学の教育を重視した。これは、詩人であった父バイロンの芸術的な影響力を懸念してのことだったとも言われている。
エイダの人生における転機は、18歳の時に出会ったチャールズ・バベッジの階差機関との邂逅である。この機械式計算機との出会いは、彼女の知的好奇心を大いに刺激した。その後、バベッジの解析機関に関する論文の翻訳を手掛けた際、彼女は単なる翻訳以上の貢献をなした。独自の注釈には、現代のプログラミングの基礎となる概念が多数含まれていた。
特筆すべきは、エイダが当時としては革新的な発想で、コンピュータが純粋な計算を超えた可能性を持つと考えていたことである。彼女は、機械が音楽を作曲できる可能性を示唆し、これは現代のコンピュータ音楽の先駆的な予見となった。さらに、ベルヌーイ数を計算するプログラムを考案し、現代のプログラミングで使用される基本的な制御構造の多くを先取りしていた。
しかし、その輝かしい知性は、1852年11月27日、わずか36歳という若さで消えることとなる。子宮癌に冒された彼女は、当時の医学の限界により、誤った治療法である瀉血を受け、これが死期を早める結果となった。皮肉にも、これは父バイロンと同じ年齢での死であり、同じ治療法による悲劇であった。
エイダの先見性と功績は、現代において広く認知されている。毎年10月の第2火曜日は「エイダ・ラブレスの日」として祝われ、1983年には米国国防総省が彼女の名を冠したプログラミング言語「Ada」を開発した。このプログラミング言語は、現在でも特に組み込みシステムや航空宇宙分野で重宝されている。
エイダ・ラブレスの生涯は、19世紀という時代の制約の中で、女性として数学やコンピューティングの分野で先駆的な業績を残した稀有な例として、現代のコンピュータサイエンスの礎を築いた重要な人物である。彼女の洞察と先見性は、現代のデジタル時代を予見していたと言っても過言ではない。
ベルヌーイ数
ベルヌーイ数については、
上記のnoteで書いた。多少補足をしておくとすれば、
ベルヌーイ数は、数学の歴史において特筆すべき数列であり、その発見と応用は数論の発展に大きな影響を与えた。一見複雑に見えるこの数列だが、その本質は意外にもシンプルな原理に基づいている。
まず、ベルヌーイ数の定義を直感的に理解するため、指数関数の逆数に近い関数 x/(e^x-1) を考える。この関数をテイラー展開すると現れる係数こそが、ベルヌーイ数である。この数列は非常に興味深い性質を持っており、すべての項が有理数となる。最初の項 B₀ は1、次の項 B₁ は -1/2 となり、以降の項は規則性を持って並んでいく。
特に注目すべきは、B₁ 以降の奇数番目の項がすべて0になるという驚くべき性質である。これは単なる偶然ではなく、数学的な必然性から生まれる結果である。また、偶数番目の項は、その大きさが急速に増大しながら、正負が交互に現れるという特徴を持つ。
歴史的には、この数列が18世紀初頭に、東洋と西洋で独立に発見されたことは非常に興味深い。日本の和算家である関孝和が1712年に『括要算法』で記述し、翌年にスイスの数学者ヤコブ・ベルヌーイが『推測術』で発表した。この時代、東西の数学者たちが、地理的な隔たりを超えて同じ数学的真理にたどり着いたことは、数学の普遍性を示す好例である。
ベルヌーイ数の応用範囲は広大である。べき乗和の計算や、様々な関数の級数展開において重要な役割を果たす。特に、リーマンゼータ関数との深い関連は、現代数学における未解決問題の一つであるリーマン予想との関係でも注目されている。また、三角関数や双曲線関数の展開式にも登場し、これらの関数の性質を理解する上で重要な鍵となっている。
計算面では、直接的なマクローリン展開による計算は実用的でないため、特別な漸化式が用いられる。しかし、これにも課題がある。大きな数の計算では、浮動小数点数による計算の精度が著しく低下するという問題が生じる。この問題に対しては、現代では多倍長演算や特殊なアルゴリズムを用いた計算方法が研究されている。
興味深いことに、ベルヌーイ数は現代のコンピュータサイエンスにおいても重要な役割を果たしている。例えば、数値計算アルゴリズムの効率化や、暗号理論における素数の性質の研究などにも応用されている。
このように、ベルヌーイ数は純粋数学の美しさと、実用的な応用の両面で重要な意味を持つ数列である。その研究は現在も続いており、新たな数学的発見への道を開き続けている。
ここにも同じように書いておくと
リーマン・ゼータ関数の値を計算する重要な要素である

上記でn=1の場合を考えると、バーゼル問題の解決になる。
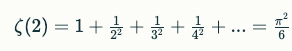
応用の例として、素数分布、公式の導出、解析的整数論での応用などに広く用いられる。数学の基本である。
プログラミング
先述のマクローリン展開などは、漸化式が使われるのだ。BASICでエイダが作ったプログラミングをしてみると以下のようになる。
// エイダ・ラブレス式ベルヌーイ数計算アルゴリズム
注釈:ベルヌーイ数の計算
操作カード No.1
変数 N を 1 に設定する
変数 R を 1 に設定する
操作カード No.2
N が 8 より大きい場合、操作カード No.25 へ移動
操作カード No.3
変数 D を N で割る
結果を変数 T に格納
操作カード No.4
T と R を掛け合わせる
結果を変数 R に格納
操作カード No.5
N に 1 を加える
操作カード No.2 へ戻る
[以下、操作カード No.25まで続く]エイダが書いたコードではない、
というのは、エイダ自身が考案したのは、抽象的なアルゴリズムであるからだ。複雑な計算手順をループ構造として表現し、加減乗除のみの基本演算で複雑な計算ロジックを実現した。
サブルーチンという考え方を導入したのもエイダだと言われているが、それはどんなものか、彼女の書いた本などを参照しないとわからないことが多い。噂では、バベッジと共同作業であり、数学的表現自体はバベッジがだいぶ力を貸したらしい。
でもエイダの新規性は数学の世界にとどまらないのである。
彼女は記号にできるものはなんでもコンピュータが解決できると言い放ったのである。今日はその通りに実現されている先駆的な考え方だ。
たしかに音は波であるので、信号として捉えることができる。
色だって光の3元素がどれくらい混じり合っているかの度合いRBGがわかれば画面に出力できるのと同様のことである。
でも私見では、このような考え方の大元にはライプニッツがいると思っている。
音楽とコンピュータ
コンピュータによる音楽生成の歴史は、エイダ・ラブレスの先見的な洞察から始まり、実に興味深い発展を遂げてきた。
初期の実験として、1950年のCSIR Mark 1による音楽生成は、現代の我々から見れば極めて素朴なものであった。しかし、この取り組みは、コンピュータが芸術的な創造性を持ち得るという可能性を示した画期的な出来事として評価できる。当時のプログラマーたちは、限られた計算能力の中で、いかに音楽的な要素を数値化し表現するかという根本的な課題に直面していたことだろう。
1950年代後半から1960年代にかけての基礎技術の確立期は、特に注目に値する。マックス・マシューズによるMUSIC-Iの開発は、現代のデジタル音楽制作の礎を築いた。特にGROOVEシステムは、リアルタイムの音楽制御という革新的なアプローチを示した点で、現代のDAWソフトウェアの原型と言えるだろう。
1970年代から1980年代のデジタル革命期は、技術の民主化という観点で重要な時期となった。ローランドMC-8やヤマハDX7の登場は、プロフェッショナルな音楽制作の現場に大きな変革をもたらした。私が学生時代に触れたPC-8800シリーズのFM音源は、当時としては画期的な音楽表現を可能にし、多くのプログラマーや音楽家たちの創造性を刺激した。MIDIの標準化は、異なるメーカーの機器間での互換性を確保し、音楽制作の可能性を大きく広げた点で、産業史上でも特筆すべき出来事といえる。
1990年代以降のAI時代への突入は、音楽生成の質的な転換点となった。EMIの開発は、人工知能が単なる音の生成を超えて、音楽的な文脈や様式を理解し、再現できることを示した。この時期の研究は、現在の深層学習による音楽生成の理論的基盤を形成したと言える。
2010年代以降の現代では、GANやTransformerモデルの登場により、音楽生成の技術は新たな段階に入った。これらのモデルを活用した音楽生成の実験を行っているが、特にTransformerモデルによる長期的な音楽構造の把握と生成は、まさにエイダ・ラブレスが予見した「創造的なコンピュータ」の実現に近づいていると感じている。技術の進歩は、芸術創造の本質とは何かという哲学的な問いも我々に投げかけている。
創造的なコンピュータと書いたが、コンピュータは再現できるのであり、創造するわけではない。
でも人間の創造を助ける道具に大いになる。
その発想はライプニッツが構想して、のちにエイダのような人物がそれを継承し、工学的な技術の進歩によって実現されている。実に生き生きとした歴史である。
あとがき
私はプログラミングが仕事なのであるが、効率的なプログラマーではないという自覚がある。アルゴリズムに興味があっても先駆的なライブラリに興味が薄い、タイアの発見をしてしまう癖があるとも言える。
それはともかくも、こうした工学についても これからは情報を取得していこうと思う。次回は、アロエヨーグルトについて話を戻してみようと思う。
