
【Python】ばね弾性力+重力による運動(単振動運動)
続いて、ばね弾性力による運動だよ。ばね弾性力とは平衡点からの変位に対して生じる復元力だね。ばね定数($${k}$$)に変位を掛けた量が線形ばね弾性力として定義されるね。重力も含めて物体に加わる力は次のとおりだよ。
$$
\boldsymbol{F} =m\boldsymbol{g} -k\boldsymbol{r}(t)
$$
力が与えられればニュートンの運動方程式( $${\boldsymbol{a} = \boldsymbol{F} / m }$$ )から、物体の加速度は次のように与えられるね。
$$
\boldsymbol{a} =\boldsymbol{g} - \frac{k}{m}\boldsymbol{r}(t)
$$
Pythonによる計算結果
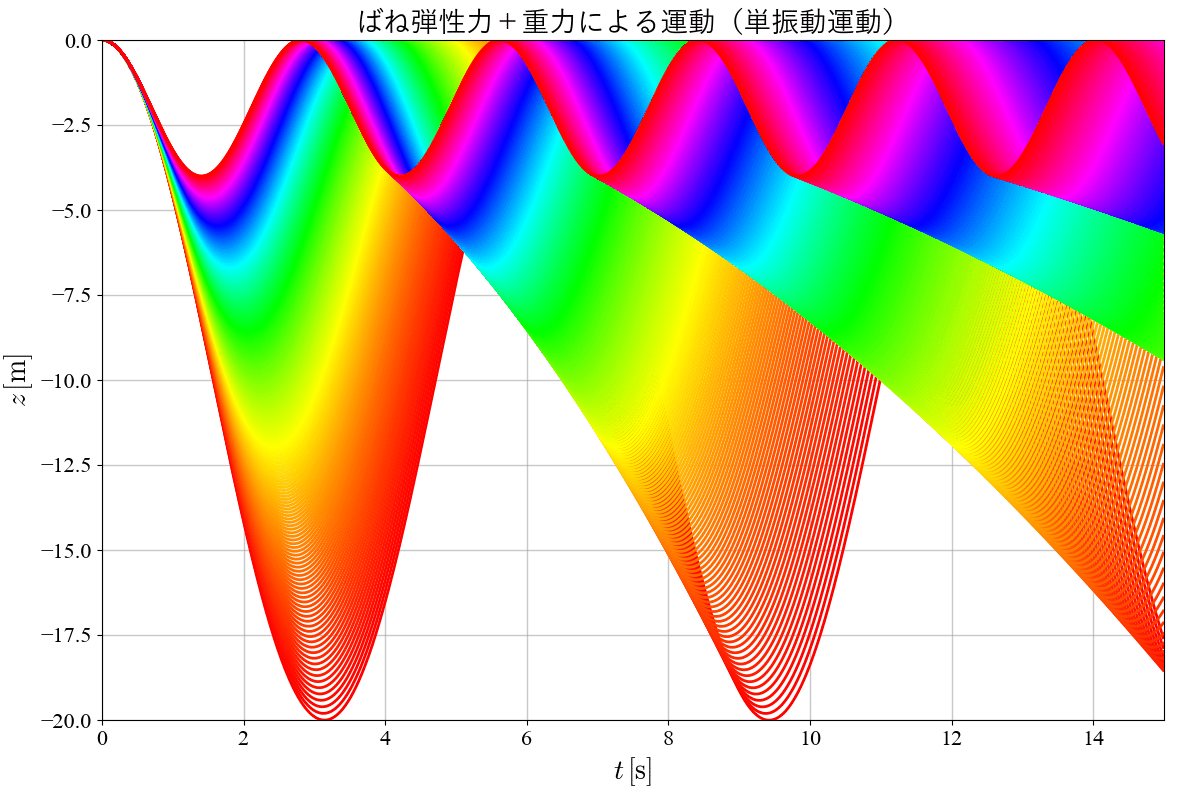
次のグラフは重力加速度$${\boldsymbol{g}=(0,0,-10)}$$、質量$${m=1}$$、初速度$${0}$$、初期位置を原点として、ばね定数を $${k=1.0\sim5.0}$$まで変化させたときの時間発展の様子だよ。運動の様子は単純な三角関数で表すことのできる単振動運動となるね。
プログラムソース(Python)
#################################################################
TITLE = "ばね弾性力+重力による運動(単振動運動)"
#################################################################
import numpy as np
import scipy.integrate as integrate
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import colorsys
###############################
# 実験室グローバル変数
###############################
TIME_START = 0.0 #計算開始時刻
TIME_END = 15.0 #計算終了時刻
DT = 0.01 #時間間隔
PLOT_FLAG = True #グラフ描画
ANIMATION_FLAG = False #アニメーション作成
ANIMATION_INTERVAL = 10 #アニメーション作成時の描画インターバル
###############################
# 計算グローバル変数
###############################
#時刻
times = np.arange(TIME_START, TIME_END, DT)
#重力加速度
vec_g = np.array([0, 0, -10])
#質量
m = 1.0
#ばね定数
ks = np.arange(1.0, 5.01, 0.01)
#ks = np.arange(5.0, 10.01, 0.1)
#粘性係数
gamma = 0.0
#初期位置
vec_r0 = np.array([0, 0, 0])
#初期速度
vec_v0 = np.array([0, 0, 0])
###############################
# 関数定義
###############################
#ばね弾性力+重力の微分方程式
def equations(t, X , vec_g, m, gamma, k):
vec_r = np.array([ X[0], X[1], X[2] ])
vec_v = np.array([ X[3], X[4], X[5] ])
vec_a = vec_g - k * vec_r - gamma / m * vec_v
return [vec_v[0], vec_v[1], vec_v[2], vec_a[0], vec_a[1], vec_a[2]]
# k 依存性を可視化
def calculation( k ):
solution = integrate.solve_ivp(
equations, #常微分方程式
method = 'RK45', #計算方法
args = (vec_g, m, gamma, k), #引数
t_span=( times[0], times[-1]), #積分区間
y0 = np.concatenate([vec_r0, vec_v0]), #初期値
t_eval = times #結果を取得する時刻
)
#計算結果
return solution.y[ 0 ], solution.y[ 1 ], solution.y[ 2 ]
##########################################################
if __name__ == "__main__":
#描画用リスト
xls = []
yls = []
#k による違い
for k in ks:
x, y, z = calculation( k )
xls.append( x )
yls.append( z )
if( PLOT_FLAG ):
#################################################################
# グラフの設定
#################################################################
fig = plt.figure( figsize=(12, 8) ) #画像サイズ
plt.subplots_adjust(left = 0.085, right = 0.97, bottom = 0.10, top = 0.95) #グラフサイズ
plt.rcParams['font.family'] = 'Times New Roman' #フォント
plt.rcParams['font.size'] = 16 #フォントサイズ
plt.rcParams["mathtext.fontset"] = 'cm' #数式用フォント
#カラーリストの取得
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
#グラフタイトルと軸ラベルの設定
plt.title( TITLE, fontname="Yu Gothic", fontsize=20, fontweight=500 )
plt.xlabel( r"$t \,[{\rm s}]$", fontname="Yu Gothic", fontsize=20, fontweight=500 )
plt.ylabel( r"$z \,[{\rm m}]$" , fontname="Yu Gothic", fontsize=20, fontweight=500 )
#罫線の描画
plt.grid( which = "major", axis = "x", alpha = 0.7, linewidth = 1 )
plt.grid( which = "major", axis = "y", alpha = 0.7, linewidth = 1 )
#描画範囲を設定
plt.xlim([0, TIME_END])
plt.ylim([-20.0, 0])
#グラフの描画
for i in range(len(ks)):
c = colorsys.hls_to_rgb( i/len(ks) , 0.5 , 1)
plt.plot(times, yls[i], linestyle='solid', linewidth = 2, color = c)
#グラフの表示
plt.show()
if( ANIMATION_FLAG ):
#################################################################
# アニメーションの設定
#################################################################
fig = plt.figure( figsize=(12, 8) ) #画像サイズ
plt.subplots_adjust(left = 0.085, right = 0.97, bottom = 0.10, top = 0.95) #グラフサイズ
plt.rcParams['font.family'] = 'Times New Roman' #フォント
plt.rcParams['font.size'] = 16 #フォントサイズ
plt.rcParams["mathtext.fontset"] = 'cm' #数式用フォント
#カラーリストの取得
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
#アニメーション作成用
imgs = []
#アニメーション分割数
AN = len( times )
#軌跡リスト
r_trajectorys = [ 0.0 ] * len( ks )
#アニメーションの各グラフを生成
for an in range( AN ):
t = DT * an
if( an % ANIMATION_INTERVAL != 0): continue
for i in range( len( ks ) ):
c = colorsys.hls_to_rgb( i/len(ks) , 0.5 , 1)
k = ks[ i ]
if( i == 0 ):
img = plt.plot([k], [yls[i][an]], color = c, marker = 'o', markersize = 15)
else:
img += plt.plot([k], [yls[i][an]], color = c, marker = 'o', markersize = 15)
img += plt.plot([ k, k ], [0, yls[i][an]], color = c, linestyle='solid', linewidth = 2 )
#時刻をグラフに追加
time = plt.text(13.5, 0.35, "t = " + str("{:.2f}".format(t)), fontsize=18)
img.append( time )
imgs.append( img )
#グラフタイトルと軸ラベルの設定
plt.title( TITLE, fontname="Yu Gothic", fontsize=20, fontweight=500 )
plt.xlabel( r"$k \,[{\rm N/m}]$", fontname="Yu Gothic", fontsize=20, fontweight=500 )
plt.ylabel( r"$z \,[{\rm m}]$" , fontname="Yu Gothic", fontsize=20, fontweight=500 )
#罫線の描画
plt.grid( which = "major", axis = "x", alpha = 0.7, linewidth = 1 )
plt.grid( which = "major", axis = "y", alpha = 0.7, linewidth = 1 )
#描画範囲を設定
plt.xlim([5, 10])
plt.ylim([-4.2, 0])
#アニメーションの生成
ani = animation.ArtistAnimation(fig, imgs, interval=50)
#アニメーションの保存
#ani.save("output.html", writer=animation.HTMLWriter())
#ani.save("output.gif", writer="imagemagick")
#ani.save("output.mp4", writer="ffmpeg", dpi=360)
#グラフの表示
plt.show()
