
【粒子法 MPS法】アルゴリズムの改善:ECS法 ポアソン方程式の生成項の誤差補償
上記のnoteで解説したHS法に加えて、下記の書籍で詳しく解説してある標準MPSの高精度化に着手しているよ。目次は次のとおりだよ。
書籍:粒子法:連続体・混相流・粒状体のための計算科学
P.83 HS法 ポアソン方程式生成項の高精度化
P.85 HL法 ラプラシアンモデルの高精度化
P.87 ECS法 ポアソン方程式生成項の誤差補償
P.92 GC法 勾配モデルの高精度化
P109 DS法 人工斥力導入による安定化
P118 SPP法 表面粒子の境界条件適正化
P124 WPP法 壁面における境界条件適正化
高精度化第2弾はECS法(ポアソン方程式生成項の誤差補償)だよ。
書籍の順番ではラプラシアンモデルの高精度化を行うHL法を導入すべきなのだろうけど、書籍における導出過程に理解できないところ(勾配モデルにMPS法ではなく関係のないSPH法を用いる点)があることと、後で導入するGC法との関係性が不明確なこともあって(HL法はGC法の下位互換?)、単に自分が理解できていないだけなのだけれども、一旦見送りするね。今回は、ポアソン方程式の生成項(右辺)の誤差補償を目指すECS法の導入を行うよ。ECS法はHS法の上位互換の位置づけとなるよ。ではさっそく始めるね。
非圧縮流体の数値解析法であるMPS法の肝は、「圧力」そのものを、圧力を無視して仮計算した粒子の位置・速度($${\boldsymbol{r}^{(*)}, \boldsymbol{v}^{(*)} }$$)から、次の真の時刻において流体密度が一定となるために必要な「力」として計算している点だね。つまり、無理やり流体密度一定を満たすように圧力をかけるので、時間・空間において局所的な高圧(数倍程度)が発生してしまうんだよね。標準MPS法では、そのような圧力が満たすポアソン方程式の右辺に現れる速度の勾配を
$$
\left\langle\nabla\cdot\boldsymbol{v}\right\rangle^{(*)}_i = -\frac{1}{\rho^{(0)} }\,\frac{ D\rho_i^{(*)} }{D t} \simeq -\frac{1}{\Delta t}\, \frac{\rho_i^{(*)}-\rho^{(0)}}{\rho^{(0)}} \simeq -\frac{1}{\Delta t}\,\frac{n_i^{(*)}-n^{(0)}}{ n^{(0)}}
$$
と表したね。この量を改めて見てみると、この量は本来あるべき数密度$${ n^{(0)} }$$からのズレに比例した量となっているね。標準MPS法ではズレを時間間隔$${\Delta t}$$で割っているので、スパイク的な値が発生する主要因だったわけだね。一方、HS法では仮密度の時間微分を重み関数の時間微分として厳密に扱って、
$$
\frac{1}{\rho^{(0)} }\,\frac{ D\rho_i^{(*)} }{D t} \simeq\frac{1}{n^{(0)} }\,\frac{ Dn_i^{(*)} }{D t} =- \frac{1}{n^{(0)}} \sum\limits_{j\ne i} \frac{r_e}{|\boldsymbol{r}_j^{(*)}-\boldsymbol{r}^{(*)}_i|^3}\, (\boldsymbol{r}_j^{(*)}-\boldsymbol{r}^{(*)}_i) \cdot (\boldsymbol{v}_j^{(*)}-\boldsymbol{v}^{(*)}_i)
$$
のように計算したのだったね。この量を用いるとスパイク状の圧力は抑制することができたのだったね。今回紹介するECS法は誤差補償として本来あるべき値へ戻していくことを目的とした項を追加する計算アルゴリズムだよ。
追加する誤差補正の項は2つあるよ。1つ目は先にも挙げた本来の密度$${ n^{(0)} }$$に近づける項
$$
-\frac{\gamma}{\Delta t}\,\frac{n_i^{(k)}-n^{(0)}}{ n^{(0)}}
$$
2つ目はそもそも存在しないはずの密度変化を緩やかにする密度移動粘性項
$$
-\frac{\beta}{\Delta t}\,\frac{n_i^{(k)}-n_i^{(k-1)}}{ n^{(0)}}
$$
だよ。この2つの項を速度の発散項に加えて、
$$
\left\langle\nabla\cdot\boldsymbol{v}\right\rangle^{(*)}_i =-\frac{1}{n^{(0)} }\,\frac{ Dn_i^{(*)} }{D t} -\frac{\gamma}{\Delta t}\,\frac{n_i^{(k)}-n^{(0)}}{ n^{(0)}}-\frac{\beta}{n^{(0)} }\,\frac{ Dn_i^{(k)} }{D t}
$$
と与えるのがECS法だよ。第1項目はHL法のままだよ。2つのパラメータ($${\gamma}$$と$${\beta}$$)は小さな値($${10^{-3}}$$程度)をシミュレーション対象となるモデルに合わせて設定する必要があるのだけれども、この2つのパラメータをそれぞれ、
$$
\gamma = \frac{\Delta t}{ n^{(0)}}\left |\frac{ Dn_i^{(k)} }{D t} \right|\ , \ \beta = \left|\frac{n_i^{(k)}-n^{(0)}}{ n^{(0)}} \right|
$$
という形に動的に与える方法も提案されているよ。$${\gamma }$$は密度の時間変化が大きいほど、$${\gamma }$$ は本来の密度からのズレが大きいほど、それぞれ大きな値を取るように設定することで、それぞれの補正力を高めているわけだね。HS法で、仮数密度の時間微分は
$$
\frac{1}{n^{(0)} }\,\frac{ Dn_i^{(*)} }{D t} =- \frac{1}{n^{(0)}} \sum\limits_{j\ne i} \frac{r_e}{|\boldsymbol{r}_j^{(*)}-\boldsymbol{r}^{(*)}_i|^3}\, (\boldsymbol{r}_j^{(*)}-\boldsymbol{r}^{(*)}_i) \cdot (\boldsymbol{v}_j^{(*)}-\boldsymbol{v}^{(*)}_i)
$$
で計算したので、時刻$${k}$$の数密度の時間微分も同様に計算するよ。
$$
\frac{1}{n^{(0)} }\,\frac{ Dn_i^{(k)} }{D t} =- \frac{1}{n^{(0)}} \sum\limits_{j\ne i} \frac{r_e}{|\boldsymbol{r}_j^{(k)}-\boldsymbol{r}^{(k)}_i|^3}\, (\boldsymbol{r}_j^{(k)}-\boldsymbol{r}^{(k)}_i) \cdot (\boldsymbol{v}_j^{(k)}-\boldsymbol{v}^{(k)}_i)
$$
ECS法アルゴリズム導入結果
下図のように高さ0.1メートル水を自由落下させて底面に衝突させるシミュレーションを行うよ。比較対象として4つのパターンで計算するよ。

1:標準MPS法
2:標準MPS法 + HS法
3:標準MPS法 + HS法 + ECS法
4:標準MPS法 + HS法 + ECS法(体積保存係数に固定値を加えた)
下の図は4パターンそれぞれの20秒後の結果だよ。「標準MPS法」は自由落下後の底面との衝突後に大きくバウンドして一部は外に飛び出るよ。体積保存性は良いのだけれども、局所的・局時的な高圧が発生してしまう関係で時間とともに振動が大きくなってしまうね。「標準MPS法 + HS法」の圧力分布は安定的だけれども、体積保存性に難があるね。さらには水深が1メートルを超えると底面から漏れ出てしまっているね。「標準MPS法 + HS法 + ECS法」では、上記の通りのECS法を導入した結果なのだけれども、体積保存性は幾分改善されているけれども、底面から漏れ出てしまっているね。体積を保存させる力が弱すぎるのだと考えられるね。

そこで、体積を保存させる力を決めるパラメータを次のように固定値を加えて計算した結果が一番右の結果だよ。体積保存性は格段に改善されたね。この固定値がどの程度の値が良いのかは後日改めて検証するね。
$$
\gamma = \frac{\Delta t}{ n^{(0)}}\left |\frac{ Dn_i^{(k)} }{D t} \right| + 0.01
$$
【追記】2024/09/30 体積保存を決める係数に追加する固定値依存性
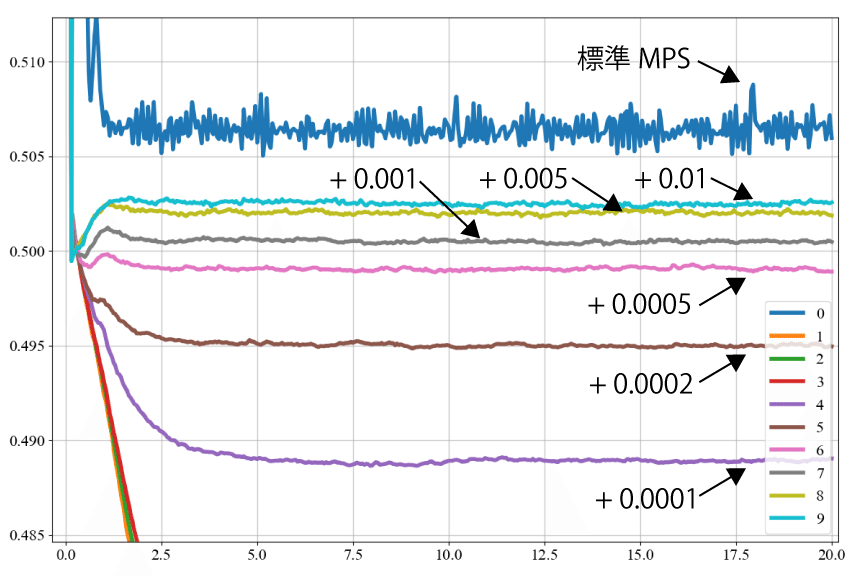
次の図は先に挙げた $${\gamma}$$ に追加する固定値の違いを比較するために、先のシミュレーションにて流体粒子のy座標(高さ方向)の平均値の時間依存性を計算した結果だよ(漏れ出た粒子は計算対象外)。先に示した20秒後のスナップショットでも示したとおり、「標準MPS法 + HS法」並びに「標準MPS法 + HS法 + ECS法」では底面から漏れ出てしまう結果から高さはどんどん低くなってしまっているね。$${\gamma}$$に追加する固定値を「0.00001」とした場合、途中で下げ止まっているので底面の水圧が低下した結果、体積を保存する力と底面での水圧が釣り合ったのだろうね。

次の図はグラフを拡大した結果だよ。$${\gamma}$$ に追加する固定値は大きくなるほど、高さが高くなっているね。長時間後に非圧縮静水状態になるとすると高さの平均値は「0.50」となることから、「0.50」を下回っている「+0.0001」「+0.0002」「+0.0005」では固定値が小さすぎるね。今回は自由落下後のさざ波で平均値は「0.50」を少し上回ることが考えられるから「+0.001」程度が良いのかもしれないね。今回の結果でわかったのは、底面の水圧が体積保存力を上回ると粒子が壁から漏れてしまうわけなので、$${\gamma}$$ に追加する固定値は水圧に比例した値にするのが妥当だろうね。今後の検証課題とするね。
Pythonプログラム
以下は標準MPS法にHS法を加えたPythonプログラムソースを販売するよ。もし良かったら試してみてください。
ここから先は
¥ 500
この記事が気に入ったらチップで応援してみませんか?
