
【Python】2重振子運動シミュレーション
上記で導出したアルゴリズムの適用例として、2重振子運動をシミュレーションしてみるね。
2重振子運動の計算アルゴリズム
2重振子運動の計算アルゴリズムの導出を行うね。強制振動運動させることを想定して支点の位置・速度・加速度ベクトルを$${\boldsymbol{r}_0, \boldsymbol{v}_0, \boldsymbol{a}_0}$$、2つの振り子の位置・速度と外力ベクトルをそれぞれ$${\boldsymbol{r}_1, \boldsymbol{v}_1, \boldsymbol{F}^{({\rm ex})}_1}$$と$${\boldsymbol{r}_2, \boldsymbol{v}_2, \boldsymbol{F}^{({\rm ex})}_2}$$と表します。2つの張力の大きさ$${f_{01}}$$と$${f_{12}}$$を導くね。
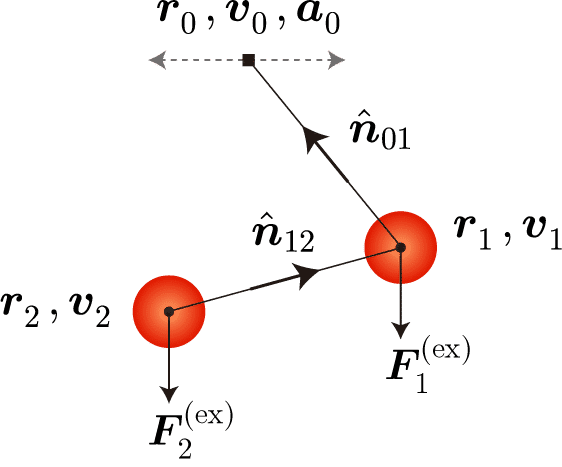
$${m_0=\infty}$$、方向ベクトルの$${\hat{\boldsymbol{n}}_{01}\cdot\hat{\boldsymbol{n}}_{12}}$$以外がすべて0であることを考慮して、$${(i,j)=(0,1), (i,j)=(1,2)}$$の組み合わせで得られる$${f_{01}}$$と$${f_{12}}$$に関する2つの方程式は次のとおりだね。
【運動方程式】張力($${f_{01}, f_{12}}$$ )に関する連立方程式
$$
-\frac{f_{01}}{m_1} + \frac{ \hat{\boldsymbol{n}}_{01}\cdot \hat{\boldsymbol{n}}_{12} }{m_1}\, f_{12} = A_{01}
$$
$$
\frac{ \hat{\boldsymbol{n}}_{01}\cdot \hat{\boldsymbol{n}}_{12}}{m_1}\, f_{01} -\left( \frac{1}{m_1} +\frac{1}{m_2} \right)f_{12} = A_{12}
$$
ただし、$${ A_{ij}}$$ は連立方程式の右辺
$$
A_{ij}= -\frac{1}{L_{ij}}\left[|\boldsymbol{v}_i-\boldsymbol{v}_j|^2+\left[ \frac{\boldsymbol{F}^{\,({\rm ex})}_i}{m_i} -\frac{\boldsymbol{F}^{\,({\rm ex})}_j}{m_j} \right] \cdot( \boldsymbol{r}_{i} - \boldsymbol{r}_{j} )\right]
$$
だよ。これを手で計算した結果、2重振子の2つのひもに加わる
2重振子の2つのひもの張力の大きさ
$$
f_{01}= -\left[ \frac{ m_1 (m_1+m_2) }{m_1+m_2[1-(\hat{\boldsymbol{n}}_{01}\cdot \hat{\boldsymbol{n}}_{12})^2]} \right] A_{01} - \left[ \frac{ m_1 m_2\,(\hat{\boldsymbol{n}}_{01}\cdot \hat{\boldsymbol{n}}_{12}) }{m_1+m_2[1-(\hat{\boldsymbol{n}}_{01}\cdot \hat{\boldsymbol{n}}_{12})^2]} \right]A_{12}
$$
$$
f_{12}= -\left[ \frac{ m_1 m_2\,(\hat{\boldsymbol{n}}_{01}\cdot \hat{\boldsymbol{n}}_{12}) }{m_1+m_2[1-(\hat{\boldsymbol{n}}_{01}\cdot \hat{\boldsymbol{n}}_{12})^2]} \right] A_{01} - \left[ \frac{ m_1m_2 }{m_1+m_2[1-(\hat{\boldsymbol{n}}_{01}\cdot \hat{\boldsymbol{n}}_{12})^2]} \right]A_{12}
$$
張力の大きさは$${f_{01}=f_{10}}$$、$${f_{12}=f_{21}}$$を満たす反面、方向ベクトルは$${\hat{\boldsymbol{n}}_{01}=-\hat{\boldsymbol{n}}_{10}}$$、$${\hat{\boldsymbol{n}}_{12}=-\hat{\boldsymbol{n}}_{21}}$$と符号が反転する点に注意しつつ各振り子に加わる全べての力ベクトルを計算することで、加速度ベクトルを得ることができるね。この加速度ベクトルは拘束条件を満たしているため、目的に応じた数値計算を行うことができるよ。
【計算アルゴリズム】2重振子の各振り子の加速度ベクトル(張力+重力)
$$
\boldsymbol{a}_{1} = \frac{\boldsymbol{F}_{1}}{m_1} = \frac{ \boldsymbol{f}_{01} + \boldsymbol{f}_{21}+ \boldsymbol{F}^{\,({\rm ex})}_1}{m_1} = \frac{f_{01}}{m_1}\, \hat{\boldsymbol{n}}_{01} - \frac{f_{12}}{m_1}\, \hat{\boldsymbol{n}}_{12} +\boldsymbol{g}
$$
$$
\boldsymbol{a}_{2} = \frac{\boldsymbol{F}_{2}}{m_2} = \frac{ \boldsymbol{f}_{12}+ \boldsymbol{F}^{\,({\rm ex})}_2}{m_2} = \frac{f_{12}}{m_2}\, \hat{\boldsymbol{n}}_{12} + \boldsymbol{g}
$$
【計算結果】張力+重力による2重振子のカオス運動
次のアニメーションは初期状態として2つのおもりを垂直に置いて、水平方向の初速度をわずかに変化させた2重振子の運動だよ。初期値の小さなズレがその後(わずか20秒程度)に決定的な違いが生じる運動のことはカオス運動と呼ばれるよ。2重振子運動もカウス運動が発生する系として有名だね。

今回の2重振子は張力に関する連立方程式を手で解きましたが、次回は任意の結合に対して連立方程式もPythonで計算できるように改良するよ。良かったら応援してください。
Pythonプログラムソース
Pythonプログラムソースを用意したよ。良かったら試してみてください。
#################################################################
TITLE = "任意の結合張力+重力による振り子運動1:2重振子"
#################################################################
import os
import numpy as np
import scipy.integrate as integrate
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import colorsys
###############################
# 実験室グローバル変数
###############################
TIME_START = 0.0 #計算開始時刻
TIME_END = 20.0 #計算終了時刻
DT = 0.01 #時間間隔
PLOT_FLAG = True #グラフ描画
ANIMATION_FLAG = True #アニメーション作成
ANIMATION_INTERVAL = 10 #アニメーション作成時の描画インターバル
OUTPUT_FLAG = False
OUTPUT_PASS = "./data/"
if( OUTPUT_FLAG and os.path.isdir(OUTPUT_PASS) == False) : os.mkdir(OUTPUT_PASS)
###############################
# 計算グローバル変数
###############################
#時刻
times = np.arange(TIME_START, TIME_END, DT)
#重力加速度
vec_g = np.array([0, 0, -10])
#質量
m1 = 1.0
m2 = 1.0
#粘性係数
gamma = 0.0
#ひもの長さ
L01_0 = 1.0
L12_0 = 1.0
#初速度の違い
v0s = np.arange(0.01, 0.0101, 0.000001)
#支点の振幅と角振動数
l = 0.0
omega_box = 0 * np.pi
###############################
# 関数定義
###############################
#支点の位置と速度
def box(t):
vec_r_box = np.array([ l * np.sin( omega_box * t ) , 0, 0])
vec_v_box = np.array([ l * omega_box * np.cos( omega_box * t ), 0, 0])
vec_a_box = np.array([ -l * omega_box**2 * np.sin( omega_box * t ), 0, 0])
return vec_r_box, vec_v_box, vec_a_box
#張力+重力の微分方程式
def equations(t, X):
vec_r1 = np.array([ X[0], X[1], X[2] ])
vec_v1 = np.array([ X[3], X[4], X[5] ])
vec_r2 = np.array([ X[6], X[7], X[8] ])
vec_v2 = np.array([ X[9], X[10], X[11] ])
#支点の位置ベクトル・速度ベクトル・加速度ベクトル
vec_r0, vec_v0, vec_a0 = box( t )
#相対ベクトル
vec_r01 = vec_r0 - vec_r1
vec_r12 = vec_r1 - vec_r2
#ひもの長さ
L01 = np.sqrt( np.dot(vec_r01, vec_r01) )
L12 = np.sqrt( np.dot(vec_r12, vec_r12) )
#相対単位ベクトル
vec_n01 = vec_r01 / L01
vec_n12 = vec_r12 / L12
#相対速度ベクトル
vec_v01 = vec_v0 - vec_v1
vec_v12 = vec_v1 - vec_v2
#相対速度の大きさ
v01 = np.sqrt( np.dot(vec_v01, vec_v01) )
v12 = np.sqrt( np.dot(vec_v12, vec_v12) )
#外力による加速度ベクトル
vec_a1 = vec_g
vec_a2 = vec_g
#相対加速度ベクトル
vec_a01 = vec_a0 - vec_a1
vec_a12 = vec_a1 - vec_a2
#A係数
A01 = -1.0 / L01 * ( v01**2 + np.dot(vec_a01, vec_r01) )
A12 = -1.0 / L12 * ( v12**2 + np.dot(vec_a12, vec_r12) )
#張力係数
f01 = - ( m1 * (m1 + m2) / ( m1 + m2 * ( 1.0 - np.dot( vec_n01, vec_n12)**2 ) ) ) * A01 - ( m1 * m2 * np.dot( vec_n01, vec_n12)/ ( m1 + m2 * ( 1.0 - np.dot( vec_n01, vec_n12)**2 ) ) ) * A12
f12 = - ( m1 * m2 * np.dot( vec_n01, vec_n12) / ( m1 + m2 * ( 1.0 - np.dot( vec_n01, vec_n12)**2 ) ) ) * A01 - ( m1 * m2 / ( m1 + m2 * ( 1.0 - np.dot( vec_n01, vec_n12)**2 ) ) ) * A12
#質点に加わる力
vec_F1 = f01 * vec_n01 - f12 * vec_n12 + m1 * vec_g
vec_F2 = f12 * vec_n12 + m2 * vec_g
#ニュートンの運動方程式
vec_a1 = vec_F1 / m1
vec_a2 = vec_F2 / m2
return [
vec_v1[0], vec_v1[1], vec_v1[2], vec_a1[0], vec_a1[1], vec_a1[2],
vec_v2[0], vec_v2[1], vec_v2[2], vec_a2[0], vec_a2[1], vec_a2[2]
]
# theta 依存性を可視化
def calculation(vec_r1, vec_v1, vec_r2, vec_v2 ):
solution = integrate.solve_ivp(
equations, #常微分方程式
method = 'RK45', #計算方法
args = (), #引数
t_span=( times[0], times[-1]), #積分区間
rtol = 1.e-10, #相対誤差
atol = 1.e-10, #絶対誤差
y0 = np.concatenate([vec_r1, vec_v1, vec_r2, vec_v2]), #初期値
t_eval = times #結果を取得する時刻
)
#計算結果
vec_r1_t = np.array( [solution.y[0], solution.y[1], solution.y[2]] )
vec_v1_t = np.array( [solution.y[3], solution.y[4], solution.y[5]] )
vec_r2_t = np.array( [solution.y[6], solution.y[7], solution.y[8]] )
vec_v2_t = np.array( [solution.y[9], solution.y[10], solution.y[11]] )
return vec_r1_t, vec_v1_t, vec_r2_t, vec_v2_t
##########################################################
if __name__ == "__main__":
#描画用リスト
x1ls = []
y1ls = []
z1ls = []
v1xls = []
v1yls = []
v1zls = []
x2ls = []
y2ls = []
z2ls = []
v2xls = []
v2yls = []
v2zls = []
lls = []
for i in range( len(v0s) ):
print( i )
v0 = v0s[ i ]
#初期位置と速度
vec_r1 = np.array([ 0, 0, L01_0])
vec_v1 = np.array([ 0, 0, 0])
vec_r2 = np.array([ 0, 0, L01_0+L12_0])
vec_v2 = np.array([ v0, 0, 0])
vec_r1_t, vec_v1_t, vec_r2_t, vec_v2_t = calculation( vec_r1, vec_v1, vec_r2, vec_v2 )
x1ls.append( vec_r1_t[0] )
y1ls.append( vec_r1_t[1] )
z1ls.append( vec_r1_t[2] )
v1xls.append( vec_v1_t[0] )
v1yls.append( vec_v1_t[1] )
v1zls.append( vec_v1_t[2] )
x2ls.append( vec_r2_t[0] )
y2ls.append( vec_r2_t[1] )
z2ls.append( vec_r2_t[2] )
v2xls.append( vec_v2_t[0] )
v2yls.append( vec_v2_t[1] )
v2zls.append( vec_v2_t[2] )
if( OUTPUT_FLAG ):
for i in range(len(times)):
t = i * DT
vec_r_box, vec_v_box, vec_a_box = box( t )
path = OUTPUT_PASS + str( i ) + '.txt'
f = open(path, 'w')
for j in range( len(x1ls) ):
#L01 = np.sqrt( (x1ls[ j ][ i ] - vec_r_box[ 0 ])**2 + (y1ls[ j ][ i ] - vec_r_box[ 1 ])**2 + (z1ls[ j ][ i ] - vec_r_box[ 2 ])**2 )
#L12 = np.sqrt( (x2ls[ j ][ i ] - x1ls[ j ][ i ])**2 + (y2ls[ j ][ i ] - y1ls[ j ][ i ])**2 + (z2ls[ j ][ i ] - z1ls[ j ][ i ])**2 )
#print( L01, L12 )
f.write(
str(round( x1ls[ j ][ i ], 2)) + "\t" + str(round( y1ls[ j ][ i ], 2)) + "\t" + str(round( z1ls[ j ][ i ], 2)) + "\t" + str(round( v1xls[ j ][ i ], 2)) + "\t" + str(round( v1yls[ j ][ i ], 2)) + "\t" + str(round( v1zls[ j ][ i ], 2)) + "\t" +
str(round( x2ls[ j ][ i ], 2)) + "\t" + str(round( y2ls[ j ][ i ], 2)) + "\t" + str(round( z2ls[ j ][ i ], 2)) + "\t" + str(round( v2xls[ j ][ i ], 2)) + "\t" + str(round( v2yls[ j ][ i ], 2)) + "\t" + str(round( v2zls[ j ][ i ], 2)) + "\n"
)
f.close()
if( PLOT_FLAG ):
#################################################################
# グラフの設定
#################################################################
fig = plt.figure( figsize=(12, 8) ) #画像サイズ
plt.subplots_adjust(left = 0.085, right = 0.97, bottom = 0.10, top = 0.95) #グラフサイズ
plt.rcParams['font.family'] = 'Times New Roman' #フォント
plt.rcParams['font.size'] = 16 #フォントサイズ
plt.rcParams["mathtext.fontset"] = 'cm' #数式用フォント
#カラーリストの取得
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
#グラフタイトルと軸ラベルの設定
plt.title( TITLE, fontname="Yu Gothic", fontsize=20, fontweight=500 )
plt.xlabel( r"$t \,[{\rm s}]$", fontname="Yu Gothic", fontsize=20, fontweight=500 )
plt.ylabel( r"$z \,[{\rm m}]$" , fontname="Yu Gothic", fontsize=20, fontweight=500 )
#罫線の描画
plt.grid( which = "major", axis = "x", alpha = 0.7, linewidth = 1 )
plt.grid( which = "major", axis = "y", alpha = 0.7, linewidth = 1 )
#描画範囲を設定
plt.xlim([0, TIME_END])
plt.ylim([-2.0, 2.0])
#グラフの描画
for i in range(len(v0s)):
c = colorsys.hls_to_rgb( i/len(v0s) , 0.5 , 1)
plt.plot(times, z1ls[i], linestyle='solid', linewidth = 2)
plt.plot(times, z2ls[i], linestyle='solid', linewidth = 2)
#グラフの表示
plt.show()
if( ANIMATION_FLAG ):
#################################################################
# アニメーションの設定
#################################################################
fig = plt.figure( figsize=(8.5, 6.5) ) #画像サイズ
plt.subplots_adjust(left = 0.095, right = 0.97, bottom = 0.10, top = 0.92) #グラフサイズ
plt.rcParams['font.family'] = 'Times New Roman' #フォント
plt.rcParams['font.size'] = 16 #フォントサイズ
plt.rcParams["mathtext.fontset"] = 'cm' #数式用フォント
#カラーリストの取得
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
#アニメーション作成用
imgs = []
#アニメーション分割数
AN = len( times )
#アニメーションの各グラフを生成
for an in range( AN ):
t = DT * an
vec_r_box, vec_v_box, vec_a_box = box( t )
if( an % ANIMATION_INTERVAL != 0): continue
for i in range( len( v0s ) ):
c = colorsys.hls_to_rgb( i/len(v0s) , 0.5 , 1)
if( i == 0 ):
img = plt.plot([ vec_r_box[0]], [vec_r_box[2]], marker = 'o', markersize = 15, color = c)
else:
img += plt.plot([ vec_r_box[0]], [vec_r_box[2]], marker = 'o', markersize = 15, color = c)
img += plt.plot([ x1ls[i][an]], [z1ls[i][an]], marker = 'o', markersize = 15, color = c)
img += plt.plot([ x2ls[i][an]], [z2ls[i][an]], marker = 'o', markersize = 15, color = c)
img += plt.plot([ vec_r_box[0], x1ls[i][an] ], [vec_r_box[2], z1ls[i][an]], linestyle='solid', linewidth = 2, color = c)
img += plt.plot([ x1ls[i][an], x2ls[i][an] ], [z1ls[i][an], z2ls[i][an]], linestyle='solid', linewidth = 2, color = c )
#時刻をグラフに追加
time = plt.text(13.5, 0.35, "t = " + str("{:.2f}".format(t)), fontsize=18)
img.append( time )
imgs.append( img )
#グラフタイトルと軸ラベルの設定
plt.title( TITLE, fontname="Yu Gothic", fontsize=20, fontweight=500 )
plt.xlabel( r"$x \,[{\rm m}]$", fontname="Yu Gothic", fontsize=20, fontweight=500 )
plt.ylabel( r"$z \,[{\rm m}]$" , fontname="Yu Gothic", fontsize=20, fontweight=500 )
#罫線の描画
plt.grid( which = "major", axis = "x", alpha = 0.7, linewidth = 1 )
plt.grid( which = "major", axis = "y", alpha = 0.7, linewidth = 1 )
#描画範囲を設定
plt.xlim([-2, 2])
plt.ylim([-2.0, 2.0])
#アニメーションの生成
ani = animation.ArtistAnimation(fig, imgs, interval=50)
#アニメーションの保存
#ani.save("output.html", writer=animation.HTMLWriter())
#ani.save("output.gif", writer="imagemagick")
ani.save("output.mp4", writer="ffmpeg", dpi=360)
#グラフの表示
#plt.show()
