
斜面を滑らずに転がる剛体球運動の計算アルゴリズム
剛体球が斜面を滑らずに転がる場合の計算アルゴリズムの導出を行うよ。下図は斜面を転がる剛体球の概念図だよ。斜面と剛体球の接点に働く摩擦力で回転運動が引き起こされると同時に、重心運動にも摩擦力の項が加えられるよ。
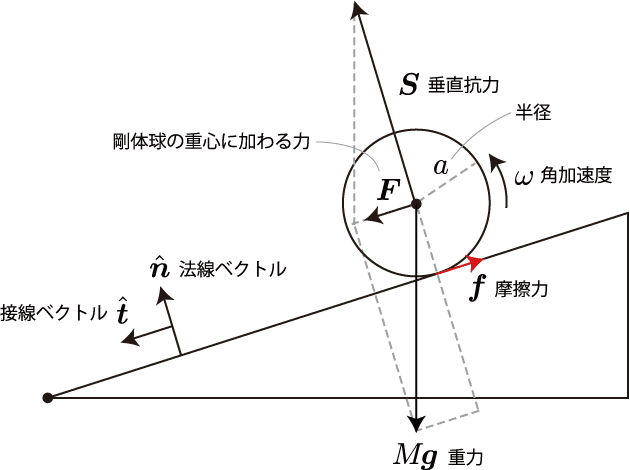
一般的に剛体が満たす運動方程式は並進運動と回転運動に関する方程式で表されるね。質量$${M}$$、慣性モーメント$${I}$$の剛体(位置ベクトル$${\boldsymbol{R}}$$、姿勢ベクトル$${\boldsymbol{\theta}}$$)に外力$${\boldsymbol{F}}$$、偶力$${\boldsymbol{N}}$$が加わったとすると次のように表されるよ。
$$
M\,\frac{d^2{\boldsymbol{R}}}{dt^2} = \boldsymbol{F}
$$
$$
I\,\frac{d^2{\boldsymbol{\theta}}}{dt^2} = \boldsymbol{N}
$$
1つ目はいわゆるニュートンの運動方程式だね。2つ目は角運動量 $${\boldsymbol{L} = I \boldsymbol{\omega}}$$の時間変化が偶力であるという関係
$$
\frac{d\boldsymbol{L}}{dt} = \boldsymbol{N}
$$
から導かれるね。この坂を転がる剛体球の問題を剛体の運動方程式に当てはめると次式のように与えられるよ。
$$
M\,\frac{d^2\boldsymbol{R}}{dt^2} =M\boldsymbol{g}+\boldsymbol{D}+\boldsymbol{f}
$$
$$
I\,\frac{d^2\boldsymbol{\theta}}{dt^2} =-a\hat{\boldsymbol{n}}\times\boldsymbol{f}
$$
上記の内、垂直抗力$${\boldsymbol{S}}と摩擦力$${\boldsymbol{f}}が未知だね。この運動方程式に対して運動の拘束条件を課すことで計算アルゴリズムの導出を行うよ。
重心運動の拘束条件
剛体球が斜面上を転がる場合、重心位置ベクトルに課せられる条件は斜面との接点ベクトルを$${\boldsymbol{R}_0}$$と表した場合、重心運動に対する拘束条件は
$$
\boldsymbol{R} =\boldsymbol{R}_0+a\,\hat{\boldsymbol{n}}, \frac{d\boldsymbol{R}}{dt}\cdot \hat{\boldsymbol{n}} =0,
\boldsymbol{v} \cdot \hat{\boldsymbol{n}}= \frac{d\boldsymbol{R}}{dt}\cdot \hat{\boldsymbol{n}} =0
$$
と表されるね。
回転運動の制約条件
「滑らない」という状況は、球体の回転で移動した距離と球体と斜面との接点の軌跡(円弧)が一致することだね。剛体球の初期状態の重心位置ベクトルと角度ベクトルをそれぞれ$${\boldsymbol{R}=0}$$、$${\boldsymbol{\theta}=0}$$とすると「滑らない」条件は
$$
\boldsymbol{R} = a \boldsymbol{\theta}\times \hat{\boldsymbol{n}}
$$
と表されそうだね。しかしながら、上記式は回転方向(回転軸方向)に変化がない場合でしか成り立たないね(もし角度ベクトルの向きが変化した場合、少なくとも位置ベクトルの向きは表式を満さないね)。むしろ、任意の回転運動で成り立つ拘束条件は、時間で微分した重心の運動速度と回転速度が一致する
$$
\frac{d\boldsymbol{R}}{dt} = a\boldsymbol{\omega}\times \hat{\boldsymbol{n}} \ , \ \boldsymbol{\omega}=\frac{ d\boldsymbol{\theta}}{dt}
$$
となりるね。$${\boldsymbol{\theta}}$$は角速度ベクトルです。また、さらに両辺を時間で微分した
$$
\frac{d^2\boldsymbol{R}}{dt^2} = a\,\frac{d^2\boldsymbol{\theta}}{dt^2}\times \hat{\boldsymbol{n}}
$$
も回転運動に対する拘束条件となるね。
斜面を転がる剛体球の計算アルゴリズム
並進運動と回転運動に対する拘束条件を運動方程式に課すことで、未知の量である垂直抗力$${\boldsymbol{S}}$$と摩擦力$${\boldsymbol{f}}$$を決定することができるね。導出の詳細は省略するけれども
$$
\boldsymbol{S} = -M(\boldsymbol{g}\cdot \hat{\boldsymbol{n}})\hat{\boldsymbol{n}}
$$
$$
\boldsymbol{f}=\frac{M}{1+\frac{Ma^2}{I}} \left[(\boldsymbol{g}\cdot \hat{\boldsymbol{n}})\, \hat{\boldsymbol{n}}-\boldsymbol{g}\right]
$$
この結果を踏まえて、斜面を滑らずに転がる剛体球の計算アルゴリズムは次のとおりだよ。位置ベクトルと角度ベクトルそれぞれ2階の微分方程式となっているので、ルンゲ・クッタ法などで数値的に計算することができるね。
$$
\frac{d^2\boldsymbol{R}}{dt^2} = \frac{1}{1+\frac{I}{Ma^2}} \left[\boldsymbol{g} -(\boldsymbol{g}\cdot \hat{\boldsymbol{n}})\, \hat{\boldsymbol{n}}\right]
$$
$$
\frac{d^2\boldsymbol{\theta}}{dt^2} = -\frac{1}{a}\,\frac{d^2\boldsymbol{R}}{dt^2}\times \hat{\boldsymbol{n}}
$$
ちなみに剛体球の慣性モーメントは
$$
I = \frac{2}{5}\, Ma^2
$$
なので、斜面を滑らない並進運動の方程式から$${M}$$も$${a}$$も消えるため、並進運動は質量にも半径にも依存しないことがわかるね。
運動の初期条件
今回「滑らない」ことを拘束条件としているので、並進運動の初速度$${\boldsymbol{V}(0)}$$に合わせて回転運動の初角速度ベクトル$${\boldsymbol{\omega}(0)}$$は一意に与える必要があるね。
$$
\boldsymbol{\omega}(0) = \frac{1}{a}\, \hat{\boldsymbol{n}}\times \boldsymbol{V}(0)
$$
シミュレーション結果
次のアニメーションは斜面の傾きの向きからずらした方向へ初速度(角速度)を与えたときの計算結果だよ。表示している矢印は角速度ベクトル$${\boldsymbol{\omega}}$$を表しているよ。また、左上の数値は計算誤差の大きさを把握するために計算した力学的エネルギーの変化だよ。意図通りの運動結果が得られていそうだね。
ちなみに力学的エネルギーは
$$
E = \frac{1}{2}\, M \boldsymbol{V}^2 -M\boldsymbol{g}\cdot \boldsymbol{R} +\frac{1}{2}\,I \boldsymbol{\omega}^2
$$
で与えられるよ。
