
【Python】サイクロイド曲線経路に拘束された質点の運動シミュレーション
導出した経路に拘束された質点運動をシミュレーションするための計算アルゴリズムを用いた4つ目の例としてサイクロイド曲線経路を取り上げるよ。計算に必要な経路に関する各種ベクトル(経路ベクトル・接線ベクトル・曲率ベクトル)の導出から始めるよ。
サイクロイド曲線の経路の経路ベクトル・接線ベクトル・曲率ベクトル

サイクロイド曲線とは上図のような円を転がしたときの固定された円周上の点の軌跡だよ。半径$${r}$$の円を原点からの角度$${\theta}$$回転させたとき、円の中心座標は$${( r\theta, r )}$$となり、円周上の固定点の座標はこの円の中心座標から$${x}$$方向に$${-\sin\theta}$$、$${y}$$方向に$${-r\cos\theta}$$移動させたところにあるので、サイクロイド曲線を表す媒介変数表示は次のとおりになるね。
サイクロイド曲線の媒介変数表示
$$
\left\{\begin{matrix} x(\theta )=r(\theta-\sin\theta) & \cr y(\theta ) =r(1-\cos\theta)& \end{matrix}\right.
$$
ただし、図は$${\pi/2<\theta<\pi}$$の様子を表しているので、$${\sin\theta>0}$$、$${\cos\theta<0}$$であることに注意してください。
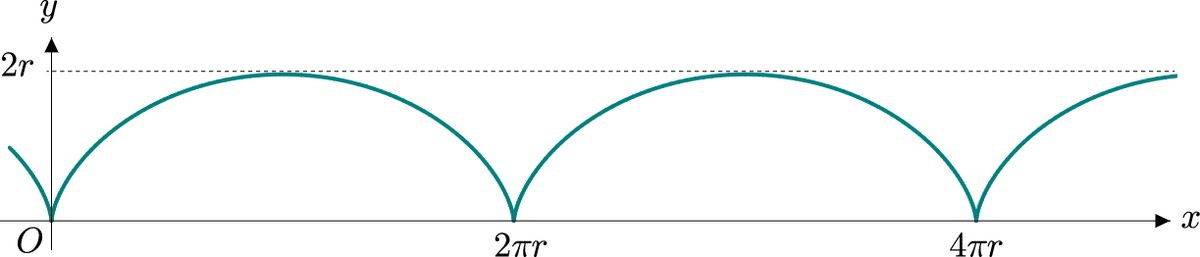
この式を用いてサイクロイド曲線を描画した結果が上だよ。$${\theta}$$は$${-\infty< \theta<\infty}$$で定義されるね。今回の経路は上記のサイクロイド曲線の上下を反転させた
$$
\left\{\begin{matrix} x(\theta )=r(\theta-\sin\theta) & \cr y(\theta ) =-r(1-\cos\theta)& \end{matrix}\right.
$$
とするね。これまでと同様、接線ベクトルと曲率ベクトルに必要な$${\theta}$$の$${l}$$微分を計算するよ。1回微分は
$$
\frac{d l}{d\theta } = \sqrt{2}r\sqrt{1-\cos\theta} \ \to \ \frac{d \theta}{dl } = \frac{1}{ \sqrt{2}r\sqrt{1-\cos\theta}}
$$
2回微分は
$$
\frac{d^2 \theta}{dl^2 } = \frac{d\theta}{dl}\,\frac{d }{d\theta}\left( \frac{1}{ \sqrt{2}r\sqrt{1-\cos\theta}}\right)=\frac{-\sin\theta}{4r^2\left(1-\cos\theta\right)^2}
$$
と与えられることから、サイクロイド曲線経路の接線ベクトルと曲率ベクトルは次のとおりに得られるね。
サイクロイド曲線経路の接線ベクトル
$$
\begin{array}{rrl}
\boldsymbol{t}_{\rm path} (\theta) & =& \frac{1}{\sqrt{2}\sqrt{1-\cos\theta}} \,(1-\cos\theta,\sin\theta) \\
&=& \frac{1}{\sqrt{2}}\,(\sqrt{1-\cos\theta}, \pm\sqrt{1+\cos\theta} )
\end{array}
$$
サイクロイド曲線経路の曲率ベクトル
$$
\boldsymbol{\chi} (\theta) = \frac{-1}{4r(1-\cos\theta)}\,(-\sin\theta,1-\cos\theta)
$$
となります。しかしながら、上記の接線ベクトルと曲率ベクトルは$${\theta=0}$$や$${\2pi}$$で分母が0になってしまい無限大に発散してしまうので、三角関数の関係式 $${\sin\theta = \pm \sqrt{1-\cos^2\theta} = \pm \sqrt{(1+\cos \theta )( 1 - \cos \theta )}}$$を考慮して変形するね。
サイクロイド曲線経路の接線ベクトル
$$
\boldsymbol{t}_{\rm path} (\theta)= \frac{1}{\sqrt{2}}\,(\sqrt{1-\cos\theta}, \pm\sqrt{1+\cos\theta} )
$$
サイクロイド曲線経路の曲率ベクトル
$$
\boldsymbol{\chi} (\theta) = \frac{-1}{4r}\, \left( \mp\sqrt{\frac{1+\cos\theta}{1-\cos\theta }},1\right)
$$
依然として曲率ベクトルの$${x}$$成分は$${\theta=0, 2\pi}$$で発散するのだけれども、これはサイクロイド曲線のもつ特異性で、この2点が特異点であることを意味しているよ。なお、接線ベクトルと曲率ベクトルの$${\pm}$$は$${\sin(theta)}$$の符号に対応するね。また、曲率ベクトルの大きさは
$$
\chi(\theta)=|\boldsymbol{\chi} (\theta)|= \frac{1}{2r\sqrt{2-2\cos\theta}}
$$
となることから$${\theta}$$に依存するね。$${\theta=\pi}$$のときに最小値$${1/2\sqrt{2} r}$$をとり、$${\theta=0}$$と$${2\pi}$$で無限大に発散するね
媒介変数の取得方法
運動する物体の位置から媒介変数$${\theta}$$を計算するには$${y}$$から
$$
\theta = \arccos\left(1+\frac{z}{r}\right)
$$
と得られるわけだけれども、arccos関数は$${-1}$$から$${1}$$の引数に対して$${\pi}$$から$${0}$$を返すので、$${\theta}$$を$${0}$$から$${2\pi}$$で取得するために$${x}$$の値で場合分けが必要となるね。また、数値計算では計算誤差のためにサイクロイド曲線を表すパラメータ$${r}$$の補正値を取得が必要となるわけだけれども、これはサイクロイド曲線の微分方程式を$${r}$$について解いた
$$
r = \frac{y}{2}\left[1+\left(\frac{dy}{dx}\right)^2 \right] = \frac{y}{2}\left[1+\left(\frac{v_y}{v_x}\right)^2 \right]
$$
で計算することができるね($${dy/dx = (dy/dt)/(dx/dt) = v_y/v_x}$$)。この式を用いることで、任意の時刻の物体の位置と速度から、物体が現在運動しているサイクロイド曲線の$${r}$$パラメータを計算することができるわけだね。さっそく計算結果を示すよ。
計算結果
Pythonプログラムソース
上記のシミュレーションを行うプログラムソースを公開するよ。もしよかったら試してみてください。これからも応援してください。よろしくお願いしまーす!
#################################################################
TITLE = "経路に拘束された運動(サイクロイド曲線)"
#################################################################
import os
import numpy as np
import scipy.integrate as integrate
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import colorsys
###############################
# 実験室グローバル変数
###############################
TIME_START = 0 #計算開始時刻
TIME_END = 4.12 #計算終了時刻
DT = 0.01 #時間間隔
PLOT_FLAG = True #グラフ描画
ANIMATION_FLAG = False #アニメーション作成
ANIMATION_INTERVAL = 5 #アニメーション作成時の描画インターバル
OUTPUT_FLAG = False
OUTPUT_PASS = "./data/"
if( OUTPUT_FLAG and os.path.isdir(OUTPUT_PASS) == False) : os.mkdir(OUTPUT_PASS)
###############################
# 計算グローバル変数
###############################
#時刻
times = np.arange(TIME_START, TIME_END, DT)
#重力加速度
vec_g = np.array([0, 0, -10])
#質量
m = 1.0
#初期位置
#thetas = [ 0.01 ]
thetas = np.arange(0.01, 0.70, 0.001)
#v0s = np.arange(10, 11.0+0.1, 0.02)
###############################
# 関数定義
###############################
#相対誤差
rtol = 1e-9
#絶対誤差
atol = 1e-9
#補正ばね弾性係数
compensationK = 0.004
#補正粘性抵抗係数
compensationGamma = 0.4
# 経路の設定
class Path:
#コンストラクタ
def __init__(self):
#始点と終点のx座標
self.x_start = -1.5
self.x_end = 1.5
#サイクロイド曲線パラメータr
self.R = (self.x_end - self.x_start) / (2.0 * np.pi)
#始点と終点のz座標
self.path_z0 = 2.0 * self.R; #最下点が0となるように
#サイクロイド曲線始点の位置ベクトル
self.path_start = np.array([self.x_start, 0, self.path_z0])
#経路の位置ベクトルを指定する媒介変数関数
def position( self, theta ):
x = self.R * (theta - np.sin(theta)) + self.path_start[0]
y = 0
z = -self.R * (1.0 - np.cos(theta)) + self.path_start[2]
return np.array([x, y, z])
#接線ベクトルを指定する媒介変数関数
def tangent( self, theta ):
A = 1.0 / np.sqrt(2.0)
x = A * np.sqrt(1.0 - np.cos( theta ))
y = 0
z = -A * np.sqrt(1.0 + np.cos( theta ))
if ( np.sin(theta) < 0 ): z = -z
return np.array([x, y, z])
#曲率ベクトルを指定する媒介変数関数
def curvature( self, theta ):
A = -1.0 / (4.0 * self.R)
x = -A * np.sqrt((1.0 + np.cos(theta)) / (1.0 - np.cos(theta)))
y = 0
z = -A
if (np.abs(x) == np.inf):
x = 0
z = 0
if (np.sin(theta) < 0): x = -x
return np.array([x, y, z])
#媒介変数の取得
def getTheta( self, r, v ):
#相対位置ベクトル
bar_r = r - self.path_start
if (np.abs(v[0]) > 1.0):
_R = np.abs(bar_r[2]) / 2.0 * (1.0 + (v[2] / v[0])**2 )
else:
_R = self.R
cos = 1.0 + bar_r[2] / _R
if( cos < -1 ): cos = -1
if( cos > 1 ): cos = 1
if (bar_r[0] < _R * np.pi):
theta = np.arccos(cos)
else:
theta = 2.0 * np.pi - np.arccos(cos)
return theta
#経路拘束力の微分方程式
def equations(t, X, path, compensationK, compensationGamma):
vec_r = np.array([ X[0], X[1], X[2] ])
vec_v = np.array([ X[3], X[4], X[5] ])
#媒介変数の取得
theta = path.getTheta ( vec_r, vec_v )
#媒介変数に対する位置ベクトル、接線ベクトル、曲率ベクトルの計算
position = path.position( theta )
tangent = path.tangent( theta )
curvature = path.curvature( theta )
#経路中心の位置ベクトル・速度ベクトル・加速度ベクトル
vec_r_box = np.copy( path.path_start )
vec_v_box = np.array([0.0, 0.0, 0.0])
vec_a_box = np.array([0.0, 0.0, 0.0])
#相対速度
bar_v = vec_v - vec_v_box
#微係数dl/dtとd^2l/dt^2を計算
dl_dt = np.dot( bar_v, tangent )
d2l_dt2 = np.dot( vec_g, tangent ) - np.dot( vec_a_box, tangent)
#加速度を計算
vec_a = vec_a_box + d2l_dt2 * tangent + dl_dt * dl_dt * curvature
#ズレ位置ベクトル
bar_r = vec_r - position
#補正ばね弾性力
fk = -compensationK * bar_r
#法線ベクトル
n1 = curvature / np.sqrt(np.sum( curvature**2 ))
n2 = np.cross(n1, tangent )
#補正粘性抵抗力
fgamma1 = -compensationGamma * np.dot( bar_v, n1 ) * n1
fgamma2 = -compensationGamma * np.dot( bar_v, n2 ) * n2
#経路補正力を加える
vec_a += (fk + fgamma1 + fgamma2)/m * np.abs(m*vec_a)
return [vec_v[0], vec_v[1], vec_v[2], vec_a[0], vec_a[1], vec_a[2]]
# 初速度依存性を可視化
def calculation(vec_r0, vec_v0, path, compensationK, compensationGamma):
solution = integrate.solve_ivp(
equations, #常微分方程式
method = 'RK45', #計算方法
args = (path, compensationK, compensationGamma), #引数
t_span=( times[0], times[-1]), #積分区間
rtol = rtol, #相対誤差
atol = atol, #絶対誤差
y0 = np.concatenate([vec_r0, vec_v0]), #初期値
t_eval = times #結果を取得する時刻
)
#計算結果
return solution.y[ 0 ], solution.y[ 1 ], solution.y[ 2 ], solution.y[ 3 ], solution.y[ 4 ], solution.y[ 5 ]
##########################################################
if __name__ == "__main__":
#経路の生成
path = Path()
#描画用リスト
xls = []
yls = []
zls = []
vxls = []
vyls = []
vzls = []
#初期位置による違い
for i in range(len(thetas)):
print( i )
theta = thetas[ i ] * np.pi
#初期位置と速度
vec_r0 = path.position( theta )
vec_v0 = np.array([ 0, 0, 0])
x, y, z, vx, vy, vz = calculation( vec_r0, vec_v0, path, compensationK, compensationGamma )
xls.append( x )
yls.append( y )
zls.append( z )
vxls.append( vx )
vyls.append( vy )
vzls.append( vz )
vec_r = np.array([ x[-1], y[-1], z[-1] ])
vec_v = np.array([ vx[-1],vy[-1],vz[-1] ])
E_start = 1.0/2.0 * m * np.sum( vec_v0**2 ) - m * np.dot( vec_g, vec_r0 )
E_end = 1.0/2.0 * m * np.sum( vec_v**2 ) - m * np.dot( vec_g, vec_r )
DeltaE = np.abs(E_end - E_start)
print( E_start, E_end, " |ΔE/E(0)| =", DeltaE / E_start )
if( OUTPUT_FLAG ):
for i in range(len(times)):
f_path = OUTPUT_PASS + str( i ) + '.txt'
f = open(f_path, 'w')
for j in range( len(xls) ):
f.write( str(round( xls[ j ][ i ], 4)) + "\t" + str(round( yls[ j ][ i ], 4)) + "\t" + str(round( zls[ j ][ i ], 4)) + "\t" + str(round( vxls[ j ][ i ], 4)) + "\t" + str(round( vyls[ j ][ i ], 4)) + "\t" + str(round( vzls[ j ][ i ], 4)) + "\n")
f.close()
if( PLOT_FLAG ):
#################################################################
# グラフの設定
#################################################################
fig = plt.figure( figsize=(12.8, 6.7) ) #画像サイズ
plt.subplots_adjust(left = 0.07, right = 0.98, bottom = 0.11, top = 0.95) #グラフサイズ
plt.rcParams['font.family'] = 'Times New Roman' #フォント
plt.rcParams['font.size'] = 16 #フォントサイズ
plt.rcParams["mathtext.fontset"] = 'cm' #数式用フォント
#カラーリストの取得
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
#グラフタイトルと軸ラベルの設定
plt.title( TITLE, fontname="Yu Gothic", fontsize=20, fontweight=500 )
plt.xlabel( r"$t \,[{\rm s}]$", fontname="Yu Gothic", fontsize=20, fontweight=500 )
plt.ylabel( r"$z \,[{\rm m}]$" , fontname="Yu Gothic", fontsize=20, fontweight=500 )
#罫線の描画
plt.grid( which = "major", axis = "x", alpha = 0.7, linewidth = 1 )
plt.grid( which = "major", axis = "y", alpha = 0.7, linewidth = 1 )
#描画範囲を設定
plt.xlim([0, TIME_END])
plt.ylim([0, 1])
#グラフの描画
for i in range(len(thetas)):
c = colorsys.hls_to_rgb( i/len(thetas) , 0.5 , 1)
plt.plot(times, zls[i], linestyle='solid', linewidth = 4, color = c)
#グラフの表示
plt.show()
if( ANIMATION_FLAG ):
#サイクロイド曲線配列の生成
path_thetas = np.linspace(0, 2*np.pi, 200)
cirsx = []
cirsy = []
for theta in path_thetas:
r = path.position( theta )
cirsx.append( r[ 0 ] )
cirsy.append( r[ 2 ] )
#################################################################
# アニメーションの設定
#################################################################
fig = plt.figure(figsize=(15, 5)) #画像サイズ
plt.subplots_adjust(left = 0.03, right = 0.99, bottom = 0.06, top = 0.92) #グラフサイズ
plt.rcParams['font.family'] = 'Times New Roman' #フォント
plt.rcParams['font.size'] = 16 #フォントサイズ
plt.rcParams["mathtext.fontset"] = 'cm' #数式用フォント
#カラーリストの取得
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
#アニメーション作成用
imgs = []
#アニメーション分割数
AN = len( times )
#軌跡リスト
r_trajectorys = [ 0.0 ] * len( thetas )
#アニメーションの各グラフを生成
for an in range( AN ):
t = DT * an
if( an % ANIMATION_INTERVAL != 0): continue
#軌跡の描画
img = plt.plot(cirsx, cirsy, color = "black", linestyle='dotted', linewidth = 1 )
for i in range( len( thetas ) ):
c = colorsys.hls_to_rgb( i/len(thetas) , 0.5 , 1)
if( i == 0 ):
img += plt.plot([xls[i][an]], [zls[i][an]], color = c, marker = 'o', markersize = 20)
else:
img += plt.plot([xls[i][an]], [zls[i][an]], color = c, marker = 'o', markersize = 20)
#時刻をグラフに追加
time = plt.text(13.5, 0.35, "t = " + str("{:.2f}".format(t)), fontsize=18)
img.append( time )
imgs.append( img )
#グラフタイトルと軸ラベルの設定
plt.title( TITLE, fontname="Yu Gothic", fontsize=20, fontweight=500 )
#plt.xlabel( r"$x \,[{\rm m}]$", fontname="Yu Gothic", fontsize=20, fontweight=500 )
#plt.ylabel( r"$z \,[{\rm m}]$" , fontname="Yu Gothic", fontsize=20, fontweight=500 )
#罫線の描画
plt.grid( which = "major", axis = "x", alpha = 0.7, linewidth = 1 )
plt.grid( which = "major", axis = "y", alpha = 0.7, linewidth = 1 )
#描画範囲を設定
plt.xlim([-1.6, 1.6])
plt.ylim([-0.1, 1.0])
#アニメーションの生成
ani = animation.ArtistAnimation(fig, imgs, interval=50)
#アニメーションの保存
#ani.save("output.html", writer=animation.HTMLWriter())
ani.save("output40.gif", writer="imagemagick")
ani.save("output40.mp4", writer="ffmpeg", dpi=360)
#グラフの表示
#plt.show()
