1. らくらくわかるボラティリティタックスのしくみ
(ポイント)
このノートではシミュレーションと実例を通じてボラティリティタックスとはなにかを紹介し、具体的な計算方法をわかりやすく説明します。また、ボラティリティタックスがあることで有利なギャンブルや投資でも必ずしも儲けられないことを示します。最後にボラティリティタックスを考慮した上での最適な投資比率(ギャンブルなら資金管理法)の見つけ方である「ケリーの公式」を紹介します。
1.1. ボラティリティの簡単な説明
まずはボラティリティとはなにかを感覚的に理解しましょう。ギャンブルをしない人にもなじみのある例として株式投資を例に考えます。
ある株に投資すると平均で1年に7%値上がりし、資産が増えるとしましょう。ただし定期預金のように確実に7%ずつ資産が増えるわけではありません。もっと多かったり、少なかったり、場合によっては減る可能性もあります。競馬に例えるなら100円の馬券を買ったら当たって120円返ってきたり、200円返ってきたり、外れて1円も返ってこなかったり(100円減る)といった感じです。何回も繰り返すと平均では賭けたお金が7%増えて返ってくるという状況です(※現実の競馬では平均で増えるようなうまい話はありませんので注意してください)。
株や競馬のように1日後、1年後または1レース後の収益がさまざまに変化することを「ボラティリティ(変動性)がある」と言います。また、株の種類によっては1年で3%上がったり下がったりするものもあれば、50%上がったり下がったりするものもあります。競馬で言えば勝つ可能性が高いけれどオッズが低い馬(本命)や勝つ可能性が低いけれどオッズが高い馬(大穴)がいます。収益が様々に動くといっても動き方に大小があるのです。変動率が大きくなりがちなときは「ボラティリティが高い」、小さい動く傾向のときは「ボラティリティが低い」と言います。
ただボラティリティが高いと低いだけでは少しぼんやりしているので昔の人々が変動性を数字で計算する方法を考えました。ばらつき度合いを把握することができれば何でもいいのですが、通常は「標準偏差」をボラティリティの物差しとして使います。観察する数字の単位に合わせて計算するのですがたいていの場合収益率はパーセントで計算するので、ボラティリティを測るときの標準偏差もパーセントで表現します。だいたいの仕組みとして、1日の標準偏差が1%といったとき、100日間株価の動きを観察するとそのうち68日(だいたい3分の2ですね)の値動きは平均の上下1%の範囲内に収まります。これが標準偏差1%のときのばらつき度合いと理解してください。「ボラティリティ」と「標準偏差」は厳密には違うのですがたいていの場合同じ意味で使って問題ありません。
マニア向けの本では標準偏差のことを$${\sigma}$$(シグマ)と書くことがよくあります。特に説明なく$${\sigma}$$と出てきたら標準偏差のことを指しているので覚えておいてください。また$${\sigma^2}$$(標準偏差の2乗)は「分散」と呼ばれ、これもデータの散らばり度合いを表す数字としてよく使われます。また、この種の数字で一番有名な「平均」はよく$${\mu}$$(ミュー)と書かれるので
$${\sigma}$$(シグマ):標準偏差
$${\sigma^2}$$(シグマ2乗):分散
$${\mu}$$(ミュー):平均
の3つの呼び方を覚えておきましょう。
(解説)標準偏差の計算
標準偏差はデータがたくさんあるとき、その特徴をシンプルに表現する数値(難しい言葉で「統計量」と言います)の一つです。データの散らばり度合いを表すことができるため、観察した全データの合計をデータの数で割った「平均」と並んで大切な統計量です。データが手に入れば株価の動きだけではなく、気温や人口、血圧、支持政党などあらゆるデータについて計算することができます。株価や為替など時系列に値が変化する金融関連データの標準偏差を特にボラティリティと呼ぶことが多いようです。
標準偏差の目的はデータがどれぐらいばらついているかを表すことなので、まずデータ全体の平均を計算します。続いて平均からどのくらいばらついているのか知るため、すべてのデータについて平均との差(難しい言葉で「偏差」と言います)を計算します。平均からのばらつきの大きさをみたいのですが、素直に偏差を合計すると差し引きゼロになってしまうので、全ての偏差を2乗してから合計します。合計した値をデータの数で割ると標準偏差が得られます。言い換えれば偏差の2乗の平均が標準偏差です。
平均と分散、標準偏差の計算式は次のとおりです。
$${i}$$番目のデータ:$${x_i}$$
$${n}$$個のデータの平均:$${\mu=\frac{x_1+x_2+\ldots+x_n}{n}}$$
$${n}$$個のデータの分散:$${\sigma^2=\frac{\left(x_1-\mu\right)^2+\left(x_2-\mu\right)^2+\ldots+\left(x_n-\mu\right)^2}{n}}$$
標準偏差:$${\sigma=\sqrt{\sigma^2}}$$
ただこの書き方だと面倒なので、マニアの間ではたくさん($${n}$$個)あるデータを全部合計するという意味の記号($${\sum_{i=1}^{n}x_i}$$)を使って平均、分散を表現することがよくあります。この記号を使って平均と分散の計算式を書くと次のようになります(標準偏差は上と同じなので省略します)。この式はいろいろな時に使うので覚えておきましょう
平均:$${\mu=\frac{1}{n}\sum_{i=1}^{n}x_i }$$ 式(1)
分散:$${\sigma^2=\frac{1}{n}\sum_{i=1}^{n}{\left(x_i-\mu\right)^2\ }}$$ 式(2)
1.2. ボラティリティがある投資のシミュレーションをしよう
それではリターンがばらつく、つまりボラティリティがあることによって投資やギャンブルの結果にどう影響があるのかを見ていきましょう。
あなたの手元に100ドルがあるとします。この100ドルで株を買いましょう。この株は平均で1年に7%値上がりします。10年間後に手元の資金はいくらに増えているでしょうか。平均リターンが7%なので1年後には107ドル、2年後には115ドル、これを10回繰り返すと1.07の10乗で197ドルになると計算できます。素直に考えれば「大体10年で2倍になるのだろう」と皆さんお考えになることでしょう。しかし、そう思って投資をした人の半分以上は肩を落として10年後を迎えることになります。
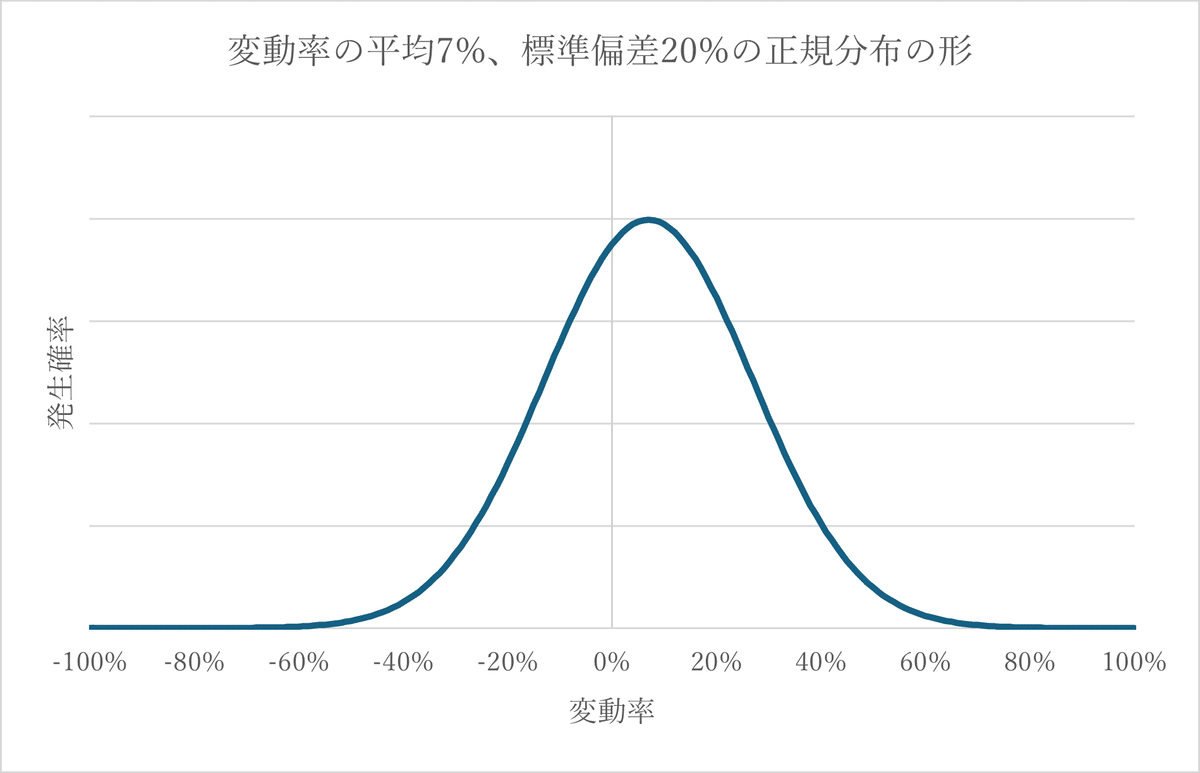
なぜでしょうか。シミュレーションをしてみましょう。投資対象の株は1年に平均して7%値上がりするのですが、同時に標準偏差20%で値上がり率がばらつくとしましょう。ばらつき方にもいろいろ種類があるのですが、ここでは有名な「正規分布」というばらつき方をしているとします。
(解説)正規分布
正規分布はデータのばらつき方の一種です。平均7%で上昇し、標準偏差20%の株の例で考えると1年の変動率は平均の7%になる確率が最も高いのですが、平均から上下1標準偏差(マイナス13%からプラス27%)の範囲に3分の2の確率で収まります。平均から離れた変動率ほど発生する確率は小さくなっていきます。横軸に変動率、縦軸に発生する確率を取って絵を描くと、お寺にある左右対称の釣り鐘のような形になるためベルカーブとも呼ばれます。平均と標準偏差がわかれば正規分布の形は一つに決まるので便利です。正規分布はさまざまな自然現象の発生確率に当てはまるとされており、一番人気のばらつき方です。
マニア向けの本では
$${N\left(\mu,\sigma^2\right)}$$
と書いて、「平均μ、標準偏差σに従う正規分布」を表すので覚えましょう。
1.3. シミュレーションの結果をみよう
では投資の収益が正規分布に従っているとき、投資を続けたあとの資産がどうなるのかをシミュレーションしてみましょう。
1万人の人がそれぞれ100ドルを持って株式に投資することにしました。人々はそれぞれ別の会社の株に10年間投資します。ただしどの株も1年間に平均7%、標準偏差20%の正規分布に従って値段が動くものとします。10年後に1万人の資金はどうなっているでしょうか。
シミュレーションしたところ、1万人の平均では10年後の資産は年率7%の値上がりで予想される200ドルに近い数字になっていました。しかし、200ドルを実現できたのは1万人のうち4000人以下にとどまりました。半分以上の人は平均を達成できなかったのです。5000人以上の人は10年後の資産が170ドル以下という結果になりました。

続けて値上がり率などの他の条件は同じで、標準偏差が50%と高い株に10年間投資した後の1万人の資産をシミュレーションしてみましょう。今回も10年後の平均資産は約200ドルだったのですが、平均を実現できた人数は1万人のうちの4分の1以下になっていました。半分以上の人が資産50ドル以下で10年後を迎えました。毎年平均7%値上がりする株に投資していたのに、半分以上の人は10年後に資産を減らしていたのです。

2つのシミュレーションから、どうやらばらつきの度合い(標準偏差)が大きくなるほど資産の増え方が減る(ひどいときには資産が減っていく)ようだということがわかりましたね。確かに1万人の資産の平均自体は、どちらのシミュレーションでも予想された7%の株価上昇率に見合う水準でした。しかし、多くの人が平均を達成できないとしたら平均など虚しいものでしょう。
このように標準偏差(ボラティリティ)が増加することによって、他の条件が同じなのに運用結果が悪化すること、これがボラティリティタックスです。次の項でボラティリティタックスがどういう仕組みで発生するのかより詳しく見ていきましょう 。
1.4. n年後の投資成果(NAV)の計算式
前の項では株価が毎年平均7%、標準偏差が20%の正規分布に従って動く株に10年投資したときの資産の動きをシミュレーションしました。今度は様々な状況に応用できるような計算方法を考えましょう。株価が1年目には$${r_1%}$$、2年目には$${r_2%}$$、$${i}$$年目には$${r_i%}$$で変動するものとします。すると資産は年々次の倍率で成長していきます。
1年目 $${1+r_1}$$倍
2年目 $${1+r_2}$$倍
3年目 $${1+r_3}$$倍
…….
$${i}$$年目 $${1+r_i}$$倍
…….
$${n}$$年目 $${1+r_n}$$倍
計算を簡単にするために最初の手元資産は1ドルということにします。最初の手持ちが1ドルで毎年$${1+r_i%}$$ずつ株価が変動するので、毎年の倍率をつぎつぎに掛けていけば$${n}$$年後の資産が計算できます(これからは機関投資家っぽくNet Asset Valueの略で「NAV」と言うことにします)。その結果は次の式の金額になります。
$${n}$$年目のNAV$${=\left(1+r_1\right)\left(1+r_2\right)\ldots\left(1+r_n\right)}$$
見やすさを考えてn個のデータの掛け算を表す記号$${\prod_{i=1}^{n}x_i}$$を使うと次のように書き換えられます。「n年目のNAV」もnを添え字にして書きましょう。
$${{NAV}_n}$$=$${\prod_{i=1}^{n}\left(1+r_i\right)}$$
さて、この式をいろいろと加工していくとボラティリティタックスの秘密が明らかになるのですが、ここで2つの大切なテクニックを使います。
1つ目が「式の対数をとる」というテクニックです。
2つ目が「対数関数のテイラー展開」というテクニックです
どちらも少しマニア向けになるので解説します。しっかりと身につけましょう。
(解説)テクニックその1~対数をとる
対数について説明するにはまず「指数」について知ることが近道です。具体的な例で示しましょう。2を3乗すると8になります。数学っぽく書くとこんな感じです。
$${2^3=8}$$
このとき掛けあわせるもとの数2を「底」といいます。「底」を何回掛け算するか(難しい言葉で「べき乗する」といいます)を指示する数3を「指数」といいます。
対数はこの逆で、掛けあわせるもとの数2と結果の数8(「真数」と呼びます)がわかっているとき、何回もとの数を掛け算するとつじつまが合うのかを表す数が「対数」になります。ここでは3です。
底が2、真数が8で対数が3の時のそれぞれの数の間の関係を
$${log_28=3}$$
のように記載します。もとの数が2で結果の数が8のとき、両方のつじつまがあう対数は3になるという意味です。
もとの数と結果の数が同じなら、対数も指数も同じ数字になるのですが、結果の数を求めるための掛け算の回数を指示する数として出てくるときは指数と言い、結果の数と元の数から何回掛け算をすればいいのかを逆算するときは対数と呼びます。(なんだかぺてんにあっているような気がしますね。数学はこんなことが多いので信じてついてきてください。)
特に自然対数、つまり「自然対数の底」を使った対数関数の時には底を省略して$${log2}$$または$${ln2}$$のように記載します(どちらも同じ意味です)。自然対数の底とは約2.71828という具体的な数字になりますが、小数点以下が無限に続いて切りがないのでおしゃれな感じを出すため$${e}$$または$${exp}$$と表記します。$${e}$$や$${exp}$$が出てきたら自然対数のことなので覚えておきましょう。例えば自然対数の底を2乗する場合は$${e^2}$$や$${exp(2)}$$と書きます。
自然対数の底は覚えにくい数値ですが、マニアの間では円周率と同じくらいポピュラーな数値です。とても便利な性質を持つため自然現象や金利計算などいろいろな場面で利用されています。これからこのノートのなかで$${log}$$や$${ln}$$がでてきたときには、特に断りのない限り「自然対数の底」を使い、底を省略して記載します。注意してください。
対数の便利な機能として掛け算を足し算に、割り算を引き算に変換することができることがあります。元の形では扱いにくい式を変換することで計算がしやすくなるときに活用できるのです。掛け算、割り算、べき乗について対数を取ると次のように変換することができます。
$${ln\left(ab\right)=ln\left(a\right)+ln\left(b\right)}$$
$${ln\left(\frac{a}{b}\right)=ln\left(a\right)-\ln{\left(b\right)}}$$
$${ln\left(a^b\right)=b\ ln\left(a\right)}$$
(解説)テクニックその2~テイラー展開
テイラー展開の証明や厳密な成立条件については複雑になるので数学の教科書や参考文献を読んでいただきたいのですが、簡単に述べると、ある関数の特定の点周辺の動きを別の式で表現する方法です。パッと見た感じよくわからない式をテイラー展開で変形するとわかりやすい式になったり、計算が簡単になったりします。
関数が$${y=x^3-6x-3}$$といった場合はあまりテイラー展開で得るものはないのですが、例えば$${y=\cos{\alpha}+\cos{\beta}}$$などのように式を見ただけではどんな動きをするのかパッとわかりにくいような関数の場合、テイラー展開を使って式の形を変えるとわかりやすくなることがあります。$${ln\left(1+x\right)}$$のような対数関数もその一例です。次が関数$${\ln{\left(1+x\right)}}$$をテイラー展開したときの式です。
$${ln\left(1+x\right)=x-1/2x^2+1/3x^3-1/4x^4}$$
$${ln\left(1+x\right)}$$の$${x=0}$$周辺での動きはこの式で置き換える(近似する)ことができると覚えておいてください。ボラティリティタックスのひみつを解明するのに大切な式ですよ。
1.5. ボラティリティタックスの計算方法
さっそく学んだテクニックを使い、1.4で出てきた式(3)の$${n}$$年後の資産($${{NAV}_n}$$)の両辺の対数を取ってみましょう。
$${ln\left(NAV_n\right)}$$=$${ln(\prod_{i=1}^{n}\left(1+r_i\right))}$$=$${\sum_{i=1}^{n}{ln\ \left(1+r_i\right)}}$$ 式(4)
右辺にある合計記号Σの中に対数関数があるのでこれをテイラー展開します。
$${\sum_{i=1}^{n}{ln\ \left(1+r_i\right)}}$$=$${\sum_{i=1}^{n}{(r_i-\frac{1}{2}r_i^2+\frac{1}{3}r_i^3-\frac{1}{4}r_i^4+\ldots)}}$$
更に右辺のシグマ内の関数を項ごとにまとめなおし両辺をnで割ると
$${\frac{1}{n}\sum_{i=1}^{n}{ln\ \left(1+r_i\right)}}$$
=$${\frac{1}{n}\sum_{i=1}^{n}r_i-\frac{1}{2n}\sum_{i=1}^{n}{r_i^2\ }+\frac{1}{3n}\sum_{i=1}^{n}{r_i^3\ }-\frac{1}{4n}\sum_{i=1}^{n}{r_i^4\ }\ldots}$$ 式(5)
になります。
ここで前の話を振り返ります。「1.1ボラティリティの簡単な説明」の(解説)内式(1)で書いた平均の計算法を式(5)と見比べてみましょう。
平均:$${\mu=\frac{1}{n}\sum_{i=1}^{n}x_i}$$ 式(1)再掲
式(5)の両辺が何かしらの平均であることに気付いたでしょうか。式のわかりやすさのために平均の書き方としてμではなくEを使った書き方を活用します。
平均:$${\frac{1}{n}\sum_{i=1}^{n}x_i=E\left[X\right]}$$
この書き方では、株価変動率のように確率でさまざまに動く値$${x_i}$$をひとまとめにして大文字の$${X}$$と書き、その平均を$${E[X]}$$と表現します。式(5)をEを使って書き直すと式(6)になります。(※この大文字$${E}$$は平均の意味で、自然対数の小文字$${e}$$とは全く別なのでとりちがえのないよう注意してください。マニアの間にはこういうまぎらわしいルールが良くありますがくじけず頑張りましょう)
$${E\left[\ln{\left(1+R\right)}\right]=E\left[R\right]-\frac{1}{2}E\left[R^2\right]+\frac{1}{3}E\left[R^3\right]-\frac{1}{4}E\left[R^4\right]\ldots}$$ 式(6)
式(6)の中では1番目の$${r_1}$$から$${n}$$番目の$${r_n}$$をまとめて大文字添え字抜きで$${E[R]}$$と書いて$${n}$$個の数字全部の平均であることを表現しています。
では式(6)の意味を確認していきましょう。右辺ですが、第1項は収益率Rの平均、つまり平均収益率になります。そして第2項は収益率Rの2乗の平均の2分の1、第3項はRの3乗の平均の3分の1になるのです。このパターンで無限に続いていきます。
次に左辺ですが収益率Rに1を足した値(1期間のNAVの成長倍率)の対数を取った値「対数収益率」の平均、「平均対数収益率」になります。
さて、式(4)と式(5)を思い返せばNAVの対数を取って1期間あたりの値に直したものが平均対数収益率でした。平均対数収益率を$${r_{ln}}$$と置けば
$${r_{ln}=E\left[\ln{\left(1+R\right)}\right]=\frac{1}{n}\ln{\left(NAV_n\right)}}$$ 式(7)
になります。
(※またややこしい数学のルールの話をします。Rのようにある数字を大文字で書いたときその数字は競馬の配当金のように様々な値をとる数で、rのように小文字で書いたときは一つの値になる数です。ここでは投資のリターンのように様々な値を取る可能性のある数を大文字Rで、確率がわかれば一つに値が計算できるリターンの平均を小文字rで書いています。)
つまり$${r_{ln}}$$を$${n}$$倍した値を計算し、自然対数の底$${e}$$をその値乗すると$${n}$$期後のNAVになります。式で書けば
$${NAV_n=e^{nr_{ln}}=\left(e^{r_{ln}}\right)^n}$$ 式(8)
でNAVを計算できることがわかります。復習になりますが$${e}$$は2.71828…です。
他方、1期から$${n}$$期までの収益率を合計して割った「普通の」平均収益率を$${r}$$と置きます。
$${r=\frac{1}{n}\sum_{i=1}^{n}r_i=E\left[R\right]}$$
ここで注意ポイントです。最初の資産を1ドルで始める前提で計算しているので$${n}$$期目のNAVは資産が何倍になったかを示しています。したがってNAVから1を引くとn期間を通じた資産の変動率になります。これを$${n}$$で割れば1年あたりの平均収益率になりそうな気がしますが間違いです。さらにいうとこの値は平均対数収益率とも一致しないので注意してください。
$${r\neq\frac{1}{n}\left(NAV_n-1\right)}$$
$${r_{ln}\neq\frac{1}{n}\left(NA\ V_n-1\right)}$$
この数字は「直利」といって投資の成果をはかる物差しとして使うこともありますが、ボラティリティタックスを考えるときには使い道がないので、本ノートではこれまで説明した式(9)の「普通の平均収益率」と式(7)の「平均対数収益率」を使うことにします。
さて話をボラティリティタックスの話に戻します。「毎年の収益率の平均は$${r}$$」と言われたら$${n}$$期後のNAVは
$${NAV_n=\left(1+r\right)^n}$$ 式(10)
になると期待するのは自然なことでしょう。しかしすでに「1.3シミュレーションしてみよう」で見たとおり人々の期待は裏切られます。
式(10)が平均収益率を見て人々が期待するNAVで、式(8)が実際に過半の人が達成できるNAVになります。この2式の差
$${\left(1+r\right)^n-\left(e^{r_{ln}}\right)^n}$$ 式(11)
がNAVベースで見たときのボラティリティタックスです。
NAVベースで考えると投資期間にボラティリティタックスの大きさが影響を受けてしまうので、普通は1期あたりの平均収益率と平均対数収益率の差でボラティリティタックスを把握します。式(6)の左右の項を一部入れ変えた、下記の式(12)が1期あたりのボラティリティタックスになるのです。
$${r-r_{ln}}$$
=$${E\left[R\right]-E\left[\ln{\left(1+R\right)}\right]}$$
=$${\frac{1}{2}E\left[R^2\right]-\frac{1}{3}E\left[R^3\right]+\frac{1}{4}E\left[R^4\right]}$$ 式(12)
1.6. ボラティリティタックスの現実を見てみよう
式(12)でボラティリティタックスの計算方法がわかったので、現実の株の動きで計算してみましょう。今回は、世界で一番人気のあるといっても過言ではない上場型投資信託(ETF)のSPDR S&P500 ETF Trust(SPY)の値段で本当にボラティリティタックスがあるのかを確かめてみることにします。SPYは米国を代表する株価指数のS&P500指数と同じ値動きになることを目指しているETFです。
2018年末から2023年末の5年間のETF価格データから日々の収益率と毎月の収益率を算出して分析対象としました。この期間のSPYの日々の平均収益率は0.0611%でした。平均対数収益率は0.0522%でしたので、その差はマイナス0.0089%になりました。毎日の収益率のデータを使ってボラティリティタックスの式(12)の右辺第3項までの値を計算して合計したところ、0.0089%になりました。現実のデータで調べても平均収益率は平均対数収益率をボラティリティタックス分上回ることが確認できました。

同じ要領で毎月の収益率を計算してみました。すると1か月あたりの平均収益率は1.24292%で、平均対数収益率は1.0953%ということがわかりました。その差はマイナス0.1477%です。こちらも式(12)の右辺第3項までの値を合計した値と一致しました。
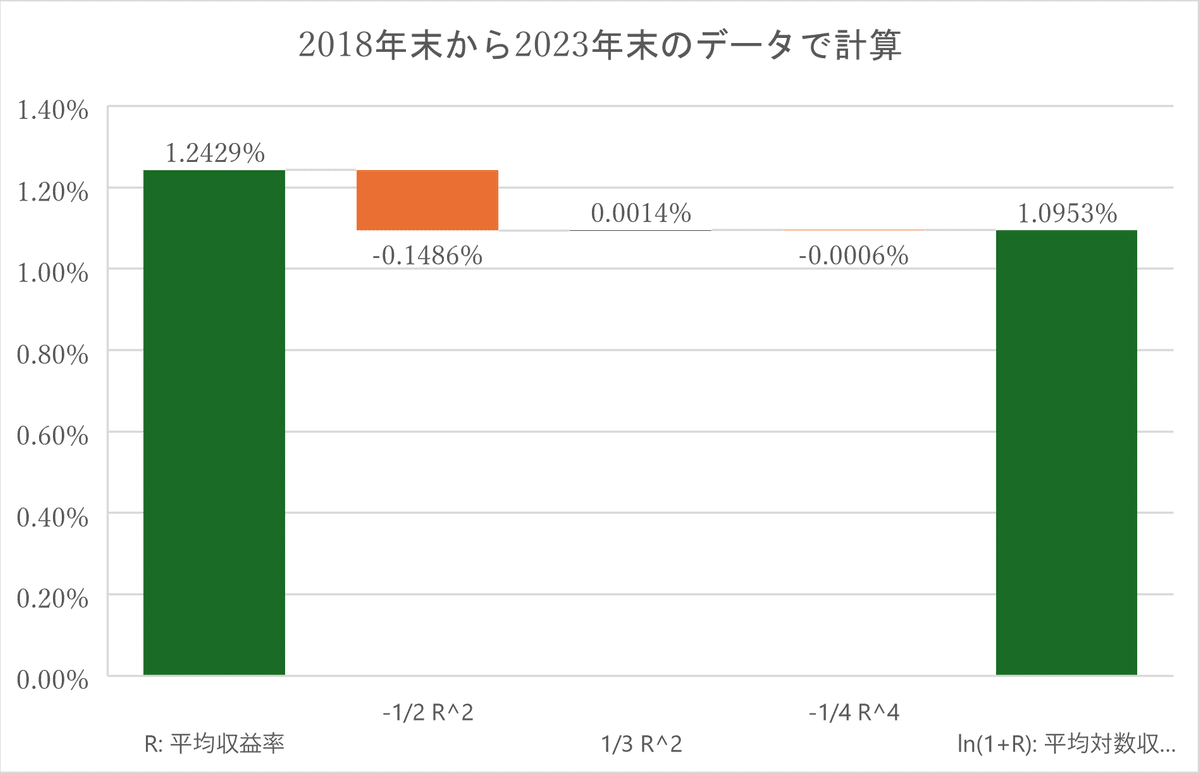
ボラティリティタックスが存在することが現実の取引価格から確認できましたね。
ところでみなさんお気づきでしょうか。日々の収益率で計算しても、毎月の収益率で計算しても、どちらでもボラティリティタックス(平均収益率と平均対数収益率の差)は式(12)の右辺第1項、つまり収益率の2乗の平均の項が大部分を占めています。次の項ではボラティリティタックスが持つさまざまな特徴を見ていきましょう。
1.7. ボラティリティタックスの特徴
改めてボラティリティタックスの式(12)を見てみましょう。
$${r-r_{ln}}$$
=$${E\left[R\right]-E\left[\ln{\left(1+R\right)}\right]}$$
=$${\frac{1}{2}E\left[R^2\right]-\frac{1}{3}E\left[R^3\right]+\frac{1}{4}E\left[R^4\right]}$$ 式(12)再掲
右辺にRの2乗の平均やRの3乗の平均が出てきます。Rを株や商品などの毎日の価格変動と考えると日々の値動きはだいたい1%未満になります。100%未満の小さな値を2乗、3乗するとさらに小さくなっていきます。例えば1%(100分の1)を2乗すると0.01%(1万分の1)になります。Rを3回以上掛ける式(12)右辺第3項以降はゼロに近い数字になっていくと予想できます。「1.6ボラティリティタックスの現実を見てみよう」で観察しましたが、式(12)右辺第1項のR2乗の平均の個所がボラティリティタックスのほぼ全部を占めていた理由はここにあります。そして、収益率の計算期間を毎年から毎月、毎月から毎日と短期間にするほどこの傾向が大きくなることに勘の良い読者はお気づきのことでしょう。そこで、毎日の収益率をベースにしてボラティリティタックスを考えるときは
$${r-r_{ln}=E\left[R\right]-E\left[\ln{\left(1+R\right)}\right]\approx\frac{1}{2}E\left[R^2\right]}$$ 式(13)
と言ってしまっていいでしょう。記号$${\approx}$$は「ほぼ等しい」という意味です。ボラティリティタックスは毎日の収益率の2乗の平均の2分の1にほぼ等しいと言えます。
さて、式(13)でまとめたように収益率Rの2乗の平均部分がボラティリティタックスの本体だということがわかりました。ここで、突然ですが「1.1ボラティリティの簡単な説明」で勉強した式(2)分散の計算を思い返してみましょう。
分散:$${\sigma^2=\frac{1}{n}\sum_{i=1}^{n}\left(x_i-\mu\right)^2}$$ 式(2)再掲
この分散の式を少し展開してみましょう
$${\sigma^2=\frac{1}{n}\sum_{i=1}^{n}\left(x_i^2-2x_i\mu+\mu^2\right)=\frac{1}{n}\sum_{i=1}^{n}x_i^2-\frac{1}{n}\sum_{i=1}^{n}{2x_i\mu}+\frac{1}{n}\sum_{i=1}^{n}\mu^2}$$
定数をn個足してnで割っても元の数と同じなので
$${=\frac{1}{n}\sum_{i=1}^{n}x_i^2-\frac{1}{n}2\mu\sum_{i=1}^{n}x_i+\mu^2}$$
$${x_i}$$の平均$${\sum x_i}$$は$${\mu}$$になるので
$${=\frac{1}{n}\sum_{i=1}^{n}x_i^2-\mu^2}$$
この式を収益率$${r_i}$$について考えると
$${\sigma^2=\frac{1}{n}\sum_{i=1}^{n}r_i^2-\mu^2}$$
これを$${E[ ]}$$を使った書き方にすると
$${\sigma^2=E\left[R^2\right]-E\left[R\right]^2}$$
どうでしょう。どこかで見たことのある形になったのではないでしょうか。そうです。右辺第1項が収益率Rの2乗の平均、つまりボラティリティタックスの本体です。第2項は収益率Rの平均の2乗です。一見どちらも同じ値にみえますが「2乗の平均」と「平均の2乗」で違う値なので注意してください。
2項目の「収益率Rの平均の2乗」に注目しましょう。Rを日々の収益率と考えるとRの平均はよほどのことが無い限りゼロに近い値になります。限りなくゼロに近い値の2乗はどうなるでしょう。これはもうゼロだといってよいでしょう。したがって
$${\sigma^2\approx E\left[R^2\right]}$$
のとおり分散は「収益率Rの2乗の平均」にほぼ等しくなります。このことと式(13)とを合わせて考えると
ボラティリティタックスとは:
$${r-r_{ln}=E\left[R\right]-E\left[\ln{\left(1+R\right)}\right]\approx\frac{1}{2}\sigma^2}$$ 式(14)
になります。ボラティリティタックスは分散の2分の1、つまり標準偏差の2乗の2分の1なのです。
さて、式(8)でn期後のNAVの計算式
$${NAV_n=e^{nr_{ln}}=\left(e^{r_{ln}}\right)^n}$$ 式(8)再掲
を紹介しました。ここでは将来のNAVを予想するのに「平均収益率」ではなくて「平均対数収益率」を使っていることを思い出してください。NAVを左右するのは平均対数収益率なのです。そこで式(14)を、平均対数収益率$${r_{ln}}$$を中心に書き換えてみましょう。
$${r_{ln}\approx r-\frac{1}{2}\sigma^2}$$ 式(15)
おわかりいただけるでしょうか。NAVは「平均収益率」で成長するのではなく、「平均収益率」から分散の2分の1を引いた水準である、「平均対数収益率」で成長するのです。このため、過去の変動率の平均を今後のNAVの成長の予想にそのまま使うと失望的な結果になったというわけです。
n期後のNAVを「平均対数収益率」を使って計算すると式(16)のようになります。
$${NAV_n\approx e^{n\left(r-\frac{1}{2}\sigma^2\right)}}$$=$${\left(e^{r-\frac{1}{2}\sigma^2}\right)^n}$$ 式(16)
「平均対数収益率」$${r-\frac{1}{2}\sigma^2}$$は必ず普通の「平均収益率」$${r}$$よりも低くなりますので、平均収益率だけで計算するとまちがった将来のNAV予想になることがこの式からも見て取れるでしょう。

1.8. 投資比率を変えたらどうなる
前項までで、ボラティリティタックスの計算方法を十分に理解できたと思います。将来のNAVが、普通の収益率の平均ではなく平均対数収益率によって決まること、そして、平均対数収益率は普通の収益率の平均とそのばらつき度合い(標準偏差)によって変動することを勉強しました。「1.2ボラティリティがある投資のシミュレーション」でみたような、平均収益率がプラスなのにNAVがマイナスになってしまう状況は収益率のばらつき度合いが大きくなったことが原因だとわかりました。
さて、はっきりと述べていませんでしたが、ここまでの説明は「持っているお金を全額投資する」という前提で話を進めてきました。しかし現実では必ずしも有り金全てをリスクのある資産への投資に回す必要はありません。競馬の好きな人でも毎回のレースに常に全額を賭ける人はあまりいないでしょう。レースごとに賭ける金額を動かすというのは実は大切な戦略なのです。手元の資金のうちどのぐらいを賭けに(投資に)回すのがいいのかについてはじつは客観的かつ具体的に決めることができます。この項では一番いい投資比率の決定方法についてみていきましょう。驚くべきことに最適な投資比率の決定方法はボラティリティタックスと密接な関係があるのです。
持っているお金を全額投資している状態はすなわち投資比率が100%の状態です。多くの人は持っているお金のうち投資にあてるのは20%か30%くらいでそのほかは定期預金に預けたり、現金で持ったりしていることでしょう。このとき預金した部分にはわずかですが金利がつきます。また、人によっては投資比率が100%超え、つまり借金をして投資をしている人がいるかもしれません。この時は逆に借りたお金の金利を払わなければいけません。さらに、投資比率がゼロ%未満の場合も考えられます。これは、誰かから株などを借りて売っている状態です。このときは手元の資金に加えて売った株の代金の金利が受け取れますが、借りた株の借り賃を払わねばなりません。
このように投資比率を100%以外にすると、借りたお金や余ったお金の金利などを考える必要がありややこしくなるのですが、むつかしいことを考える前にとりあえずは金利などの費用が無い状態でどうなるのか見ましょう。
まず投資する株式の$${i}$$期の収益率を$${r_i}$$とします。次に、手元資金のうち株式に投資する比率を$${f}$$と置きます(投資比率を表す記号には伝統的に割合を意味するfractionの$${f}$$を使います)。余った資金を預けた時や、信用取引で借りた時の金利を$${r_d}$$とします。手持ち資金の一部を投資したとき、第$${i}$$期の収益率は
$${fr_i+\left(1-f\right)r_d}$$
になります。いったんは金利が無い$${r_d=0}$$の状態で考えるので資金の一部を投資したときの収益率を
$${fr_i}$$
とします。
繰り返しになりますがNAVを決めるのに大切なのは「平均対数収益率」なので、この収益率から、「1.5ボラティリティタックスの計算方法」のところで行った計算を参考に「平均対数収益率」を計算します。
具体的には式(6)のn$${R}$$を$${fR}$$で置き換えます。大文字の$${R}$$は確率に従って様々に動く$${r_i}$$をまとめて表す書き方です。
$${E\left[\ln{\left(1+fR\right)}\right]=E\left[fR\right]-\frac{1}{2}E\left[f^2R^2\right]+\frac{1}{3}E\left[f^3R^3\right]-\frac{1}{4}E\left[f^4R^4\right]}$$
「1.7ボラティリティタックスの特徴」と同様に、ゼロ近辺で動く収益率を3乗した値はほぼゼロとみなしてしまいましょう。さらに、$${f}$$は定数なので平均計算の$${E}$$の外に出します。
$${E\left[\ln{\left(1+fR\right)}\right]\approx fE\left[R\right]-\frac{1}{2}f^2E\left[R^2\right]}$$
この式の右辺は見覚えのある部分がばかリですね。左辺の投資比率$${f}$$の時の平均対数収益率を$${r_{fln}}$$と書くことにします。$${E[R]}$$は収益率の平均$${r}$$です。$${E[R^2]}$$は収益率の分散$${\sigma^2}$$で置き換え可能です。これらの記号を使って上式を書くと
$${r_{fln}\approx fr-\frac{1}{2}f^2\sigma^2}$$ 式(17)
のとおりになります。これで手持ち資金の一部を投資に回した時の平均対数収益率が出たので、式(8)を使ってn期後のNAVが計算できます。
$${NAV_n=\left(e^{fr-\frac{1}{2}f^2\sigma^2}\right)^n}$$ 式(18)
この式でNAVに影響を与えるのは、収益率の平均$${r}$$と分散$${\sigma^2}$$、投資期間$${n}$$、そして手元資金のうちどれだけを投資するかの$${f}$$です。そこで平均、分散、投資期間を一定にしたときの投資比率$${f}$$とNAVの関係を見て見ましょう。
次の図のように、投資比率をゼロから高めていくとNAVもしばらく増加していくのですが、あるところでピークを迎えます。この事例では投資比率0.8(80%)あたりでNAVが最大になり、それ以上投資比率を上げるとNAVはどんどん小さくなっていくのです。プラスのリターンの投資であってもむやみに投資していればいいというわけでないことがわかるでしょう。一番いい投資の割合というのが存在するのです。

ではどうやって一番いい投資割合をみつけることができるでしょうか。式(18)を見てわかるようNAVが最大になるのは、式(17)で示した平均対数収益率が最大になるときです。したがって、平均対数収益率が最大になる投資比率が一番いい投資割合になります。

どうでしょう。確かに平均投資収益率が最大になっているときの投資比率でNAVも最大になっている気配が感じられますね。0.8ぐらいだけど正確にはいくつでしょうか。きちんと投資比率を特定するのに役立つのが「微分」というテクニックです。
1.9. 微分でベストな投資比率をみつけよう
微分は滑らかな曲線で描くことのできる関数を細かく区切って分析していく方法です。正確さを二の次にしてわかりやすく説明すると、調べたい関数をルールに従い加工して、元の関数の曲線上の角度(「傾き」といいます)を計算する別の関数にするテクニック、それが微分です。
例えば上の平均対数収益率と投資比率のグラフでは、投資比率がゼロから大きくなっていくに従い傾きはどんどん小さくなっていきます。あるところで傾きはゼロになりその後はマイナスになります。気が付いたでしょうか。微分した関数の値がゼロ、つまり元の関数の傾きがゼロのところ見つけるとその点で元の関数は最大値をつけるのです。(※この微分の説明はわかりやすさ重視で不正確です。詳しいことを知りたい人は高校の教科書を参照してください)。
なお途中で切れていたり、角になって折れ曲がっている関数は微分できないので注意してください。先ほどの平均対数収益率$${\mu_{fln}}$$と投資比率$${f}$$の関係の図をみたかんじどうやら微分できそうですね。
さて、具体的な微分の方法ですが手っ取り早く公式を使いましょう。今回は一番基本的な次の公式だけで用が足ります。微分対象の関数が
$${y=ax^b}$$
の形のときこの関数を$${x}$$について微分すると
$${\frac{dy}{dx}=abx^{b-1}}$$
になります。$${\frac{dy}{dx}}$$というのは関数$${y}$$を$${x}$$について微分するというマニアの書き方です。割り算でも分数でもないので注意してください。
準備ができましたので平均対数収益率と投資比率の関係を表した式(17)を微分してみましょう。忘れているかもしれませんのでリマインドすれば微分の目的は、平均対数収益率が最大(つまりNAVが最大)になるような投資比率$${f}$$をみつけることです。
$${r_{fln}\approx fr-\frac{1}{2}f^2\sigma^2}$$ 式(17)再掲
これを$${f}$$について微分すると
$${\frac{dr_{fln}}{dx}\approx\ r-f\sigma^2}$$
になります。これがゼロになるのは
$${f=\frac{r}{\sigma^2}}$$ 式(19)
が成り立つときだけです。「普通の」収益率の平均が高いと、高い投資比率が有利になり、収益率の分散が大きいと投資比率を下げた方が良いという関係です。普通の収益率の平均をその分散(標準偏差の2乗)で割った値の投資比率で投資をしたときに平均対数収益率が最大に、つまりNAVが最大になるのです。ここまでわかれば最適投資比率の時の平均対数収益率も計算できますね。式(17)の$${f}$$に式(19)を入れて見ましょう。
$${r_{fln}\approx\frac{r}{\sigma^2}r-\frac{1}{2}\left(\frac{r}{\sigma^2}\right)^2\sigma^2=\frac{1}{2}\left(\frac{r}{\sigma}\right)^2}$$ 式(20)
どうですか。右辺の括弧内を見て見ましょう。普通の収益率を標準偏差で割った値になります。これを2乗して半分にすると最適投資比率での平均対数収益率です。これが達成できる最大の収益率レベルということになるのです。
ところで、式(20)の中に出てくる「普通の収益率を標準偏差で割った値」ですが、これはマニアの間で(金利がゼロのときの)「シャープレシオ」と呼ばれる数値です。シャープレシオはアメリカの偉い先生が考えた投資の成果をはかる物差しで、投資信託の運用成績のよしあしを考えるときに使ったりします。かっこいい言い方では「リスクの市場価格」とも言います。投資比率を工夫して出せる最大の収益率というのがリスクの市場価格で決まってくるなんて神の見えざる手が働いている感じがしますね。
1.10. 金利のある時はどうなる
1.9では金利がゼロ、つまり全額を投資に回さないで余ったお金を銀行に預けても金利を受け取れず、持っているお金以上の株を買うために借金しても金利を払う必要が無い、という前提で投資比率を変えると投資成果がどう変わるのかみてきました。
今回はより現実に近づけるために預けたお金、借りたお金どちらにも金利が発生することを前提として最適な投資比率を考えることにしましょう。分析には1.8で使った投資比率$${f}$$、金利$${r_d}$$のときの収益率
$${fr_i+\left(1-f\right)r_d}$$
今回も確率でいろいろ動く$${r_i}$$を大文字の$${R}$$でまとめ表現した
$${fR+\left(1-f\right)r_d}$$
を使います。今回は金利$${r_d}$$をゼロにしないで話を進めましょう。次に、「1.5ボラティリティタックスの計算方法」のところで使った式(6)を再び参照します。
$${E\left[\ln{\left(1+R\right)}\right]=E\left[R\right]-\frac{1}{2}E\left[R^2\right]+\frac{1}{3}E\left[R^3\right]-\frac{1}{4}E\left[R^4\right]}$$ 式(6)再掲
この$${R}$$を、手持ち資金の一部だけを投資し金利を考えたときの収益率$${fR+\left(1-f\right)r_d}$$で置き換えます。また、「1.7ボラティリティタックスの特徴」の時と同じく、収益率はだいたいゼロ近辺の値を取ると考えれば、右辺第3項以降はほぼゼロになるので式から取り除きます。
$${E\left[\ln{\left(1+R\right)}\right]\approx E\left[fR+\left(1-f\right)r_d\right]-\frac{1}{2}E\left[\left(fR+\left(1-f\right)r_d\right)^2\right]}$$
右辺のカッコ内を展開すると
$${=E\left[fR+\left(1-f\right)r_d\right]-\frac{1}{2}E\left[f^2R^2+2\left(1-f\right)fr_dR+\left(1-f\right)^2r_d^2\right]}$$
収益率$${R}$$以外は一つの値になる定数なので$${E[ ]}$$の外に出すことができます。
$${=fE\left[R\right]+\left(1-f\right)r_d-\frac{1}{2}f^2E\left[R^2\right]-\left(1-f\right)fr_dE\left[R\right]-\frac{1}{2}\left(1-f\right)^2r_d^2}$$
見やすくするためにこの式を$${r}$$(収益率の平均)と$${\sigma^2}$$(収益率の分散)を使って書き直しましょう。$${E\left[R\right]=r}$$で、$${E\left[R^2\right]=\sigma^2}$$でしたね。
$${=fr+\left(1-f\right)r_d-\frac{1}{2}f^2\sigma^2-\left(1-f\right)fr_dr-\frac{1}{2}\left(1-f\right)^2r_d^2}$$
さて、収益率の平均$${r}$$と金利$${r_d}$$はどちらも相当ゼロに近い値です。ゼロに近い値を2乗した値や掛け合わせた値は限りなくゼロに近くなり無視できることにしましょう。するとこの式は
$${=fr+\left(1-f\right)r_d-\frac{1}{2}f^2\sigma^2}$$
投資比率$${f}$$でまとめると
$${=r_d+f\left(r-r_d\right)-\frac{1}{2}f^2\sigma^2}$$
と書くことができます。
投資比率$${f}$$がいろいろ変わるときの平均対数収益率を$${r_{fln}}$$と置けば
$${\mu_{fln}\approx r_d+f\left(r-r_d\right)-\frac{1}{2}f^2\sigma^2}$$ 式(21)
になります。「1.9微分でベストな投資比率をみつけよう」で行ったのと同じようにこの式を投資比率$${f}$$について微分してみましょう。
$${\frac{dr_{fln}}{df}=\left(r-r_d\right)-f\sigma^2}$$
これがゼロになるときの投資比率$${f}$$は
$${f=\frac{r-r_d}{\sigma^2}}$$ 式(22)
です。普通の収益率$${r}$$から金利$${r_d}$$を引いた「超過収益率」を分散$${\sigma^2}$$で割った投資比率で投資したときに平均対数収益率が最大になるのです。超過収益率と分散の関係次第で、手持ち資金の範囲内で投資(現物取引)するのが最適であったり、お金を借りて手持ち以上に投資(信用取引)するがの最適であったりします。また超過収益率がマイナスの時は投資比率がマイナスになりますがこれは空売りが最適な取引ということを意味しています。
続けて金利があるときに達成可能な最大の平均対数収益率を計算してみましょう。
$${r_{fln}\approx r_d+\frac{1}{2}\left(\frac{r-r_d}{\sigma}\right)^2}$$ 式(23)
これが投資比率をいろいろ工夫して達成できる最大の収益率になるのです。この式の右辺括弧内に注目しましょう。超過収益率を標準偏差で割った値です。これは金利を考えた時の「シャープレシオ」つまりリスクの市場価格です。金利を考えた時もやはり達成できる最大の収益率はリスクの市場価格によって決まるのです。
1.11. 現実の最適投資比率とケリーの公式
これまであたかもオリジナルのアイデアかのようにNAV(平均対数収益率)を最大にする投資比率の計算方法を書いてきましたが、どれも1950年代以降いろいろな人が研究してきた成果です。最初の研究は、1957年にジョン・ケリーという人がコイン投げを題材にして、持ってきたお金のどれくらいを賭けるのがいいかを考えたことに始まります。その後いろいろな人が研究を進めて投資にも応用できるようになりました。詳細についてはKellyやThorpeなどの優れた研究を参照していただきたいのですが、式(22)のような手持ち資金のどれくらいを投資するのが最適なのかを計算する式は、先駆者をリスペクトして「ケリーの公式」(Kelly criterion)と呼ばれています。
この項ではケリーの公式で計算した投資比率を使うと本当に投資収益(NAV)が最大化になるのか、現実の株価の動きを対象にして調査することにします。「1.6ボラティリティタックスの現実を見てみよう」で使ったS&P500指数に連動することを目指すETFのSPDR S&P500 ETF Trust(SPY)の価格を実例として使用します。
2019年から2023年の5年間を対象に計算すると、SPYの日次リターンの算術平均は0.0611%(年率15.4%)、その標準偏差は1.3267%(年率21.1%)になります。無リスク金利を日次0.0198%(年率5%)とすると、(式22)で得られる最適投資比率は2.344になりました。
2019年から2023年までの4年間にわたりいろいろな投資比率でSPYに投資したときの資産の状況(NAV)を計算してみました。たしかに投資比率2.3から2.4の間で運用後の純資産が最大になるようです。なお投資比率が1以上というのはお金を借りて手持ち資金以上の投資、つまり信用取引をしている状態です。2019年から2023年のSPYの場合はお金を借りてでも投資をした方が良かったということになります。

続けていくつかの投資比率で投資したときの時系列のNAVの推移をみて見ましょう。投資比率0.5、1.0、2.3、3.0について2018年末(スタート時点)から2023年末までのNAVの推移を計算しました。投資比率を上げるほど資産の変動が大きくなっていきますが、最終的なNAVは最適投資比率の2.3をピークに低下します。予想通り最適投資比率を超えてリスクを取っても収益面では意味がないのです。

1.12. まとめ
最後にボラティリティタックスについてわかったことをまとめておきましょう。
ボラティリティタックスとは平均収益率と平均対数収益率の差。
平均対数収益率$${r_{ln}}$$は常に平均収益率$${r}$$を下回る。
将来のNAVを決めるのは平均対数収益率であって平均収益率ではない。
ボラティリティタックスはだいたい収益率の分散(標準偏差の2乗)の2分の1になる。
ボラティリティタックスは常に運用成績にマイナスになる。
平均収益率が同じでもその分散(ばらつき度合い)が大きくなるほどボラティリティタックスが大きくなり運用成果が悪化する。
そのため「ケリーの公式」を使ってちょうどいい投資比率を具体的に決めることができる。
以上でボラティリティタックスの仕組みがなんとなく理解できたのではないかと思います。次のノートでは、ボラティリティタックスと同じ原因で発生する「レバレッジファンドの減価」について詳しくみながら、ボラティリティがパフォーマンスに与える影響を違った側面から学習しましょう。
