
自作数学問題解説#1
こんにちは、ぱぺです。
数学の問題を作ったので生存報告の代わりとして解説を含め上げてみます。
ちなみにこれ下書きの途中で放置してたので作ったのは2ヶ月くらい前です。
【問題】
使う内容:A(合同式), II(多項式計算・複素数と方程式)

数ヶ月前に作った問題の式などを変えて、(4)を新たに付け足しました。
以下解答・解説があります。
【解答1】
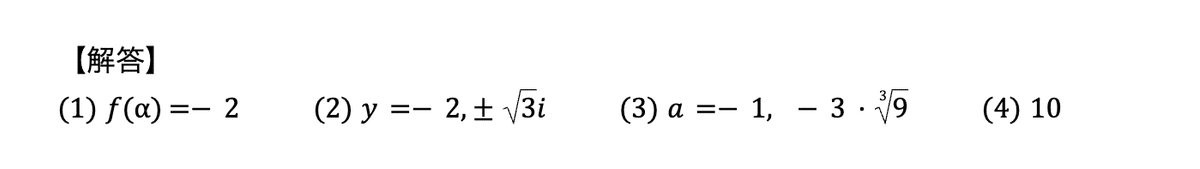
(1)~(3)は整式の剰余と方程式、(4)は合同式などをうまく使います。
【解説1】
(1)
f(x)をh(x)で割った割り算を f(x)=Q(x)h(x)+R と表すとすると、
h(α)=0であるからx=αを代入してf(α)=Rを導ける。
つまり整式の剰余を用いて6次式から2次以下の式へと、
代入の手間を省くことができる。

今回は「 奇 跡 的 に 」(ここ重要)剰余項が定数;。
αの値を求める必要なく済んだ。よかった。
(2)
(1)で作った式から (因数分解された形)=0の形を作れる。
ここから解が条件に合うか吟味していく。
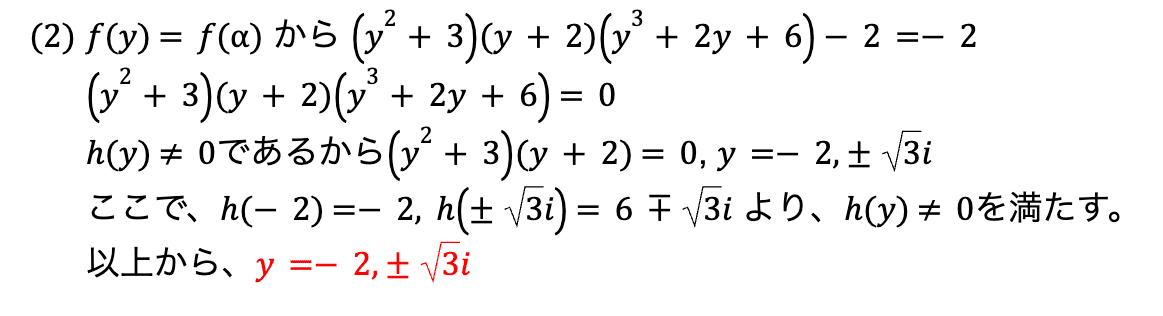
(3)
x³+ax+6=0について
それが2重解をもつ
そのどれかの解が他の解と一致する
の2つの場合に分けて考えればよい。
解と係数の関係は、方程式が2重解を持つように係数をいじる時にものすごく便利である。
解答するときは3乗根の3が前の3にかかって-(3^3)√3=-27√3と見えてしまわないよう気をつけること。または指数表記で- 3^(5/3)としてしまえば良い。

(4)
①から f(-2)=-2 であり、nを13で割った余りが-2であることから、この厳つい式はmod13で計算・変形することで簡単な等比数列の和へと変化する。
(整数)/3型の整数(以降c)の余りを求めるには、まず分子3cの余りを計算し、
3c≡4(mod13)
の形から、cを13で割った余りを求めることにしよう。

以降 3c ≡ 4 (mod 13)からcの余りを導く解答である。
解法分岐①
両辺を9倍してmod13をすると、
3で割ることなくcの余りを求めることができる。
27c ≡ 13·2c+c ≡ c (mod 13)
36 ≡ 13·2+10 ≡ 10 (mod 13)

解法分岐②
13で割ると4余る3の倍数を見つけることで、そこから13と互いに素な整数3で単純に割ることができる。
3c ≡ 4+13·2 (mod 13)
3c ≡ 3·10 (mod 13)
3と13は互いに素より c ≡ 10 (mod 13)

解法分岐③
cが整数であることから分子=の形にして
一次不定方程式3c=13d+4 (c,dは整数)を解こうとすると、
c-10が13の倍数だとわかる。

〆。
あとはもう答えが出たも同然。
求める余りは10である。

【あとがき】
この記事書き始めたの2ヶ月は前です。惰性、よくない。
最近作問のネタが尽きてきているのでここからさらに時が開きそうです。
がんばります。
