
【MATLAB】計算の高速化のためにボトルネックを発見する方法~プロファイラーでパフォーマンスを評価~
数値計算を目的としたコードは「もっと高速化したい!」となります。そのような場合、計算時間が長いボトルネックとなっている箇所を見つけ、そこを改良して短くすることが有効な方法の1つです。
ここで重要なのは「どこが計算時間が長くなっているか」を見つける方法です。簡単なコードであれば直ぐに見つけることができますが、複数の関数を参照するような複雑なコードになるほど見つけることが大変になります。
MATLABでは計算時間が長い箇所を見つけるときに便利な機能があるので、その使用方法をまとめました。
1. コードのプロファイリング機能
今回使用する機能は、プロファイリングです。簡単に紹介すると、コードを実行して評価することで関数やコード行の計算時間や、最も頻繁に呼び出されるものを調査する機能です。この機能は、
プロファイリング機能を有効にする。
分析したいコードを実行する。
計算時間や呼び出し回数を確認する。
という手順で誰でも簡単に使えます。詳細は、公式のドキュメントが非常にわかりやすいです。
https://jp.mathworks.com/help/matlab/matlab_prog/profiling-for-improving-performance.html
また、公式よりYouTubeにも使用する動画が上がっています。
今回は、適当な数値計算の関数を用意して、その関数に対してプロファイリングを行い、ボトルネックの部分を調べてみます。
2. 実際に使用してみた
【検証に使用するコード】
検証用の数値計算の関数を以下のように作成しました。簡単に説明します。
function totalResult = mainComputation(n, useVectorized)
% mainComputation:
% 複数のサブ関数を組み合わせた数値計算を実施するメイン関数です。
% 引数 n: ループ回数(デフォルトは 10)
% 引数 useVectorized: true の場合は累積二乗和の計算にベクトル化版を使い、
% false の場合は for ループ版を使用(デフォルトは false)
%
% この関数内では、heavyFunction と lightFunction を呼び出し、
% また、累積二乗和計算関数(cumulativeSquareSum_loop / _vectorized)も利用します。
if nargin < 1
n = 10; % デフォルトの反復回数
end
if nargin < 2
useVectorized = false; % デフォルトは for ループ版を使用
end
totalResult = 0;
% 重い計算処理を行う関数を呼び出す(内部で subHeavyFunction を利用)
heavyVal = heavyFunction(5);
% メインの for ループ
for i = 1:n
% ここでは、1 から i までの累積二乗和を計算します。
% for ループ版とベクトル化版の両方を用意しています。
x = 1:i; % 累積計算の対象ベクトル
if useVectorized
cumSumVec = cumulativeSquareSum_vectorized(x);
else
cumSumVec = cumulativeSquareSum_loop(x);
end
% 累積二乗和の最終値(すなわち sum(x.^2))を利用
cumSumVal = cumSumVec(end);
% 各ループごとに、上記3つの結果を合算
totalResult = totalResult + heavyVal + cumSumVal;
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% heavyFunction: 重い計算処理を実施(内部で subHeavyFunction を呼び出す)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function heavyVal = heavyFunction(x)
% heavyFunction:
% 大量の for ループとサブ関数の呼び出しにより、
% 計算負荷の大きい処理をシミュレーションします。
%
% heavyFunction 内で、subHeavyFunction を複数回呼び出し、結果に sin を適用します。
heavyVal = 0;
% 例として 1~100 のループを回し、各ループで subHeavyFunction を呼び出す
for j = 1:100
heavyVal = heavyVal + sin(subHeavyFunction(x, j));
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% subHeavyFunction: heavyFunction 内で呼び出されるさらに重い計算処理の関数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function y = subHeavyFunction(a, b)
% subHeavyFunction:
% 引数 a, b を用い、複数回の for ループによる計算処理を実施します。
% ここでは cos を用いた単純な計算を複数回行い、計算負荷を上げています。
y = 0;
% 例として 1~50 のループを回して計算
for k = 1:50
y = y + cos(a + b + k);
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% cumulativeSquareSum_loop: for ループ版 累積二乗和計算関数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function result = cumulativeSquareSum_loop(x)
% cumulativeSquareSum_loop:
% 入力ベクトル x の各要素までの二乗和(累積二乗和)を
% for ループを用いて逐次計算します。
%
% 例:
% x = [1, 2, 3, 4];
% result = [1, 1+4, 1+4+9, 1+4+9+16] = [1, 5, 14, 30]
n = length(x);
result = zeros(1, n);
for i = 1:n
tempSum = 0;
for j = 1:i
tempSum = tempSum + x(j)^2;
end
result(i) = tempSum;
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% cumulativeSquareSum_vectorized: ベクトル化版 累積二乗和計算関数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function result = cumulativeSquareSum_vectorized(x)
% cumulativeSquareSum_vectorized:
% 入力ベクトル x の各要素までの二乗和(累積二乗和)を
% ベクトル演算(cumsum と要素ごとの二乗)を用いて計算します。
%
% 例:
% x = [1, 2, 3, 4];
% result = [1, 5, 14, 30]
result = cumsum(x.^2);
end
合計で5個の関数があり、依存関係は以下のようになっています。ちなみ依存関係の図はMATLABの依存関係機能を使用することで可視化できます。(この機能もコードの規模が大きくなるほどかなり便利)
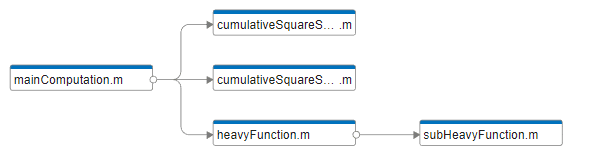
関数 mainConputationから3つに分岐している。この関数は「forループを使用」「ベクトル化を使用」に切り替えることができるように作成した。MATLABでは、高速化のためにベクトル化することがしばしば用いられる。その切り替えのために、
関数 cumulativeSquareSum_loop: forループバージョン
関数 cumulativeSquareSum_vectorized: ベクトル化バージョン
を作成した。関数heavyFunctionは、関数subHeavyFunctionを呼び出し、forループを使用する関数である。関数の呼び出し回数の評価のために用意した。関数 mainConputationの引数に入力する値が大きいほど、関数 cumulativeSquareSum_loopと関数 cumulativeSquareSum_vectorizedの計算時間の差が大きくなります。
次に、関数を以下のコードで実行します。
clear;
clc;
% 計算の反復回数 n を設定
n = 1000;
%% forループ版を使用(useVectorized = false)
disp('*** テスト:forループ版(useVectorized = false) ***');
tic;
result_loop = mainComputation(n, false);
time_loop = toc;
fprintf('結果: %f\n', result_loop);
fprintf('実行時間: %f 秒\n', time_loop);
disp('----------------------------------------');
%% ベクトル化版を使用(useVectorized = true)
disp('*** テスト:ベクトル化版(useVectorized = true) ***');
tic;
result_vectorized = mainComputation(n, true);
time_vectorized = toc;
fprintf('結果: %f\n', result_vectorized);
fprintf('実行時間: %f 秒\n', time_vectorized);
disp('----------------------------------------');
%% 結果の比較
if abs(result_loop - result_vectorized) < 1e-10
disp('結果は両バージョンで一致しました。');
else
disp('結果に差異があります。');
endプロファイリング機能を有効にしたのちに、forループバージョンとベクトル化バージョンでそれぞれ分析を行います。
【分析の手順】
①MATLABのアプリの一覧から「プロファイラー」のアイコンをクリックして起動します。


②プロファイル開始で分析を開始後、分析したいコードや関数を実行します。
今回は画像のようにセクション区切りをすることで、2つのバージョンで分析をしました。

コードを実行すると、プロファイルウィンドウの分析開始アイコンが赤くなります。分析したいコードの実行が終了したら、アイコンをもう一度クリックして分析を終了します。

③分析結果を見て計算時間や呼び出し回数を確認します。

【分析結果を見る】
forループバージョンの結果を見てみます。プロファイラーの結果をみると、上の方に横バーが積み重なった図があります。水色の部分がメインで実行した部分です。バー内の文字を見ると関数名が表示されています。今回は、最初に関数 mainConputationをクリックして開いてみます。

開くと「最も時間を要する行」「呼び出される関数」「各行ごとに計算時間が表示された結果」が載っています。まず「最も時間を要する行」が以下の通りです。


呼び出し回数、各行の計算時間、計算時間が関数の計算全体でどのくらいの割合かが表示されます。今回は、引数の回数だけ呼び出される関数 cumulativeSquareSum_loop が計算時間のほとんどを占めていることがわかります(合計8.010秒に対して8.003秒要している)。
次に「呼び出される関数」です。

こちらも同様に計算時間などが表示されます。違いは、行ではなく、関数内で呼び出される関数のみの結果を示す点です。次に「各行ごとに計算時間が表示された結果」です。

赤字が計算時間、青字が呼び出される回数です。また、コード内で計算時間が長い行ほど、濃い赤色でハイライトされます。引数に応じてforループが変化する関数であるため、forループ内の行は1000回ずつ呼び出されるていることが確認できます。
ここなで示した結果は、forループバージョンの結果です。やはり、関数 cumulativeSquareSum_loop がボトルネックになっていると言えます。この部分をベクトル化で処理するようにした場合(ベクトル化バージョン)の結果を見てみます。「最も時間を要する行」の結果です。

まず、右端をみると、forループバージョンと比較してコード全体で計算時間の差が小さくなっていることがわかります。計算時間も関数全体で0.008秒、関数 cumulativeSquareSum_vectorizedで0.004秒と大幅に計算時間が短くなっていることがわかります。次に「各行ごとに計算時間が表示された結果」でう。

forループバージョンと比較して、赤くハイライトされている箇所が増えています。これは計算時間が増加したわけではなく、関数cumulativeSquareSum_vectorizedの計算時間が短くなったことでコード全体の差が小さくなり、他の行の割合が増えたのでこのような結果となっています。
このように計算時間や呼び出し回数をすばやく比較できるため、簡単にボトルネックの箇所を見つけることができます。
3. さいごに
今回はコード分析機能を使用して、計算のボトルネックとなっている箇所を見つける方法を紹介しました。
私は研究で提案手法の実装時に、この機能を使用してボトルネックとなっている箇所を最適化していくことで、計算時間を100倍以上高速化できました。MATLABで数値計算を実装する上で必須機能だと感じています。
また、MATLABにおいてベクトル化の有効性が非常にわかりやすい例だったと思います。
以上!!!!!!!
見出し画像の作成にあたり以下のサイトのアイコンを使用させていただきました。
【前の記事】
このコードも今回の機能を使いながら実装しました。
【次の記事】
(未定)
