【読了】医療統計 データ解析しながらいつの間にか基本が身につく本 Stataを使ってやさしく解説
正誤表 https://www.yodosha.co.jp/correction/9784758123792_correction.pdf
序
臨床研究をしたい場合に勉強すること
・統計
・疫学
・研究デザイン
・統計アプリの使い方
本書では臨床研究を行うために最低限必要なトピックのみに絞る
・臨床疫学
・生物統計
・統計アプリ(Stata)
▼講義編
講義編を読む前に
学会発表
演題
論文投稿
抄録(abstract)
PICO(介入研究)/PECO(観察研究)
P:Patient(患者)
I/E:Intervention(介入)/Exposure(曝露)
C:Comparison(比較対照)
O:Outcome(結果)
PICOは介入研究、PECOは観察研究で用いられることになります。
IとEを理解する上で重要なのは、Iは"患者に対して積極的な介入を行う"のに対し、Eは"曝露要因があるかないか"で患者を分類する点です。
IとEが同じ「1週間に200 g以上のアルコール摂取」であったとしても、もともとアルコールを摂取しない人にアルコールを摂取させているのであれば、これは「介入」なので「I」になります。一方、研究を開始する前からアルコールを200 g/週以上摂取している人を対象とするのであれば、これは介入ではなく「曝露」であり、「E」に該当します。
研究手法からも考えてみましょう。介入研究では、特定の介入の影響を評価するため、「PICO」が用いられます。観察研究であれば、特定の要因への曝露を検討するため、「PECO」が用いられることになります。
研究計画が作成できたら、倫理委員会に倫理審査を依頼して、カルテからデータを収集する
第1章 私たちは,なぜ臨床研究をするのか?
日々の疑問(CQ、クリニカルクエスチョン、世界中の医療従事者が現場で抱いた臨床上の疑問)を解決するため
現場の問題は、現場の医療従事者にしか気づけない(臨床研究の専門家には気づけない)し、解決もできない
臨床研究は、CQをRQ(リサーチクエスチョン)に落とし込むところから始まる
臨床研究の特徴
①観測が困難
・とても稀な症例
・検査にかかる費用が研究費から捻出できない
・すべての関連情報を事細かく記録できない(SES:社会経済状況、など)
・そもそも測定方法がない(未知の感染症など)
・測定誤差
・偶然誤差
・系統誤差:測定機器や測定スタッフが異なるため誤差がある
・過失誤差:入力ミスや入力忘れにより、外れ値や欠損値がある
②時間の要因が重要
回復退院できたという観点では同じでも、3日で回復した場合と、回復に3カ月かかった場合では区別するべき
④倫理的な問題
第2章 臨床研究の流れ
疑問の定式化
①クリニカルクエスチョン
②文献検索:既知と未知を把握する
③リサーチクエスチョン:PECO/PICO・研究デザインで定式化する
④FINERチェックリストにかける:必要に応じて文献検索に戻る
研究計画書の作成
研究の目的・方法/収集するデータ・サンプルサイズ(症例数)/採用する統計解析方法
倫理委員会による審査
略
研究の実施
①データ収集計画の作成:質の良いデータを取れるように工夫する
②データ収集
データ分析
①データクリーニング
②統計解析
学会発表
略
論文作成
論文として文書化して初めて後世の研究者の役に立つ、1つの研究で明らかにできることには限界がある
第3章 PICO/PECO+研究デザイン
PICO/PECO+研究デザイン
疑問を定式化するフレームワーク
・P(Patient, Problem):糖尿病を患う中年男性が
・I/E(Intervention / Exposure):有酸素運動をすることは
・C(Comparison, Control):運動しないことに比べて
・O(Outcome):心疾患イベントの予防に効果があるか?
・代理アウトカム(主要アウトカムよりも症例数が多いものを設定する):血圧の低下に効果があるか?
・研究デザイン
研究デザイン
介入研究(PICO)
・ランダム化比較試験(RCT)
・クロスオーバー試験
・前後比較研究
観察研究(PECO)
・時間を考えない研究
・横断研究
・時間を考える研究
・コホート研究
・レトロスペクティブ研究(ケースコントロール研究、症例対照研究)
・その他
・症例報告
・症例集積研究
FINER
RQを洗練するフレームワーク
・F(Feasible):症例は集まるか?研究資金はあるか?協力してくれるスタッフはいるか?
・I(Interesting):医学的に興味深いか?世界の医療従事者の役に立ちそうか?
・N(Novel):未知か?
・E(Ethical):研究倫理に則っているか?
・R(Relevant):患者にとって切実か?(Interestingは医療従事者にとって有益、Relevantは患者にとって有益)
PICO/PECOとFINERの具体例
略
第4章 仮説検定
反証主義(統計学的仮説検定)
仮説が正しいことを証明する(立証)のは難しい
しかし、誤っていることを証明する(反証)のは簡単
(反証できる事例をひとつでも示せればよいため)
例えば、
「太陽は東から昇る」を証明したいとき、直接立証することは難しい
(1年間測定した結果は東から昇っていたとしても、翌日は西から昇るかもしれない)
そのため、統計学的仮説検定では、
まず「太陽は西から昇る」と仮説(帰無仮説)を立てて、
この仮説が確率的に起こりにくいことを示し、
帰無仮説を棄却することによって、
「太陽は東から昇る」(対立仮説)を主張する
統計学的仮説検定を行う場合に必要となる「確率的に起こりにくい」基準が、有意水準αである
「統計学的に有意差がある」ということと、「臨床的に意味がある」ということは全く関係がない
サンプルサイズを大きくすれば有意差は出せるので1万人集めれば治療薬Aに血圧を1mmHg下げる効果があると有意差を出せるかもしれないが、臨床的には1mmHg下がったところで意味がない
P値
・確率
・(本当は帰無仮説が正しいのに)誤って帰無仮説を棄却してしまう確率
信頼区間による補足
・P値のみでは情報が不足している(P値は有意差の有無しか示さない)ため、最近では信頼区間(推定の「不確かさ」の幅)を併記する場合が多い
※信頼区間は区間推定にも使われるが、仮設検定において信頼区間を使う場合は「推定の妥当性を評価するための情報」として使う(区間を推定するために使っているのではない)
信頼区間が、帰無仮説で設定した数値をまたいでいなければ、有意差がある
ここで、”帰無仮説で設定した数値”とありますが、例えば平均値の検定であるT検定。帰無仮説は「A群の平均値=B群の平均値」ですね。
つまりT検定での帰無仮説は、「A群の平均値ーB群の平均値=0」となります。
例えば、
・「A群とB群の平均値の差が10であり、その95%信頼区間が4~16だった」:有意差あり(0を跨いでいない)
・「A群とB群の平均値の差が5であり、その95%信頼区間が-2~12だった」:有意差なし(0を跨いでいる)

https://istat.co.jp/special/05/2
信頼区間の数学的な意味
・値の範囲:区間 [a, b]
・区間推定において、サンプリングを繰り返した場合、95%の頻度で、真の値(定数、母数など)が含まれる区間(真の値は、100回中95回は含まれるが、5回は含まれない)
・慣習的に、95%信頼区間(95%CI)を使う
・サンプルサイズが少ない場合、信頼区間は広くなる(狭められない)
▼実践編
実践編をはじめる前に
疑問をPICO/PECO形式に定式化できたら、解析方法を選定する
本書の課題は29個
第5章 Stataの概要
統計解析アプリを操作できれば何らかの出力は得られるが、統計解析を理解できていなければ出力が正しいか誤りかを判定できない
表計算アプリと統計解析アプリの違い
統計解析アプリの特徴
・データ登録には使えない:表計算アプリはデータ登録にも使える
・高度な統計解析ができる:表計算アプリでは基本的な統計解析しかできない
・解析のログが残る:表計算アプリでは残せない
統計解析アプリの例
・JMP
・R Commander:R言語実行用のGUI
・EZR
・SAS
・SPSS
・Stata
Stataのダウンロードとインストール
サンプルデータのダウンロード
Stataの基本操作
略
変数の種類
・アウトカム変数(従属変数、PECOにおけるO、結果とみなしたいもの):退院時ステータス(死亡/生存)、在院日数
・曝露変数(独立変数、PECOにおけるC、要因とみなしたいもの):新規治療Xの有無
・調整変数(独立変数、交絡因子になり得るもの):年齢、性別、など
課題(略)
課題1 変数一覧を確認する
課題2 データを閲覧する
第6章 検定方法の俯瞰
クロス集計表(分割表)の比較:母比率差の検定
・例:糖尿病有無と性別の割合、BMIカテゴリと性別の割合
・第9章を参照
2群間の比較:母平均差の検定、母中央値差の検定
・例:新薬有無とCRP(C反応性タンパク質)値
・第10章を参照
3群以上間の比較:母平均差の検定
・例:BMIカテゴリとTC(総コレステロール)値
・第11章を参照
連続変数間の比較:相関分析
・例:BMI値とTC値、身長と体重
・Pearson積率相関(パラメトリック)/Spearman順位相関(ノンパラメトリック)
多変量解析
・単変量解析:単一の変数について、特性を解析すること
・例:記述統計、分布の適合性検定(正規分布かどうか?)
・可視化:棒グラフ、ヒストグラム
・2変量解析:2つの変数(説明変数1個→目的変数1個)間の関係性を解析すること
・例:クロス集計表の比較、t検定、分散分析、相関分析、単回帰分析
・可視化:クロス集計表、散布図
・多変量解析:3つ以上の変数(説明変数N個→目的変数1個)間の関係性を解析すること
・例:重回帰分析/ロジスティック分析、主成分分析(PCA)、クラスタリング、判別分析、構造方程式モデリング(SEM)
・可視化:多次元散布図、クラスタマップ
生存時間分析
第14章を3章
第7章 データの可視化
・離散変数(二値変数、カテゴリ変数):度数分布表
・連続変数:ヒストグラム
度数分布表
・棒グラフで可視化できる
・各カテゴリが占める比率を算出できる
例:
・全患者における男女比
・全患者におけるBMIカテゴリ比
ヒストグラム
・連続変数をclassで区切り、class(階級)ごとのfrequency(データ件数)を算出してグラフ化したもの
・ヒストグラムと棒グラフは一見似ているが全く別物なので注意
例:
・全患者のCRP値の分布
※CRP値(C-Reactive Protein Score)[mg/dL]:C反応性タンパク質は、炎症や感染があると増加する(免疫反応として肝臓で産生される)
課題(略)
課題3 全患者の男女それぞれの割合を確認する(度数分布表)
課題4 全患者のBMIカテゴリごとの割合を確認する(度数分布表)
課題5 全患者のCRP値をグラフ(ヒストグラム)にして,全体像を確認する
課題6 全患者のCRP値をグラフ(箱ひげ図)にして,全体像を確認する
課題7 全患者の身長と体重の関係を確認する(散布図)
第8章 代表値の算出
・離散変数(二値変数、カテゴリ変数):割合
・連続変数
・正規分布の場合:平均値μ、標準偏差σ
※正規分布なので、平均値μや標準偏差σが意味を持つ
・非正規分布の場合:四分位範囲(中央値)
※正規分布ではないので、μ±σで表現できない
四分位範囲(IQR,interquartile range)
25パーセンタイル値と75パーセンタイル値を示す表現方式
・25パーセンタイル値(第1 quartile値):4個に区分けしたうち1個目の区切り
・50パーセンタイル値(第2 quartile値):中央値、4個に区分けしたうち2個目の区切り
・75パーセンタイル値(第3 quartile値):4個に区分けしたうち3個目の区切り
課題(略)
課題8 全患者の男女それぞれの代表値(割合)を確認する
課題9 全患者のBMIカテゴリごとの代表値(割合)を確認する
課題10 全患者のCRP値(正規分布)の代表値(平均・標準偏差)を確認する
課題11 全患者の在院日数(非正規分布)の代表値(中央値・四分位範囲)を確認する
第9章 2群間のカテゴリ変数の差(母比率差)
クロス集計表のどこかに偏り(偶然による誤差ではないズレ)があるか?
クロス集計表を眺めているだけでは結論は出せない
各セルの割合だけではなくサンプルサイズによってもP値は変わるため、必ず統計学的検定が必要になる
(クロス集計表なので、行列が転置されてもP値は不変)
群間の対応あり/対応なし
・対応あり:同一個体における介入前/介入後を比較する場合
・対応なし:別個体を比較する場合
検定方法の使い分け
・対応のない2群間
・Pearsonカイ2乗検定:P値の近似値を計算する、サンプルサイズが少ないと誤差が大きくなるため非推奨
・Fisher正確確率検定:P値を直接計算する(昔は計算資源が少なかったため実行しにくかった)、サンプルサイズが少ない場合でも正確に計算できる
・対応のある2群間:McNemar検定
課題(略)
課題12 新規治療Xと標準治療の男女の割合の差を検定する
参考:統計学的仮説検定の一般的なステップ
①帰無仮説と対立仮説を定義する
・母数を使って表現する
・例:帰無仮説H0「(母数)=定数」
②適切な検定方法を選定する
・検定したい仮説、データの種類、従う分布、サンプルサイズなどに基づき選定する
③検定方法に基づき、帰無仮説と観測値から検定統計量を算出する
・一般的に、検定統計量の絶対値が大きいと、それだけ稀な観測値であることを示している
・検定統計量の例
・z検定:z値(z分布に従う)
・t検定:t値(t分布に従う)
・カイ2乗検定:χ2値(χ2分布に従う)
・検定統計量(test statistics)を使わずにP値を算出する方法(正確検定 exact test)もある:二項検定、Fisher正確確率検定、など
コイン投げやくじ引きでは「ある事象が生じる確率」を実際に計算することができます。
そのため、計算した確率と有意水準を比較することで仮説の検定を行うことができます。
しかし、テストの点数、体重や薬の効果などを対象にする場合、データからその値が生じる確率を直接計算することはできません。
そのため、テストの点数は偏差値に、体重や薬の効果などのデータも、取りうる値の確率を計算するために確率密度分布に変換する必要があります。
検定統計量は、様々なデータを確率密度分布に変換することで、検定で利用しやすくした統計量です。
④検定統計量に対応するP値を算出する

https://hsugaku.com/29-20
・P値とは、「帰無仮説が正しいと仮定した場合に、観測値(またはそれ以上に稀な値)が観測される累積確率」
⑤P値を有意水準と比較して、帰無仮説の棄却可否を判定する
・一般的には、有意水準はα=5%
・検定統計量をP値に変換せずに、検定統計量のまま棄却域に入るかどうかで判定する方法もある(ただし、P値に変換した方が、検定の種類を問わず一律に扱えるようになるため便利)

限界値より右側の範囲が棄却域であり、検定統計量が棄却域に入っている(限界値≦検定統計量)ということは、即ち、P値≦有意水準αということを示している
https://corvus-window.com/whats_pvalue/
棄却の判断は、「P値(検定統計量をとりうる確率)」と「有意水準」の比較で判断します。
(検定統計量とP値は本質的には同じことを示している)
となると、棄却の判断には2つの考え方があります。
・検定統計量そのものから、有意水準と一致する検定統計量を比べる。
・検定統計量から一度P値に変換し、P値が有意水準以下かどうかを調べる。
検定統計量とP値は本質的には同じことを示しているので、どちらでもいいのです。ですが前者の方法には、短所があります。
それは、検定統計量は検定の種類(T検定やカイ二乗検定など)によって異なるため、検定について詳しく知っていないと大小関係の意味するものが変わるというものです。
そのため、一般的には検定統計量がらP値を計算し、有意水準と比較する方法がよく用いられます。どんな検定であれ、P値というものに変換さえすれば、あとは結果の見方が一律になります。
第10章 2群間の連続変数の差(母平均差・母中央値差)
パラメトリック検定/ノンパラメトリック検定
・パラメトリック検定:観測したデータが特定の分布(狭義には正規分布)に従うことを仮定できる場合の検定方法、数学的に扱いやすくなる
・ノンパラメトリック検定:観測したデータの従う分布が仮定できない場合の検定方法
適合度検定
パラメトリック検定を使う前に、特定の分布に従っていると見做せるかどうかを判定するための検定
正規分布に対する適合性
・Shapiro-Wilk検定:サンプルサイズが小さい場合に効果的
・Kolmogorov-Smirnoff検定
・Anderson-Darling検定:KS検定の改良版
・Jarque-Bera検定:サンプルサイズが大きい場合に効果的
他の分布に対する適合性
・カイ2乗適合度検定
・AIC/BICによる評価
実務的には、可視化して視覚的に判定することもある
・ヒストグラム
・QーQプロット(Quantile-Quantile Plot):分布が似ているかどうかを示す
検定方法の使い分け
・観測したデータが正規分布に従う場合
・対応のない2群間:対応のないt検定(Student検定)
・対応のある2群間:対応のあるt検定
・観測したデータが正規分布に従わない場合
・対応のない2群間:Wilcoxonの順位和検定、Mann-WhitneyのU検定
・対応のある2群間:Wilcoxonの符号付順位検定
※3群以上間の比較には使えないので注意
t検定:平均値の差を検定する
Wilcoxonの順位和検定、Mann-WhitneyのU検定:順位の総和の差を検定する
t検定
t値の定義式から解る通り、以下ほど大きな値になる
①平均値の差が大きい
②分散が小さい(データの信頼性が高い)
③サンプル数が多い(症例数が多い)
WMW検定(Wilcoxonの順位和検定、Mann-WhitneyのU検定)
観測データの値自体を使わず、順位のみ(順位を群ごとに合計した値)を使って検定する
課題(略)
課題13 新規治療Xと標準治療のCRP値の差を検定する(Studentのt検定)
課題14 新規治療Xと標準治療の在院日数の差を検定する(Wilcoxonの順位和検定)
第11章 3群以上の差(母平均差)
基本的に、3群以上の比較は解釈が複雑になるため非推奨(2群比較に分解する)
検定方法の使い分け
・観測したデータが正規分布に従う場合:分散分析(ANOVA)
・観測したデータが正規分布に従わない場合:Kruskal-Wallis検定
分散分析(ANOVA)
・分散分析しても、どの群間に差があるかは判らない(「どこかに差がある」ことしか判らない)
・どの群間に差があるかを判定するためには、多重比較検定を行う必要があるが、有意水準の補正などが複雑になる(Bonferroni補正、Holm法、Dunnett法、False Discovery Rate)
・1元配置ANOVA:因子は1つ(例:①土の種類、①薬の量)
・2元配置ANOVA:因子は2つ(例:①土の種類②肥料の量、①薬の種類②薬の量)
・多元配置ANOVA
Kruskal-Wallis検定
略
課題(略)
課題15 BMIカテゴリ(3群)で,総コレステロール値の差を検定する(ANOVA)
課題16 BMIカテゴリ(3群)で,在院日数の差を検定する(Kruskal-Wallis検定)
第12章 重回帰分析
多変量解析を行う理由
着目している因子だけでなく、他の因子も影響している可能性があるため
例:2群(標準治療 vs. 新規治療X)間のCRP値(連続変数)を検定した結果、「新規治療XではCRP値が高い」と有意差が出たとする。しかし、2群間には、もしかしたら性別や年齢などの別因子が影響しているのかもしれない
分析方法の使い分け
・アウトカムが連続変数:(回帰分析の結果表)/係数・信頼区間/重回帰分析
・アウトカムが二値変数:(回帰分析の結果表)/オッズ比・信頼区間/Logistic回帰分析
重回帰分析
目的変数に対する説明変数を選択する時のポイント
①相互に強く関連していそうな変数(多重共線性のある変数)を投入しない
・例えば、体重とBMIは両方とも臨床上重要な指標であるが、BMIは体重の関数(BMI=体重/身長^2)であるため、投入するならどちらか1個のみに限定する
②必要以上に多くの変数を投入しない
・一般論として、目的変数の数は、(サンプル数÷15)個以下に留める
・変数が多いほどオーバーフィッティングを起こしやすくなる
課題(略)
課題17 重回帰分析で調整変数を調整した新規治療Xと在院日数の関連を調べる
第13章 Logistic回帰分析
重回帰分析の場合と同様に配慮して、投入する説明変数を選定する
目的変数の上限数
ロジスティック回帰分析の目的変数の上限数は、
・アウトカム発生数≦全体の50%:(アウトカム発生数÷10)
・全体の50%<アウトカム発生数:(アウトカム非発生数÷10)
つまり、
・症例数が1,000ケース(うち死亡が137ケース)の場合:137/10=13.7で13個まで目的変数を投入できる
・症例数が1,000ケース(うち死亡が600ケース)の場合:400/10=40で40個まで目的変数を投入できる
オッズ比
・ロジスティック回帰分析の結果を解釈する上で、オッズ比で算出する
ロジスティック回帰分析は、モデル式によって説明変数から目的変数を予測するだけではなく、説明変数が目的変数にどの程度影響を与えているのかも、明らかにします。その指標が、オッズとオッズ比です。
オッズ比は「1」に近いほど、二つのグループでの発病のしやすさが同程度ということになります。
回帰係数:説明変数の各変数が1変化したときの目的変数の変化量
Z値(t値):回帰係数を標準誤差(*1)で割った値
p値:変数が目的変数に対して影響があるかを測るための値
オッズ比:ある説明変数が最終的な結果にどれだけ影響を与えているのかの指標
・リスク比が3の場合は、「喫煙者は、非喫煙者に比べて、肺がんを発症するリスクが3倍である」と解釈できる
・オッズ比が3の場合は、「喫煙者は、非喫煙者に比べて、肺がんの発症しやすさが3倍である」とは解釈できない
なぜ解釈しにくいオッズ比が使われているのか?
・ロジスティック回帰分析との相性が良い:医療統計ではロジスティック回帰分析を多用するため、結果的にオッズ比も多用される
・コホート研究でもケースコントロール研究でも使える:コホート研究ではリスク比もオッズ比も使えるが、ケースコントロール研究ではリスク比が使えない
・イベント発生確率pが小さければ、オッズ比はリスク比の近似になっている
課題(略)
課題18 Logistic回帰分析で新規治療Xと在院死亡の関連を調べる
第14章 生存時間分析
生存時間分析の分類
単変量解析として
・目的:生存時間の分布を解析し、イベントの発生パターンを把握する
・手法:Kaplan-Meier曲線(累積生存率曲線)、log-rank検定、ハザード比
・例:機械の故障時間、新規治療を受けた患者の生存時間
多変量解析として
・目的:生存時間と他因子の関係を解析し、生存時間に影響を与える因子を把握する
・手法:Cox回帰
Cox比例ハザードモデル、ハザード比、Cox回帰、パラメトリック生存モデル
・例:材料変更が機械の故障時間に与える影響、新規治療が生存時間に与える影響
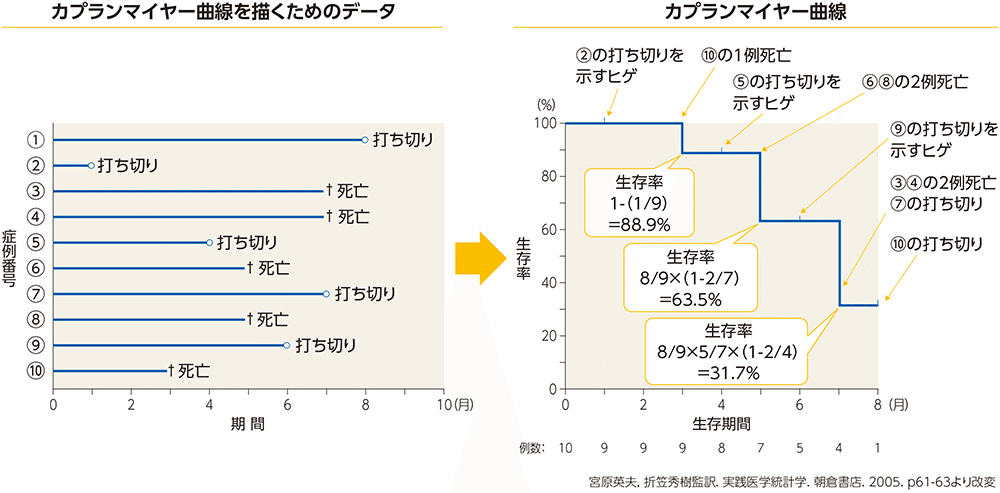
Kaplan-Meier曲線(累積生存率曲線)
生存時間データの分布を可視化する方法
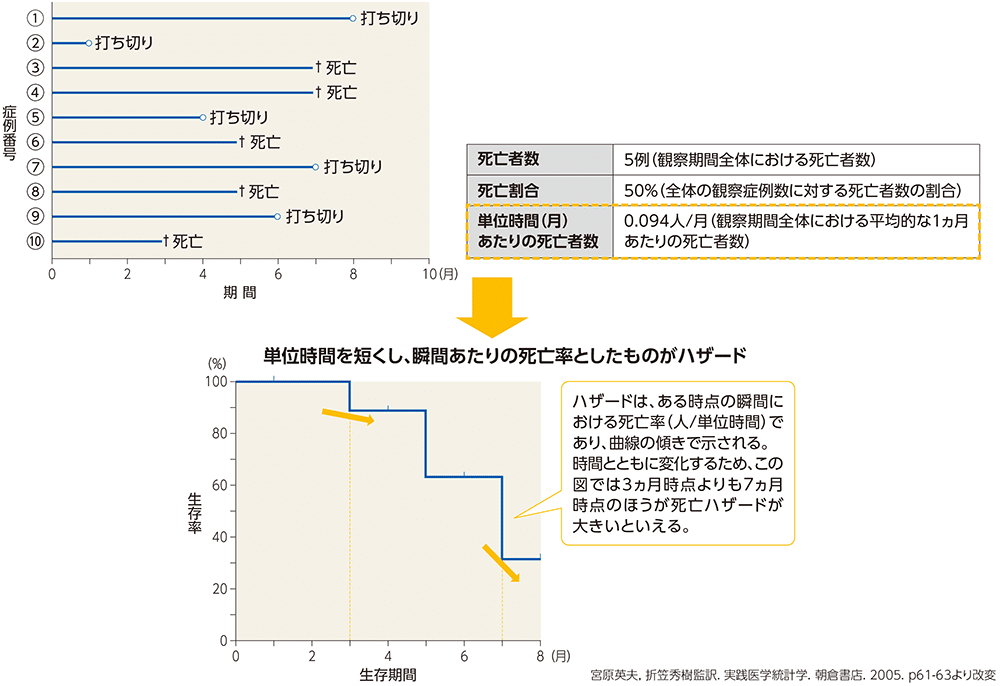
ハザード
・イベントが発生する速度(単位時間あたりイベント発生率)
・算出式:イベント発生数÷延べ観察期間
※延べ観察期間[人年]:何人を何年間観察したか
例:6個体を5年間追跡し、死亡イベントの発生を観察した
個体A:5年間生存
個体B:2年目末に死亡
個体C:4年目末に死亡
個体D:3年目末に死亡
個体E:4年目で打ち切り
個体F:1年目末に死亡
この場合、
・イベント発生数:4[件](最終的に4人が死亡したため)
・延べ観察期間:5+2+4+3+4+1[人年]
つまり、
ハザード=4/19=0.21[人年]
(「100人を1年間追跡すると、21人が死亡する」と解釈できる)
ハザード比(HR, Hazard Ratio)
・算出式:(介入群のハザード)÷(コントロール群のハザード)
・ハザード比が1であれば群間差なし、1から遠ければ群間差あり
・ハザード比は介入の効果を示すわけではないことに注意

介入の効果
・算出式:(コントロール群の生存割合)^(ハザード比) ー (コントロール群の生存割合)
例:
・コントロール群の5年生存率:79.2%
・ハザード比:0.65
の場合、治療の効果は、(0.792)^(0.65)-(0.792)=0.0674
つまり6.7%生存率を上げたことになる
log-rank 検定・一般化Wilcoxon検定
2群間の生存曲線に差があるかどうかの検定
特定時点の生存率ではなく、生存曲線全体を比較できる
ログランク検定と一般化ウィルコクソン検定の使い分け
・「時間がたてばたつほど、群間差が開いてくる」タイプのデータに対しては、一般化ウィルコクソン検定よりもログランク検定の方が、有意差がつきやすくなる。
・一方、「結局ほぼ全員が死亡するのだけど、生存時間が延びる」タイプのデータでは、一般化ウィルコクソン検定の方が、差がつきやすくなる。
Cox回帰分析
・様々な因子(説明変数)が生存時間(説明変数)に与える影響を評価する方法
・Cox回帰分析は、2群の生存曲線が「どの時点でもハザード比は一定(比例ハザード性)」という仮定(Cox比例ハザードモデル)に従うことを前提としている
※Cox比例ハザードモデルに従っているかどうかは、Schoenfeld残差などより検証可能
・投入可能な説明変数の量は、ロジスティック回帰分析と同じ考え方
「Cox比例ハザードモデル=生存時間解析での多変量解析」というイメージでOK
・アウトカムが連続変数の時:重回帰分析(共分散分析)
・アウトカムがカテゴリカル変数の時:ロジスティック回帰分析
・アウトカムが生存時間データの時:Cox回帰分析
課題(略)
課題19 生存時間分析で新規治療Xと90日死亡の関連を調べる
結果を表にまとめる
略
第15章 データクリーニングの基礎
臨床研究の解析結果は、再現性を担保する必要があるため、実行したコマンドも、コマンドによる処理結果と共に保存しておく必要がある
課題(略)
課題20 CSVファイルを読み込む
課題21 性別,身長,体重の変数を文字列から数値に変更する
課題22 性別の変数を数値から文字列に変更する
課題23 性別の変数を使って,femaleという新しい変数を作成する
課題24 身長「height」と体重「weight」からbmi2という新しい変数を作成する
課題25 生年月日の文字列変数「dtbirthstr」から数値の変数「birthday」を新しく作成する
課題26 変数「bmi2」を削除する
課題27 同一行の複数の変数のなかで最大値を特定し,その値を新たな変数とする結果を記録する
課題28 解析結果を記録する
課題29 コマンドを保存する
第16章 Stataを使いこなすために
公式Youtube
日本の販売代理店
おわりに
やさしい臨床研究セミナー公式アカウント
コラム
◆コラム1 統計学に名を遺した人たち
ピアソン(1857-1936)
・英ケンブリッジ大
・区間推定や仮説検定を理論化
・χ二乗検定、ヒストグラム
フィッシャー(1890-1962)
・英ケンブリッジ大
・ロザムステッド農業実験場
・正確確率検定、分散分析、最尤法
・愛煙家、相関関係と因果関係は違う
ゴセット(1876-1937)
・英オックスフォード大
・ギネス醸造所、ペンネームStudent
・t検定
コックス(1924-)
・英ケンブリッジ大
・ロジスティック回帰分析、Cox回帰分析
◆コラム2 相関分析で見ているものとは
・正規分布同士の相関関係:Pearson相関係数
・どちらか一方が非正規分布である相関関係:Spearman順位相関係数
相関関係があるからといって、因果関係があるとは限らない
データセットから得られた相関係数が有意ではない(偶然得られたものである)可能性もあるため、P値をチェックする必要あり
◆コラム3 奇跡の確率
略
◆コラム4 簡単にクロス集計表の検定をしたいとき
略
◆コラム5 カイ二乗検定とFisherの正確確率検定の計算法
略
◆コラム6 対応のない?対応のある?
略
◆コラム7 分散とは?〜データのバラつきをイメージする
略
◆コラム8 回帰分析における基準の変更と表示
略
◆コラム9 論文や学会発表で記載すべき桁数
臨床的に意味がある桁数で記載する(細か過ぎても意味ない)
必要に応じて1桁多く記載する
例えば、有意水準0.05と比較するために、P値は0.049や0.051の桁まで記載すべき
パーセンテージを記載する場合は、分子と分母の値も併記する
(同じ33%でも、1/3と1000/3000では意義が異なるため)
◆コラム10 データの保存形式と文字コード
互換性を高めるため、文字符号化方式(エンコーディングスキーム)はUTF-8にして、CSV形式のテキストファイルに保存することが原則
