
ピタゴラスと√2の戦い
万物は数である (哲学の時代)
「万物は数である」
BC6世紀にそういったのは数学者であり哲学者でもあったピタゴラスです
ここでいう『数』とは自然数とその比のことです
その頃ギリシャの色々なところで様々な哲学が生まれていました
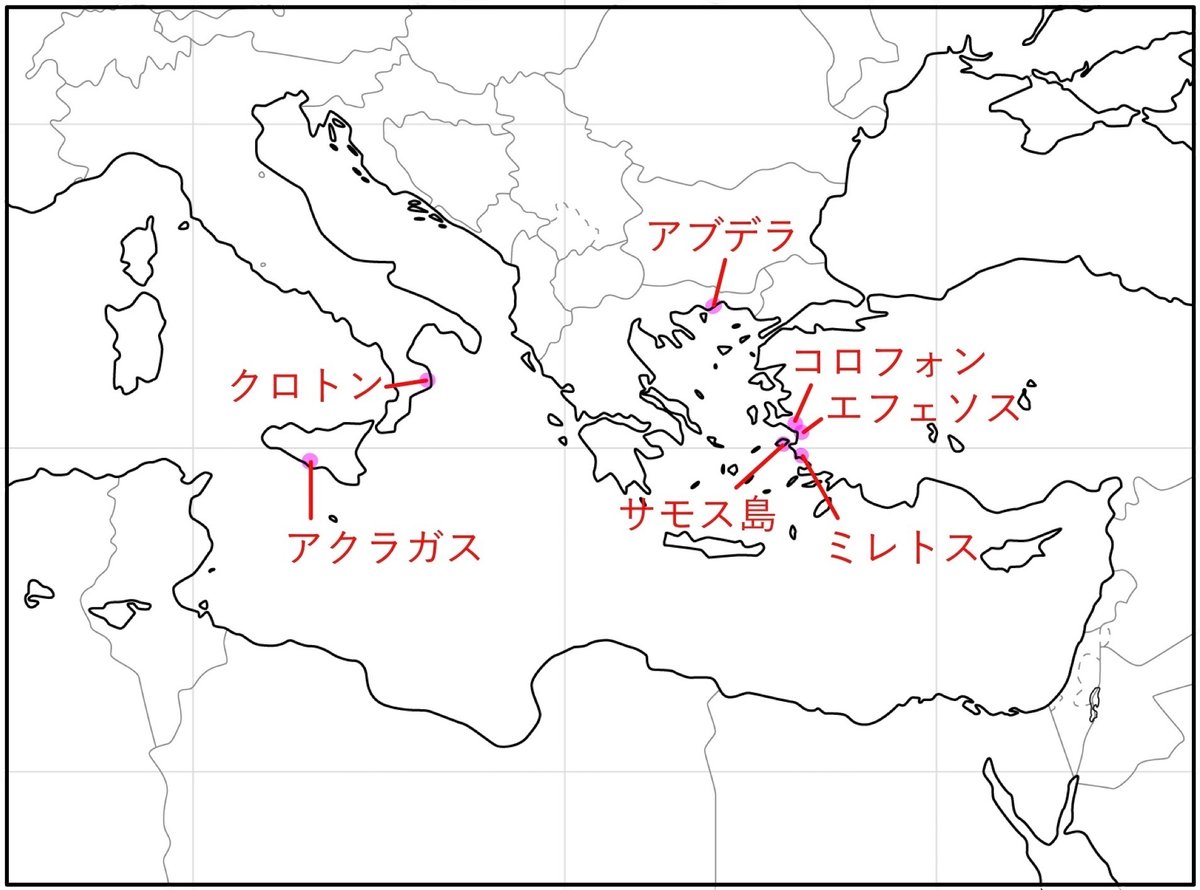
例えば
ミトレスにいたタレスは『水』、
同じくミトレスにいたアナクシメネスは『空気』、
トラキア地方のアブデラにいたデモクリトスは『アトム(原子)』、
エフェソスにいたヘラクレイトスは『火』、
コロフォンにいたクセノパネスは『土』、
シチリア島のアクラガスにいたエンペドクレスはそれらを合わせた
『四元素(火、水、土、空気)』
と考えてました
ピタゴラスも数学者であり哲学者でもあったので、『数』以外にも色々なことを考えていたようです
例えば地球は円盤ではなく球であるとか……
ピタゴラス教団の設立
ピタゴラスはBC582サモス島で生まれました
ピタゴラスが『サモスの賢人』と言われるのはそのためです
彼は30歳頃旅に出ます
エジプトやバビロニアを回り見聞を広げたようです
当時のエジプトやバビロニアは数学が盛んでしたからピタゴラスも大いに影響を受けたのだと思います
20年ほど旅をしたピタゴラスは50歳の頃、故郷サモス島に帰ってきましたが、その地は暴君によって支配されていました
そこで彼はクロトンという町に逃れ、そこで学校を作ることにしました
『ピタゴラス教団』の始まりです
ピタゴラス派の根本思想は均整及び調和の理念です
ピタゴラス教団には厳しい戒律もありましたが、色々な成果もありました
ピタゴラス音階
その1つはピタゴラス音階です
ある日散歩をしていると鍛冶屋がハンマーで叩く音が聞こえてきました
よく聞くときれいに響き合う音と、そうでない音と違いがあることに気がつきました
戻って調べてみると
元の弦の音が『ド』とすると
弦の長さが半分になると、1オクターブ高い『ド』の音が鳴り
弦の長さが $${\displaystyle \frac{2}{3}}$$ だと(元の弦の長さとの比が $${3:2}$$ だとすると)『ソ』の音が鳴り
弦の長さが $${\displaystyle \frac{3}{4}}$$ だと『ファ』の音が鳴りますが
これらの音がきれいに響き合う音であることが分かりました
残った『レ』『ミ』『ラ』『シ』もほかの音と弦の長さの比が $${3:2}$$ または $${4:3}$$ であれば響き合うと考えて
『レ』:『ソ』$${\! \!=4:3}$$ 、『レ』:『ラ』$${\!\!=3:2}$$ 、『ミ』:『ラ』$${\!\!=4:3}$$ 、
『ミ』:『シ』$${\!\!=3:2}$$
としました
そうしてできたのがピタゴラス音階です
ここでは低い音の『ド』の音の弦の長さを1としてまとめておきます
$${\begin{matrix}ド & レ & ミ & ファ & ソ & ラ & シ & ド \\1 & \frac{8}{9} & \frac{64}{81} & \frac{3}{4} & \frac{2}{3} & \frac{16}{27} & \frac{128}{243} & \frac{1}{2} \end{matrix}}$$
またこれを元にして工夫されたのが純正律(バルトロメ・ラモス 1482)や平均律(メルセンヌ 1636)です
楽曲も作られた時代によって調律が変わるのも面白いかもしれません
ピタゴラスの定理
この事実はバビロニアやエジプトでは知られていたようです


一般化したのがピタゴラスです
$${a^2+b^2=c^2}$$
美しい定理ですし、
$${(a,\ b,\ c)=(3,\ 4,\ 5),\ (5,\ 12,\ 13),\ (8,\ 15,\ 17),\ \cdots}$$
といくらでも求めることができます
この数の組をピタゴラス数と呼びます
エジプトでは
エジプトでは縄師と呼ばれる人たちがいました
毎年起こる「ナイルの恵み」と呼ばれる大洪水のあと、もう一度土地の区画整理を行わなければならなかったからです
そこで使われたのが、1つの輪を12等分されたもの
3、4、5のところで縄を張ると直角三角形が出来上がります
こうやって区画の分からなくなった土地を正確に分けていったということです

エジプトやバビロニアを旅したピタゴラスはこういった知識も得ていたと思われます
√2の衝撃
そうして得られたピタゴラスの定理
しかし神はあまり優しくありませんでした
ある日弟子のヒッパソスは $${\sqrt{2}}$$ を発見してしまったのです
残念ながらこの数は自然数でもその比(有理数のこと)でもありませんでした
ピタゴラスはヒッパソスのこのことを漏らしてはいけないと厳命しました
もともとピタゴラス教団は秘密主義で得られた成果も公開されることはありませんでしたが、今回のことは教団の存在意義を揺らがす非常に危険なものだったからです
しかし、ヒッパソスはこのことを他人に話してしまい、溺死の刑にされてしまったということです
★√2が無理数という証明 (嫌いな人はサラッと)
ピタゴラスがした $${\sqrt{2}}$$ が無理数であるという証明はいくつか説がありますが、そのほとんどが背理法という方法を用いて証明されています
背理法とは
背理法とは
AであるならばBである
という主張に対して
『Bでない』と仮定して、Aであるという条件と合わせて議論していくと、矛盾が生じるという
だから、はじめの『Bでない』は間違いで『Bである』が正しいという説明方法です
例 直線 $${\ell}$$ とその直線の外にある点Pがある
点Pから直線 $${\ell}$$ には垂線は1本しか引けないことを証明せよ

普通は図1が当たり前、以上終了ですが、証明は当たり前をもう少し正確に説明する必要があるのです
証明 図2のように
もう1本垂線PBが引けたとする (『Bでない』とするの部分)
そうすると△PABができるが、
内角の和が180°より大きくなって
「三角形の内角の和は180°」という主張に反する (矛盾の発生)
よって2本引けるという主張が間違いで、垂線は1本しか引けない
高校ではこういう簡単な例を挙げてくれなくて(あくまでも式を使った証明の単元だから)みんな嫌になっちゃうんですよ
まあ、ピタゴラスは偉大ですからあの教科書の証明をやっていたともいわれています。
それでは、ピタゴラスがしたのではないかという証明をいくつか……
(できるだけ簡単なものから)
「√2が無理数である」の証明
証明1 $${\displaystyle \sqrt{2}=\frac{m}{n}}$$ とする (『Bでない』とするの部分)
このとき$${\displaystyle 2=\frac{m^2}{n^2}}$$
$${m^2=2n^2}$$
両辺を素因数分解すると
左辺は素因数2が偶数個、右辺は2倍しているから奇数個となって矛盾
よって $${\sqrt{2}}$$ は $${\displaystyle \frac{m}{n}}$$ の形で表すことができない
(=無理数である)
証明2

直角二等辺三角形ABCがあり、
点Cを中心に半径BCの円を描きACとの交点をDとする
DからACに対して垂線を描き、ABとの交点をEとする
この直角二等辺三角形ABCは
辺の長さを自然数で描くことができる最小のものとする
今BC、AC(=AB)は自然数すると (『Bでない』とするの部分)
ある数 $${a}$$ を使って何倍かの形で表すことができる
BC=DC だから AD=AC-DC である AD も
ある数 $${a}$$ を使って何倍かの形で表すことができる ……①
また△ADEは∠A=45°、∠D=90°だから∠E=45°の直角二等辺三角形
よってAD=ED
線分EBとEDはともにおうぎ形CBDの接線であるからEB=ED
ゆえにAD=ED=EB
①よりEBもある数 $${a}$$ を使って何倍かの形で表すことができる……②
AE=AB-EB だから
AEもある数 $${a}$$ を使って何倍かの形で表すことができる ……③
①②③より△ADEは辺の長さが
ある数 $${a}$$ を使って何倍かの形で表すことができて、
かつ元の△ABCより小さな直角二等辺三角形になることが分かった
これは最小の自然数の長さの直角二等辺三角形を描いた
ということに矛盾する
よって $${\sqrt{2}}$$ は有理数にはならない
が、しかし!
ピタゴラスは教団をつくってまで色々なことを考えてきました
彼が望んだものは、教団の存在意義を否定する証明だったのでしょうか
そのあたりを次回その2で考えてみたいと思います
