
自己相似図形の世界
シェルピンスキーのギャスケット

正三角形の中から半分の大きさの正三角形を切り出し、さらに残った3つの正三角形からその半分の大きさの正三角形を切り出します
こうして残った図形の正三角形部分から半分の大きさの正三角形を切り出す作業を続けるとどうなるでしょう
どの一部分を見ても全体と相似に見えませんか
このような図形のことをフラクタルといいます
先ほど取り上げた図形は『シェルピンスキーのギャスケット』といいます
この極限図形の面積は0です
なぜかというと、元の正三角形(図1)の面積を1とすると、図2の1つ切り出した図形の面積は $${\displaystyle\frac{3}{4}}$$ の大きさになり、
図3の図形の面積はさらに $${\displaystyle\frac{3}{4}}$$ の大きさになり $${\displaystyle\left(\frac{3}{4}\right)^2}$$、
図4の図形の面積はさらに $${\displaystyle\frac{3}{4}}$$ の大きさになり $${\displaystyle\left(\frac{3}{4}\right)^3}$$、
図5の図形の面積は $${\displaystyle\left(\frac{3}{4}\right)^4}$$……
極限図形の図∞のシェルピンスキーのギャスケットの面積は $${\displaystyle \lim_{n \to \infty}\left(\frac{3}{4}\right)^{n-1}=0}$$
さて、面積が0だからといって次元も0ということ訳ではありません
少なくとも線より太そうなもので構成されているであろう図形ですから1次元以上2次元未満といったところでしょうか
一般的に、2次元の図形は相似比が $${1:2:3}$$ であれば、面積比は $${1^2:2^2:3^2}$$ となり
3次元の図形は相似比が $${1:2:3}$$ であれば、体積比は $${1^3:2^3:3^3}$$ となります

どうやら比の「指数部分」が次元を表しているようです
では、シェルピンスキーのギャスケットはどうでしょう

赤丸の部分を1とみて2倍の図形(もとの図)にするには3つ同じものが必要になりますね
つまり相似比 $${1:2}$$ に対して、面積比は $${1:3}$$ ということになります
したがってフラクタル次元を $${n}$$ とすると $${2^n=3}$$ が成り立つことになり、
シェルピンスキーのギャスケットは $${n=\log_2 3=1.5849\cdots}$$ 次元ということになります
わぁ、非整数の次元が出てきましたよ
シェルピンスキーのギャスケットの3D版

今度はシェルピンスキーのギャスケットの3D版を考えてみましょう
作り方は元の正四面体(図1)から外側の4つの $${\displaystyle \frac{1}{2}}$$ の正四面体を残してごっそり抜き取ります
元の正四面体の体積を1とすると図2の立体の体積は $${\displaystyle\frac{1}{8}}$$ の体積をもつ正四面体が4つあるわけですから $${\displaystyle\frac{1}{8}\times 4=\frac{1}{2}}$$ になります
図3の立体の体積は図2のさらに $${\displaystyle\frac{1}{2}}$$ で $${\displaystyle\frac{1}{4}}$$ 、図4は $${\displaystyle\frac{1}{8}}$$ 、図5は $${\displaystyle\frac{1}{16}}$$ 、
図∞だと $${\displaystyle\lim_{n \to \infty}\left(\frac{1}{2}\right)^{n-1}=0}$$ となります
では次元はどうでしょう
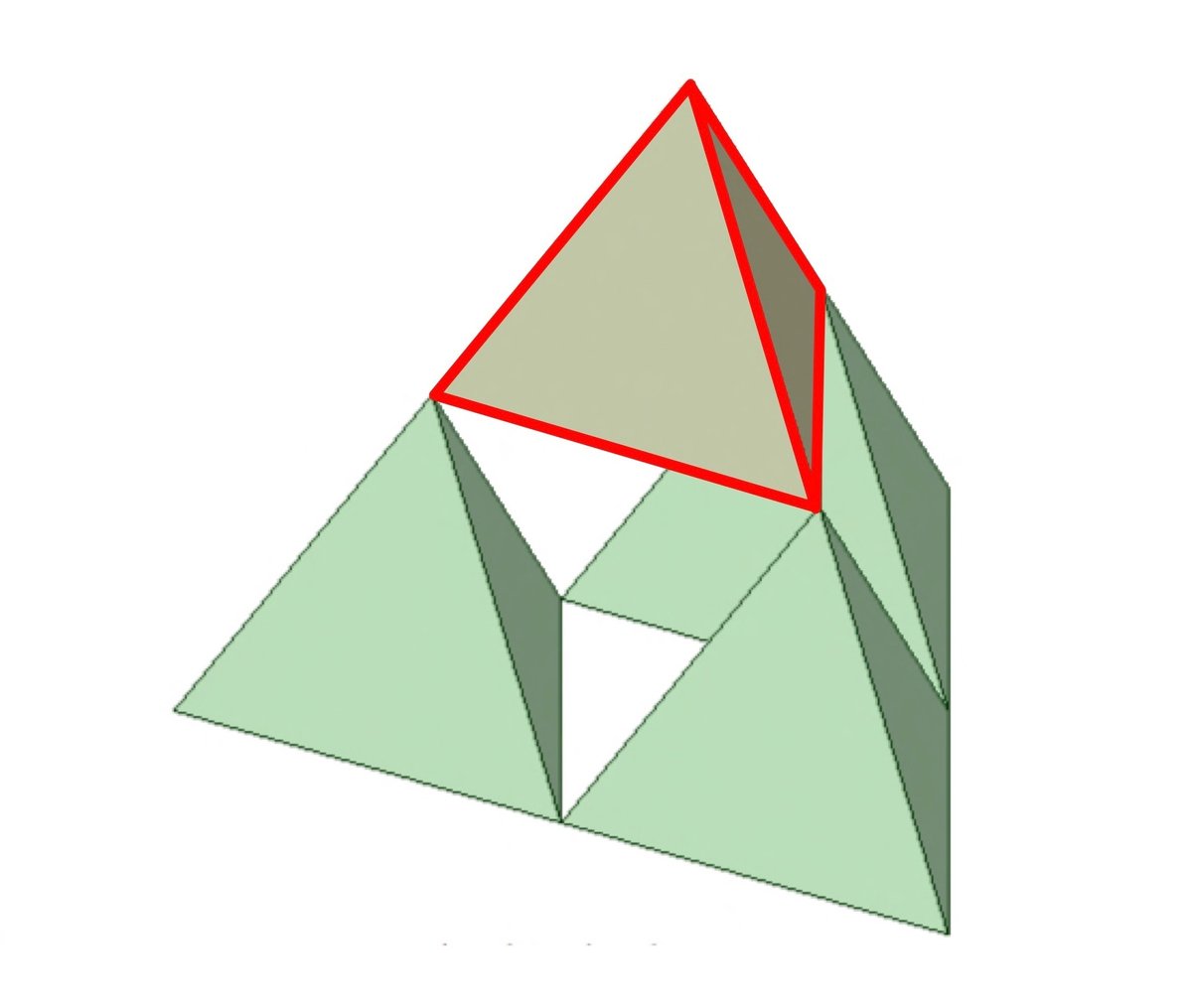
赤の部分を1とみて2倍の図形(もとの図)にするには4つ同じものが必要になりますね
つまり相似比 $${1:2}$$ に対して、体積比は $${1:4}$$ ということになります
したがってフラクタル次元を $${n}$$ とすると $${2^n=4}$$ が成り立つことになり、シェルピンスキーのガスケットの3D版は $${n=2}$$ 次元ということになります!
これ凄くないですか?
非整数次元も驚きでしたが、がんばってつくった立体の次元が2次元ですよ
次元というものがどんなものと考えたらいいか混乱しそうになりますね
カントール集合

カントール集合という不思議な線分(?)について考えてみましょう
図1では線分があり長さ1としましょう
図2ではその線分のうち真ん中 $${\displaystyle\frac{1}{3}}$$ だけ抜いた図形を考えます
元の線分も残してあります
図3ではさらに残った2本の線分について、その線分のうち真ん中 $${\displaystyle\frac{1}{3}}$$ だけ抜いた図形を考えます
図4も同じように残った4本の線分について作業します
こうして無限に繰り返したものがカントール集合です
線分の長さの合計は1回作業をするごとに作業する前の $${\displaystyle\frac{2}{3}}$$ の量になりますからカントール集合の線分の長さは $${\displaystyle\lim_{n\to \infty}\left(\frac{2}{3}\right)^{n-1}=0}$$
ちなみに線分の数は、図1で1本、図2で2本、図3で4本と1回作業をするごとに2倍になります
よって $${\displaystyle\lim_{n\to\infty} 2^{n-1}=\infty}$$
さて極限的に長さ0の図形が、その構成しているものの数としては無限大であるとはいかなる状態なのでしょうか
さて次元を考えるとき、今までと逆の発想をしてみます

青の正四面体の $${\displaystyle \frac{1}{2}}$$ は赤の正四面体で(相似比 $${1:2}$$ )、右の図を赤の正四面体で構成するには4倍必要と考えて、フラクタル次元を $${n}$$ とすると
$${2^n=4}$$
という式が得られる
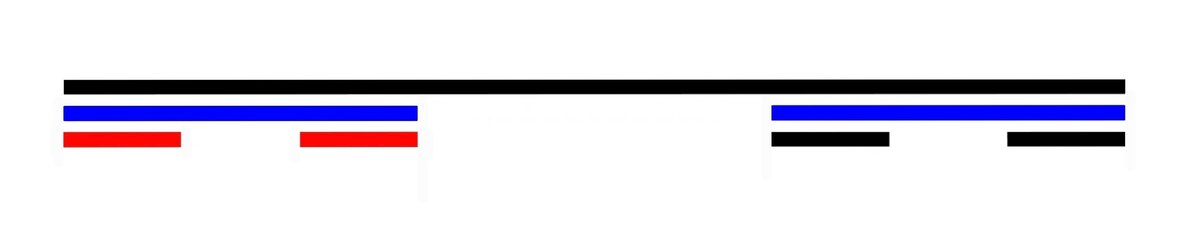
同じように考えて、
2段目の青の線分の $${\displaystyle\frac{1}{3}}$$ が赤の線分である(相似比 $${1:3}$$ )とすると、3段目を構成するには2倍必要なので、フラクタル次元を $${n}$$ とすると
$${3^n=2}$$
$${\therefore n=\log_3 2=0.6309\cdots}$$
やはり普通の線分よりかはフラクタル次元は低かったようです
でも、点(0次元)を無限個集めたものだからカントール集合も0次元かと思ってました
絶妙なバランスが存在していたのですね
コッホ曲線

正三角形の三辺でつくると雪の結晶のような図形ができるものです

作り方は線分を3等分して真ん中を消し、その代わりに正三角形の残りの2辺を描くという作業を繰り返していくものです
この作業でできる折れ線は特徴的なことがあります
1つは図1の線分の長さを1とすると、図2は $${\displaystyle\frac{4}{3}}$$ になりますね
1回作業を行うと $${\displaystyle\frac{4}{3}}$$ 倍になるので、図3は $${\displaystyle\left(\frac{4}{3}\right)^2}$$ になります
同じように考えて、図4は $${\displaystyle\left(\frac{4}{3}\right)^3}$$、図5は $${\displaystyle\left(\frac{4}{3}\right)^4}$$、図6は $${\displaystyle\left(\frac{4}{3}\right)^5}$$ となり、
極限図形の図∞は $${\displaystyle\lim_{n \to \infty} \left(\frac{4}{3}\right)^{n-1}=\infty}$$ つまりこの作業を繰り返していくと長さが無限大になってしまうのです
もう1つ

図1の横線をずーっと引き続けるとすると、閉じた図形ができ面積が求まります
図2′の正三角形の面積を $${a}$$ とすると、図3′ではそれに加えて $${\displaystyle\frac{1}{9}}$$ の大きさの正三角形が4個できます
図4′ではさらにその $${\displaystyle\frac{1}{9}}$$ の大きさの正三角形が $${4^2}$$ 個できます
まとめると、面積は
図2′では $${a}$$
図3′では $${\displaystyle\left(1+\frac{1}{9}\times 4\right)a=\left(1+\frac{4}{9}\right)a}$$
図4′では $${\displaystyle\left\{1+\frac{1}{9}\times 4+\left(\frac{1}{9}\right)^2\times 4^2\right\}a=\left\{1+\frac{4}{9}+\left(\frac{4}{9}\right)^2\right\}a}$$
よって図∞′を作ったとすると、$${\displaystyle\left\{1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+\left(\frac{4}{9}\right)^3+\left(\frac{4}{9}\right)^4+\cdots\right\}a}$$
この無限等比級数は公比 $${\displaystyle r=\frac{4}{9}}$$ が $${-1 < r < 1}$$ より収束し、
その和は $${\displaystyle\frac{1}{\displaystyle 1- \frac{4}{9}}a=\frac{9}{5}a}$$ となります
無限の周の長さをもつ図形の面積が有限というのはかなり変わっていると思いませんか
さてこの曲線ですが、折れ線を増やしていっただけなので、次元は1のはずです

でもカントール集合のように考えてみると、赤の図形は青の図形の $${\displaystyle \frac{1}{3}}$$ で赤の図形ですべてを構成するには4つ必要なので、フラクタル次元を $${n}$$ とすると
$${3^n=4}$$
$${\therefore n=\log_3 4=1.2618\cdots}$$
無限の長さをもつ曲線は次元も一筋縄ではいかないようです
メンガーのスポンジ

メンガーのスポンジとは立方体(図1)からその相似比 $${\displaystyle \frac{1}{3}}$$ の大きさの立方体を各面の中央から中心部分も含めて7個を取り除いたもの(図2)です
図3は残った20個の立方体について同じことを行ったものです
図4は残った $${20^2=400}$$ 個の立方体について同じことを行ったものです
元の立方体(図1)の体積を1とすると、図2の立体の体積は $${\displaystyle \frac{20}{27}}$$ 、図3の立体の体積は$${\displaystyle \left(\frac{20}{27}\right)^2}$$ 、図4の立体の体積は$${\displaystyle \left(\frac{20}{27}\right)^3}$$ 、
図∞の立体が作れたとすると、その体積は$${\displaystyle \lim_{n \to \infty} \left(\frac{20}{27}\right)^{n-1}=0}$$

さてフラクタル次元ですが、赤の立方体は青の立方体の $${\displaystyle\frac{1}{3}}$$ で、右の図を赤の立方体で構成するには20個必要になります
よって、フラクタル次元 $${n}$$ は
$${3^n=20}$$
$${\therefore n=\log_3 20=2.7268\cdots}$$
まとめ
色々なフラクタルについて見てきました
極限図形では面積や体積が0なのに、フラクタル次元という新しい次元の考え方を導入すると、非整数の次元が得られたり、立体なのに2次元だったり、また、曲線の長さが0なのに次元が0より大きかったり、長さが無限大の曲線だと次元も1を越えていたり……
フラクタルの図形はまだまだたくさんありますし、色々な興味深い性質を持っています
実用化されているものもあるので色々な探してみてください
次の写真はシェルピンスキーのギャスケット3D版を実用化した例です

引用元:『京都大学 吉田キャンパス Newシェルピンスキーの森』
http://www.gaia.h.kyoto-u.ac.jp/~fractal/detail/7a.html
