ものの見方を変えてみれば……

双対の原理

数学の定理や問題の中には一見すると違ったものが見方を変えると似ているものがあります
例えば高校1年で習うチェバの定理とメネラウスの定理があげられます

この2つの定理ではどちらも条件を満たせば
　$${\displaystyle \mathrm{\frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR}{RB}}=1}$$
という式が成り立ちます
全く違った条件の図で同じ等式が導かれるのは不思議と思ったことはありませんか
実は『双対』の原理を使うとこの2つの図は同じように見えてくるのです
『双対』の原理とは
　「点」と「直線」、「…の上にある」と「…を通る」、
　「共線」と「共点」$${{}^※}$$、「交わり」と「結び」をいっせいに
　互いに入れ替えたとき、結果として得られる命題は定理として成り立つ
　というものです
　　※共線……3直線が共通、つまり3点が一直線上にある
　　　共点……3つの交点が共通、つまり3直線が1点で交わる

こういった双対の考え方は幾何学だけでなく、論理学や電気と磁気の間、ほかにも色々な分野で現れます


さて、ものの見方を変える（立場を変える）問題は色々あります

極と極線に関する問題

問題　円 $${x^2+y^2=16}$$ と点A$${(7,\ 5)}$$ がある
　　　Aから円に接戦を2本引きその接点をP, Qとする
　　　(1) 直線PQの方程式を求めよ
　　　(2) PQ上にあって円外の点をBとする
　　　　　Bから円に接戦を2本引きその接点をS, Tとする
　　　　　直線STは点Aを通ることを示せ

　(1)で点Aを極、直線PQをそれに対する極線といます

（解答を折りたためないので5行ほど空白を空けています）

解(1)

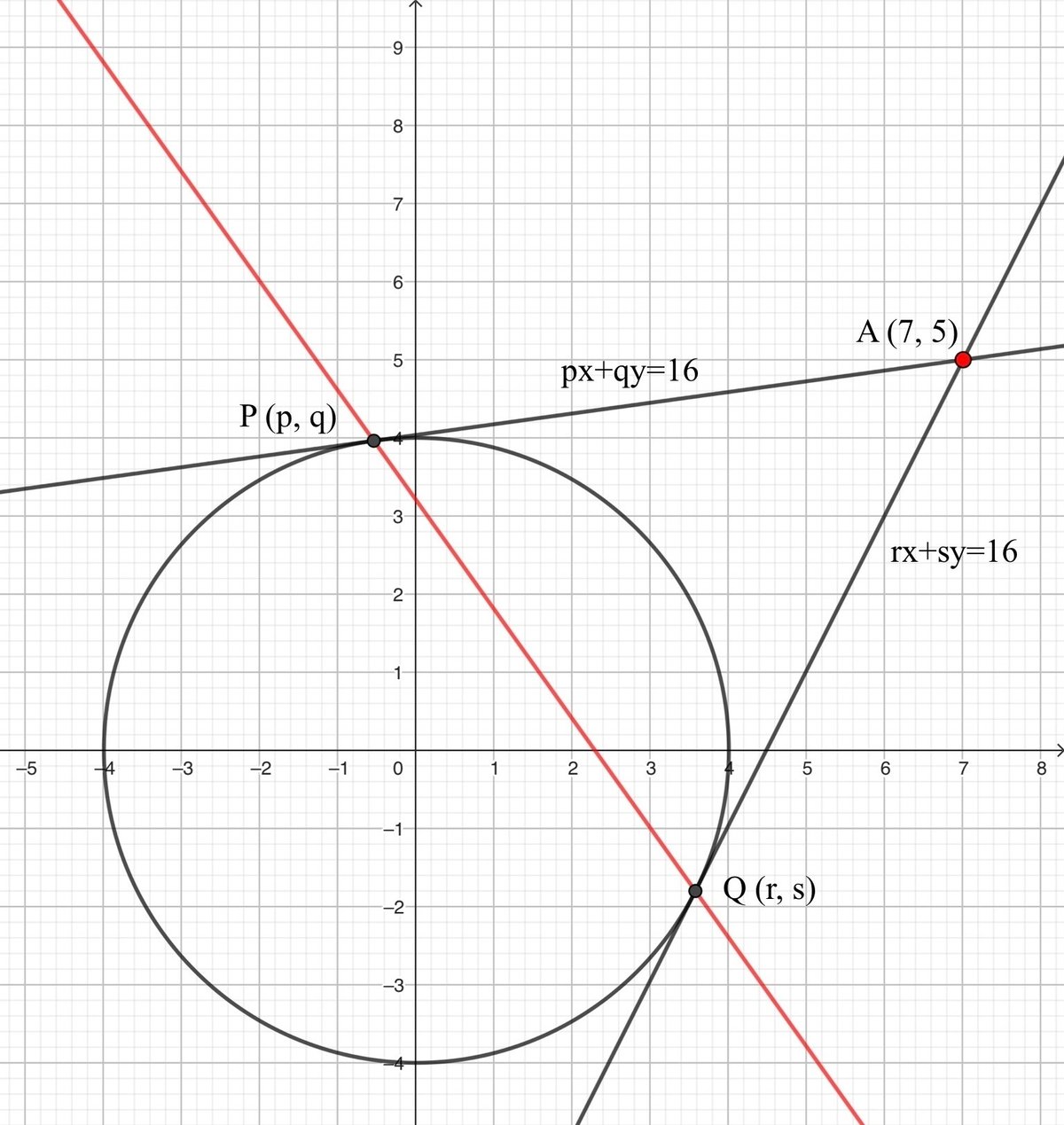
　　接点P, Qの座標を求めるのは大変で、さらにその2点から直線を求める
　　のはもっと大変で……

　　上手いやり方があります
　　接点Pでの接線の方程式は$${px+qy=16}$$、
　　接点Qでの接線の方程式は$${rx+sy=16}$$　であるから
　　これらが点A$${(7,\ 5)}$$を通るので、
　　$${7p+5q=16}$$
　　$${7r+5s=16}$$

　　この2つの式を見て何か思いつかないでしょうか
　　発想の転換です

　　そうこの2式は $${7x+5y=16}$$ に $${(p,\ q)}$$ と $${(r,\ s)}$$ を代入
　　したものなのです

　　さらに発想を転換して直線 $${7x+5y=16}$$ 上に2点P$${(p,\ q)}$$, Q$${(r,\ s)}$$
　　があると見るのはどうでしょう
　　つまり2点P, Qを通る直線の方程式は $${7x+5y=16}$$ なのでした

代入した値（$${7}$$と$${5}$$）がいつの間にか係数として見ている、係数としてみていたもの（$${p}$$と$${q,\ r}$$と$${s}$$）が立場が変わって代入したものになっているところがこの解法の発想の凄いところですね

解(2)

　　(1)より直線STは $${tx+uy=16}$$ です
　　そして点Bは直線 $${7x+5y=16}$$ 上にあるので、$${7t+5u=16}$$
　　が成り立ちます

　　さて $${tx+uy=16}$$……①　と
　　　　 $${7t+5u=16}$$……②　をじっくり見比べてみましょう

　　式②は式①にA$${(7,\ 5)}$$ を代入した形になっています
　　つまり直線ST $${tx+uy=16}$$ 上に点Aがあることにほかならないのです
　　
また、係数（$${7}$$と$${5}$$）が代入する値に立場が変わりましたね

ものの見方は一通りではないので、問題を考えるときは色々な角度から吟味してみて下さい
案外、もとの問題から離れて凄いものが得られるかもしれません