
ベイジアンABテストの利点と活用例(前編)
ベイジアンABテストはABパターンどちらが優れているか確率で表現できる
前回では既存のABテストでは重大な課題があることに言及した
対立仮説が正しいとだけわかるが、有意差が微妙なラインの時に判断が難しい
多重検定があるので何回も柔軟にA/Bテストできない
結論としてABパターンの意思決定にはベイジアンABテストが優れているのだが
今回では「対立仮説が正しいとだけわかるが、有意差が微妙なラインの時に判断が難しい」ときベイジアンABテストがなぜ有用なのかを解説する
そもそも既存ABテストの仮説検定だと帰無仮説が何%正しいかわからない
帰無仮説を棄却するかどうかの二択は判定できるが
特に微妙な差のときやサンプルサイズが小さく有意差の判定が際どいときに
帰無仮説が何%正しいかがわからない
詳しくは前回の記事を参照
仮説検定では帰無仮説が正しいと仮定した上で、
観測されたデータがどの程度「珍しい」ものであるか(p値)を評価する
$$
確率(p値): P(x(得られたデータ) | \theta(母数=帰無仮説))
$$
しかし実際に求めたい確率は
得られたデータから帰無仮説がどれだけ正しいか
$$
求めたい確率: P( \theta(母数=帰無仮説)|x(得られたデータ))
$$
つまり、データが得られた結果を基にして、
帰無仮説が正しいかどうかの確率を計算するのは結果と原因が逆になっているので
求めたい確率を計算することはできない
頻度論的/ベイズ統計学の確率に対する考え方が全く逆
頻度論的統計学の立場ではパラメーター(母数)の値を固定して考えているが
ベイズ統計学の立場からしたらデータを固定して考えているので
確率の考え方が全く逆のアプローチとなっている
頻度論的統計学 :
ある出来事 の相対頻度が試行回数 n を無限大に近づけたときの長期的な頻度この確率は個人の判断に依存しないので客観確率と呼ばれる
$$
客観確率: P(A)= \lim_{n\to \infty} \frac{event count of A in n trials}{n}
$$
この客観確率は下記の $${p_a, p_b}$$のように
全体のサンプルサイズと事象が起こった回数の割り算で求めることができる
# Simulated data: conversion rates and sample sizes
# Version A: control
n_A = 1000 # sample size for A
conversions_A = 120 # number of conversions for A
# Version B: variation
n_B = 1000 # sample size for B
conversions_B = 150 # number of conversions for B
# Frequentist approach
# Compute the conversion rates
p_A = conversions_A / n_A
p_B = conversions_B / n_Bベイズ統計学 :
個人の信念や知識に基づく確率であり、新しい情報や状況によって柔軟に更新される
個々の観測者の見解に依存し、同じ出来事に対して異なる確率を設定することが可能なので主観確率と呼ばれる
$$
主観確率: P(Hypothesis | Data) = \frac{P(Data|Hypothetis) P(Hypothetis)}{P(Data)}
$$
この主観確率は下記の $${p_A, p_B}$$のように
事後分布から確率を生成した
# Bayesian approach
# Prior parameters for the Beta distribution
alpha_prior = 1
beta_prior = 1
# Posterior parameters for A
alpha_post_A = alpha_prior + conversions_A
beta_post_A = beta_prior + n_A - conversions_A
# Posterior parameters for B
alpha_post_B = alpha_prior + conversions_B
beta_post_B = beta_prior + n_B - conversions_B
# Generate samples from the posterior distributions
samples_A = np.random.beta(alpha_post_A, beta_post_A, 10000)
samples_B = np.random.beta(alpha_post_B, beta_post_B, 10000)
# Calculate the probabilities
p_A = np.mean(samples_A)
p_B = np.mean(samples_B)ここでは
二項分布は、特定の成功確率 $${p}$$ に対して、複数回の試行のうちの成功回数がどのように分布するかを表す
→ 尤度関数に使用
ベータ分布は、その成功確率 $${p}$$そのものがどのように分布するかを表す
→ 事前分布に使用
とした
事前分布や事後分布に関して詳しく知りたい方は、下記の記事を参照されたい
(二項ベータ分布の項で詳しく解説している)
主観確率と客観確率については下記
ABテストで求めたい確率はベイズ統計学の主観確率が相性がいい
ABテストで求めたい確率は下記の様であった
$$
求めたい確率: P( \theta(母数=帰無仮説)|x(得られたデータ))
$$
得られたデータを元に母数の確率を計算したいので
下記の主観確率が相性がよく
$$
主観確率: P(Hypothesis | Data(得られたデータ))
$$
ABテストのどちらのパターンがどれくらいの確率で優れているかわかる
※ 補足として既存の古典的な客観確率では帰無仮説を採用すべきかという一つのことがらの信用度を表すことができないことは松下[1960]でこう指摘されている
現在迄の統計の研究の多くは,確率の客観的解釈の許に展開されて来た。
しかし,確率の客観的解釈も常に適切であるとは限らない。
それは客観的解釈というものは, 元来繰返しのきく出来事、つまり一つの過程に対して適応されるものであって、或る一つのことがらが真である確率な どというときにはそのことがらが真のとき1、真でないとき0を与えることの外、意味がないからである。
従って、一つのことがらが成立つことに対する信用度,見込等ということは、そのことがらが確率何々で成立つ等というように表わすことは出来ない。
ベイジアンABテストの実装例
それでは実際にベイジアンABテストを実装していく
今回考えるABテストケースは
KPI :CVR(ユーザー数のうちの契約数)
サンプルサイズ:1000人
CV数:A群120人 B群150人
とする
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
# Simulated data: conversion rates and sample sizes
# Version A: control
n_A = 1000 # sample size for A
conversions_A = 120 # number of conversions for A
# Version B: variation
n_B = 1000 # sample size for B
conversions_B = 150 # number of conversions for B
# Bayesian approach
# Prior parameters for the Beta distribution
alpha_prior = 1
beta_prior = 1
# Posterior parameters for A
alpha_post_A = alpha_prior + conversions_A
beta_post_A = beta_prior + n_A - conversions_A
# Posterior parameters for B
alpha_post_B = alpha_prior + conversions_B
beta_post_B = beta_prior + n_B - conversions_B
# Generate samples from the posterior distributions
samples_A = np.random.beta(alpha_post_A, beta_post_A, 10000)
samples_B = np.random.beta(alpha_post_B, beta_post_B, 10000)
# Calculate the probability that B's conversion rate is greater than A's
prob_B_better_than_A = np.mean(samples_B > samples_A)
# Calculate the expected lift (improvement in conversion rate)
expected_lift = np.mean(samples_B - samples_A)
print(f"Bayesian approach: P(B > A) = {prob_B_better_than_A:.4f}")
print(f"Expected lift (B - A) = {expected_lift:.4f}")
# Plotting the posterior distributions
plt.figure(figsize=(10, 6))
plt.hist(samples_A, bins=50, alpha=0.5, label='Posterior A', color='blue')
plt.hist(samples_B, bins=50, alpha=0.5, label='Posterior B', color='orange')
plt.axvline(np.mean(samples_A), color='blue', linestyle='dashed', linewidth=2, label='Mean A')
plt.axvline(np.mean(samples_B), color='orange', linestyle='dashed', linewidth=2, label='Mean B')
plt.title('Posterior Distributions for Conversion Rates of A and B')
plt.xlabel('Conversion Rate')
plt.ylabel('Density')
plt.legend()
plt.show()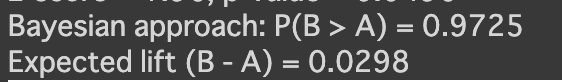

Bayesian approach: P(B > A) = 0.9725
となるので97%の確率でB群が優れていることがわかり
Expected lift (B - A) = 0.0298
から平均で主観確率は約3%B群の方がCVRが高いことがわかった
ちなみに
サンプルサイズ:1000人
CV数:A群120人 B群150人
より
A群の客観確率は0.12%
B群の客観確率は0.15%
なので客観確率でも平均で3%B群の方がCVRが高いので
主観確率と客観確率の結果は一致している
既存のABテストとの比較
参考までに既存のABテストで結果を確認すると下記の様になる
# Frequentist approach
# Compute the conversion rates
p_A = conversions_A / n_A
p_B = conversions_B / n_B
# Compute the pooled conversion rate
p_pooled = (conversions_A + conversions_B) / (n_A + n_B)
# Compute the standard error of the difference in conversion rates
se_diff = np.sqrt(p_pooled * (1 - p_pooled) * (1/n_A + 1/n_B))
# Compute the z-score
z_score = (p_B - p_A) / se_diff
# Compute the p-value
p_value = 2 * (1 - stats.norm.cdf(abs(z_score)))
print(f"Frequentist approach: Conversion rate A = {p_A:.3f}, Conversion rate B = {p_B:.3f}")
print(f"z-score = {z_score:.2f}, p-value = {p_value:.4f}")
有意水準5%にするとサンプルサイズが少ない分僅差なものの有意差がある結果となるが、有意差が僅差な分意思決定に迷ってしまう
そこでベイジアンABテストを実施して下記の様にB群(オレンジ)が明らかにA群(青)より優れていて
その確率は97%であるとわかる
【再掲】

