
ひふみ九九算表(天と地をひっくり返せ!)
ひふみ九九算表というのがあるそうです。
そして、「ひふみ神示」と言うものが、まるで都市伝説のように存在してました。いや~、今の今まで全く知りませんでした。(笑)
日月神示 - Wikipedia http://buff.ly/2giUau6
もう、スゴイ予言をしているようなのですが、今回はそこには全く触れません。気になる方は、WIKIPEDIAへGO!
ひふみ九九算表、見てください。この表の美しさ!!

一目見て、惚れました♪ベタ惚れです♪ヤバすぎます!!
これぞ、まさに「空即是色、色即是空」この世の全てだと思いました!!
皆様に伝わりますでしょうか!
この美しき表の素晴らしさ♪(笑)
まるで数独パズルみたいだ(笑)
そしてこの表を使って、天と地をひっくり返します。
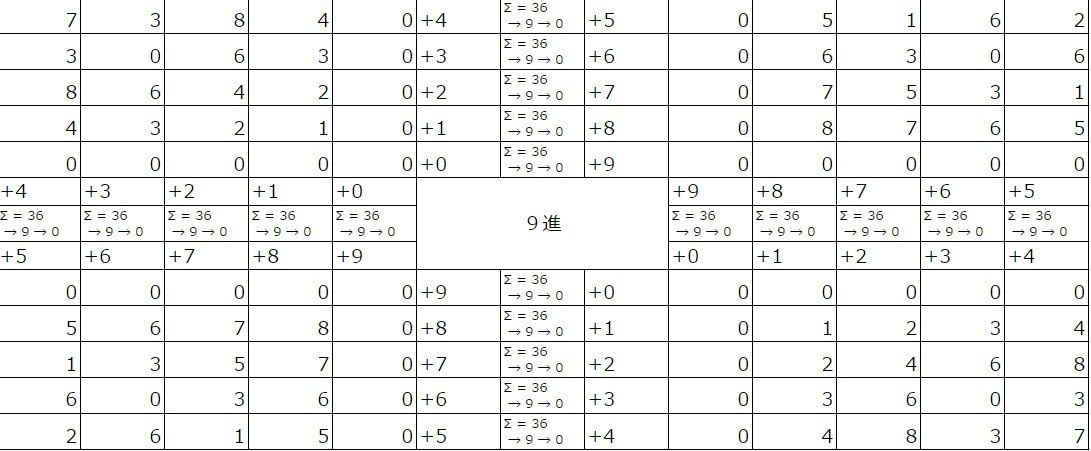
ぱっと見、何が起きたんだ?って感じですね(^-^;
もうこれ、永久ループですは。しかも入れ子構造ですは。3・6・0の辺りなんて円周率を想起させます♪まるでねじれ現象ですは。
もうなにこれ、永続的に繰り返される仕組みを見つけた感じに近い感覚ですよね(笑)
これを十進数で書いてみると

なんだ?規則性なんて有るの?そう思いました?
ですよね。これ、面白いんです実は・・・・
十進数の場合、0が5だったら面白いんですよ。ど真ん中の数字だから面白いんです(笑)
ということで10進数の場合のひふみ九九算表は

これが答えになるでしょう。
ここでも9進数でやった天と地をひっくり返せを

9進数の時よりもよりわかりやすくなったような気がしませんか?
そう感じるのは、私だけでしょうか?
これが宇宙の次元階層だとしたら、あまりにも円環が美しい。
こうなると次に気になるのは、5進数だとどうなるんだ?

ここまで少なくすると円環部分は見えなくなりますね。
気になるのはカミムスビです。9進数のようにゾロ目の数ではありません。
美しい配列は、斜めに交差しているように見えます。
最小値は3進数になるかもしれません。
では、最後にカミムスビである数字6進数では一体どんな表が完成するでしょうか?

6進数になると円環が見えてきます。まだ、この時点では「天と地をひっくり返せ」が可能ですね。

では、最後に残されたのが、3進数。
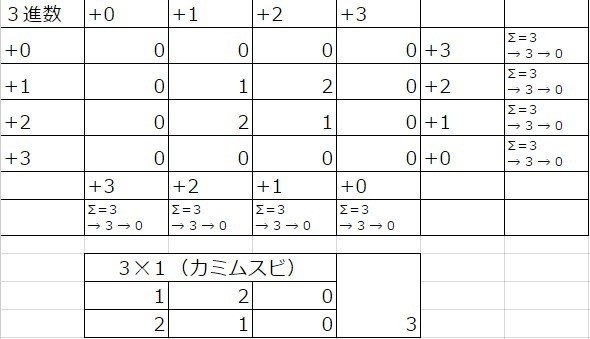
合計とゼロになる数字が同じ値になりました。これ以上少なくすることは不可能です。
これは共に9進数の時に出現していた、折り返し地点の数値と同じですね。
そしてこれは、共に3の倍数でもあります。
何だかとても円周率と深い関わりが有るように感じてなりません。
その円周率は何回目の3.14…なのでしょう。|ふぃろ 【マガジンに来てね♪】|note(ノート) https://note.mu/otspace0715/n/n34dc0342c13b
不思議な数字と言われる「7」これも気になります。
7進数についても追ってみましょう。

7進数になると、また円環がボヤケてしまいます。
しかし、8進数になるとまた円環部分が出現します。
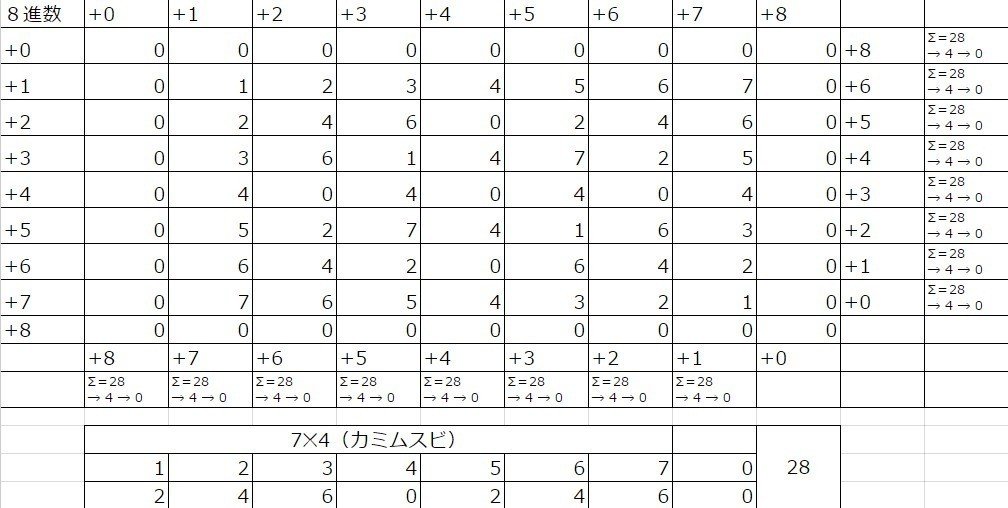
今度は4が0になるということです。
7進数も8進数もカミムスビは、ゾロ目ではありません。
5進数と6進数のカミムスビは、ゾロ目ではありません。
10進数もゾロ目ではありません。11進数とかやるのであれば、5✕11(カミムスビ)になるのかもしれません。合計が55となるので……
9進数のみがカミムスビで6のゾロ目となる最小値ということはわかりました。
4進数もやっておきましょう。2進数はやる必要ないですよね。中央に「1」しか存在しない「0」に囲まれた表なわけですから(^-^;

そして、円環が発生する最小の値は4進数からのようです。ただしやはりゾロ目ではありません。
ここで見えてくる新たな発見は、斜めに6進数の可能性が見えてきました。
0・3・0の繰り返しです。
そして、今発見したのですが、6進数の中にこれも斜めに入っているのですが8進数の円環を見つけます。
0・4・0の繰り返しです。
8進数の中には斜めに、0・5・0・1・0・5・0となっていますので、10進数の一部が現れています。
まるで細胞分裂のようです。
9進数は、0・3・6を繰り返しますので、この部分で切り取りをすると表の中には9つの表が作られているという事になります。
3進数表が9つあると見ることが出来ますし、
この美しいところは、その中の表のマス目が9つ有るということです。
即ち、9進数には、繰り返しと入れ子構造を永久的に拡張し続ける表となっているのです。
それでは最後に本題となりました。9進数のひふみ九九算表で御別れです。
ご静聴ありがとうございました。

この表、最高です♪
ここから先は
いつもサポートありがとうございます♪ 苦情やメッセージなどありましたらご遠慮無く↓へ https://note.mu/otspace0715/message

